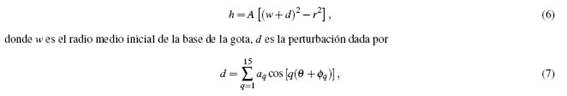I. INTRODUCCIÓN

La motivación de este trabajo se basa en los experimentos realizados por Domínguez et al. [¹], en los que se deposita una gota sobre el centro de una superficie circular sólida, cuya temperatura decrece con el radio. Este gradiente de temperatura en el sustrato induce un esfuerzo de Marangoni en la interfaz líquido-aire, que desplaza el líquido radialmente hacia afuera. Este tipo de trabajos son cruciales en la práctica, porque permite entender la dinámica alrededor del desplazamiento de pequeños volúmenes de fluidos [^{2, 3}]. Algunas áreas de investigación en la que se aplica ampliamente son la microfluídica, modelos de superficies, etc [4, 5]. La evidencia experimental mostró que el flujo de líquido hacia la periferia hace que la gota evolucione hasta adoptar la forma de un anillo cuyo radio crece con el tiempo. Este anillo experimenta una etapa inicial estable en la que el flujo mantiene la simetría axial, la cual fue estudiada en la Ref. [1] mediante simulaciones numéricas. Cuando el anillo líquido alcanza un radio adimensional de aproximadamente 3, la línea de contacto del anillo se vuelve inestable, mostrando ondulaciones suaves que crecen con el tiempo y eventualmente se vuelven largas protuberancias llamadas “dedos”. El análisis de Fourier de la línea de contacto realizado en Ref. [¹], muestra que conforme pasa el tiempo, crece el número de onda del modo dominante. Esto representa una gran diferencia con flujos de gravedad o centrífugos, donde la inestabilidad desarrolla una longitud de onda que domina el espectro y que permanece constante en el tiempo [^6-8]. En el presente artículo, se muestran simulaciones numéricas de este flujo buscando replicar numéricamente los resultados experimentales obtenidos por Domínguez et al., y alcanzar un mejor entendimiento de la etapa inestable. El texto está organizado de la siguiente forma. En la sección II se explicitan las hipótesis adoptadas que permiten derivar la ecuación de gobierno para el espesor del líquido. En la sección III se muestran los resultados numéricos, donde se analiza la evolución de la línea de contacto al introducir perturbaciones al perfil axisimétrico de una gota. Finalmente, en la sección IV se discuten los resultados obtenidos comparándolos con la evidencia experimental y se presentan las conclusiones.

II. EL PROBLEMA Y SUS ECUACIONES

Se tiene un substrato circular y horizontal con un gradiente térmico axisimétrico dado por

Notar que, gracias a las escalas utilizadas, esta ecuación resulta libre de parámetros.

La ecuación (5) se discretizó y resolvió mediante el método de elementos finitos. Se empleó un esquema de diferenciación inversa (BDF) con paso de tiempo adaptativo, y se utilizó el solver "MUltifrontal Massively Parallel sparse direct Solver"(MUMPS) precondicionado mediante un algoritmo de multigrid estándar [12]. Para el error relativo, definido por una norma euclidiana ponderada para dos pasos de iteración sucesivos, se determinó como criterio de convergencia un valor de 10−3.

FIG. 1: Perfil inicial característico, dado por las ecuaciones (6, 7).

III. RESULTADOS

Se resolvió numéricamente la ec. (5) asumiendo como forma inicial de la gota un paraboloide de revolución con línea de contacto perturbada (ver Fig. 1), descrito por la ecuación

donde θ es el ángulo azimutal, q es el número de onda, y aq y φq son la amplitud inicial y fase de cada modo, respectivamente. El valor de A es elegido de modo que R hdV = 1. Dado que el líquido moja completamente al sustrato, se asumió también que este está cubierto por una película líquida uniforme de espesor hc =10−4, lo que permite evitar la divergencia del esfuerzo en la línea de contacto [13, 14]. Con el objeto de reproducir los resultados presentados en [1], se hizo una simulación combinando modos normales tomando q = 1. . . 15, amplitudes aq aleatorias distribuidas normalmente con media nula y desvío estándar 0.04, fases φq aleatorias uniformemente distribuidas en [0,2π), y w = 1, 8. El resultado a un dado instante se puede ver en la Fig. 2 (comparar con Fig. 2 (d) de la Ref. [1]). Para cada instante t se halló el contorno (definido arbitrariamente como la línea en la que h = 10hc), y de cada contorno se calculó desde su centro el radio medio < r > y desvío estándar SD. En la Fig. 3 se muestra SD en función de < r >, y puede verse una disminución inicial hasta aproximadamente < r >= 2.2, a partir de lo cual el desvío aumenta. Por otra parte, se realizaron 15 simulaciones cada una con sólo un modo normal presente con número de onda q, con q desde 1 a 15, todas con w = 1.8 y aq = 0.09, con el objetivo de estudiar la evolución de cada modo individualmente. En la Fig. 4 se puede ver la amplitud del espectro de Fourier de los contornos en función de t para cada una de dichas corridas numéricas (se muestran resultados sólo para q < 10 para una mejor visualización de los resultados). En cada una de las 15 simulaciones se observa que la amplitud del único modo normal presente disminuye inicialmente, y a partir de cierto valor de t (y por lo tanto de < r >) empieza a crecer. Dicho valor de t (y de < r >) es ligeramente distinto para cada valor de q. También se puede observar que a tiempos mayores hay una tendencia a que el q del modo con mayor amplitud sea cada vez más grande.

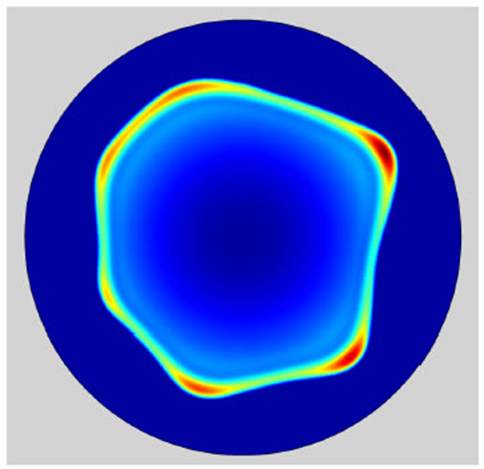
FIG. 2: Solución numérica de la ec. (5) a un dado instante, con 15 modos normales cada uno con amplitudes iniciales y fases aleatorios. La escala de color indica con rojo (azul) el mayor (menor) espesor h.

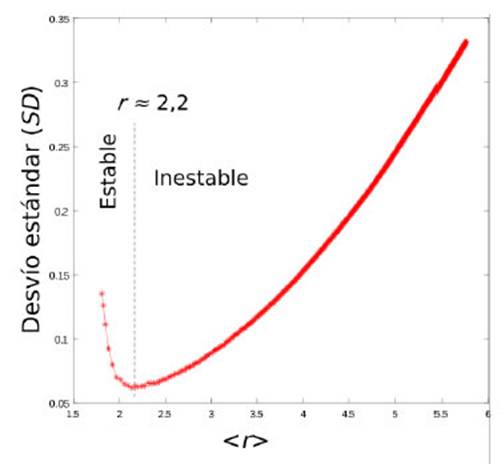
FIG. 3: Desvío estándar del radio en función del radio medio del contorno de la solución numérica. Se observa un mínimo de SD en< r >≈ 2.2, indicando la transición de la etapa estable a la inestable.

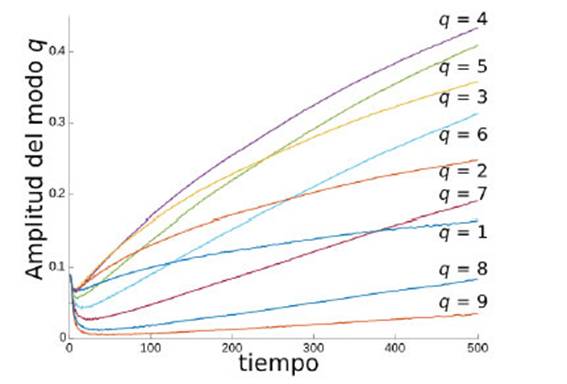
FIG. 4: Evolución temporal de la amplitud de la perturbación en las corridas numéricas en las que sólo hay un modo normal presente.

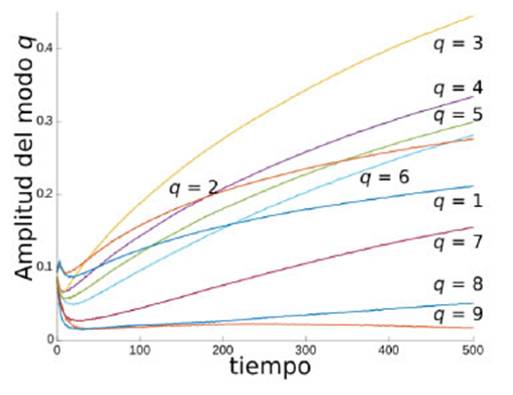
FIG. 5: Evolución temporal de la amplitud de cada modo normal en una corrida numérica en las que hay presentes 15 modos normales.

Finalmente, para evaluar la posibilidad de interacción entre modos normales, se realizó una simulación con los 15 modos presentes simultáneamente, todos con la misma amplitud inicial de la perturbación aq = 0.09, fases aleatorias, y radio medio inicial w = 1.8. En la Fig. 5 se muestra la amplitud del espectro de Fourier de cada modo del contorno de esta solución numérica en función del tiempo. Si bien con algunas diferencias, al igual que en la Fig. 4, la amplitud de cada modo disminuye al inicio y luego crece, y a tiempos grandes el q del modo dominante es cada vez mayor. IV. DISCUSIÓN Y CONCLUSIONES La conclusión principal es que las coincidencias entre los resultados numéricos y los experimentales evidencian que el modelo, expresado en la ecuación (5), incluye la física relevante. Sin embargo, se deben realizar más análisis para mejorar la manera de introducir perturbaciones. También debe estudiarse en qué medida los detalles del perfil inicial (como por ejemplo el radio inicial w) modifican el valor numérico del radio de transición entre las etapas estable e inestable. Se obtuvieron coincidencias cualitativas entre soluciones numéricas y los experimentos reportados en la Ref. [1], que enumeramos a continuación. 1) Una comparación visual de la Fig. 2 con las Figs. 2 (c) y (d) de la Ref. [1] muestra que sus contornos tienen un aspecto muy similar. Esta es una apreciación subjetiva, pero debe hacerse porque, si no fuera así, significaría que algunas de las hipótesis adoptadas para arribar a la ec. (5) son incorrectas. 2) Al igual que en los experimentos, las soluciones numéricas presentan una primera etapa estable, evidenciada por la disminución del desvío estándar del radio, seguida por una etapa inestable, en la que el desvío aumenta. Cabe destacar que aquí se optó por seguir la evolución del desvío estándar del radio para detectar la estabilidad o inestabilidad ya que esa fue la manera en que se lo hizo en [1]. 3) El radio obtenido aquí en el que ocurre la transición entre estas etapas es aproximadamente 2.2, cercano pero ligeramente inferior al reportado experimentalmente, que es aproximadamente 3 (con una incertidumbre de 0.6). Notar que el valor obtenido aquí puede depender de los detalles del perfil inicial, tales como el radio de su base w y su forma. 4) De las Figs. 4 y 5 se observa que el número de onda del modo dominante crece con el tiempo, al igual que en los experimentos. Estos resultados concuerdan tanto para las soluciones numéricas con un único modo como para aquella con varios modos presentes simultáneamente. A pesar de que en la Ref. [1] el líquido utilizado fue PDMS, cuya viscosidad depende de T, aquí supusimos, al igual que en Refs. [1, 15] (en [15] también se utilizó PDMS), que la viscosidad es constante.

Esto equivale a asumir a priori la hipótesis de que en los experimentos, los efectos de la dependencia de µ con T son de poca importancia comparados con los que genera la variación del coeficiente de tensión superficial γ con T (como efectivamente se concluye del excelente acuerdo encontrado en la Ref. [1] entre las velocidades de avance de la línea de contacto calculadas con un modelo bidimensional y las experimentales). Dicha hipótesis se ve respaldada a a posteriori por las coincidencias comentadas en el párrafo anterior entre nuestros resultados numéricos y los experimentales reportados en Ref. [1].

Por otra parte, las diferencias entre las Figs. 4 y 5 evidencian que existen interacciones entre modos. Si estas no existieran, la evolución de un dado modo normal sería la misma independientemente de la presencia de otros modos con diferente número de onda. En los experimentos las perturbaciones pueden estar presentes en todo momento debido a imperfecciones en el sustrato, en el gradiente térmico, impurezas en el líquido, etc. Por otra parte, en las simulaciones presentadas aquí, el sistema es perturbado sólo en el instante inicial, por lo que el perfil inicial debe ser suficientemente perturbado como para que conforme pase el tiempo la perturbación sea visible, tal y como ocurre experimentalmente.