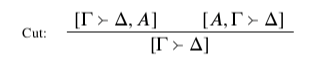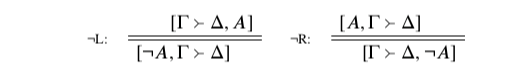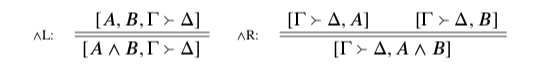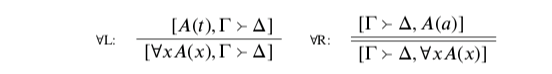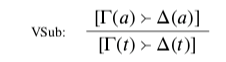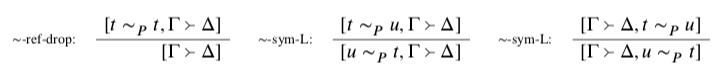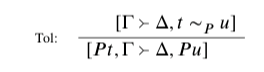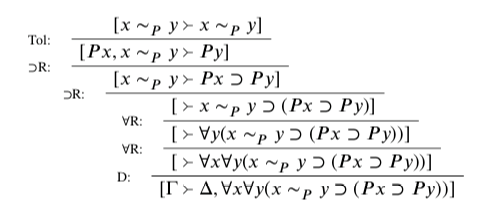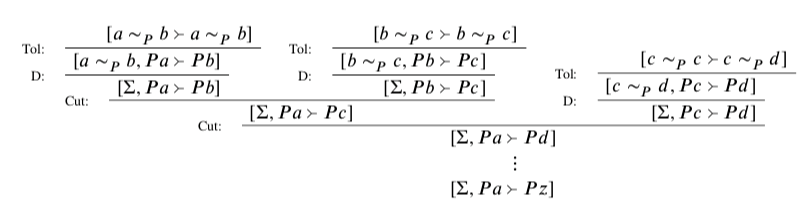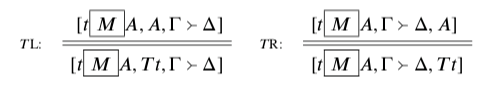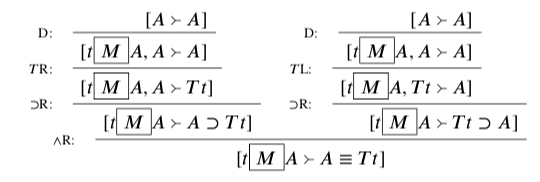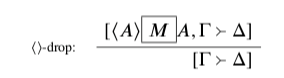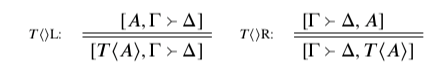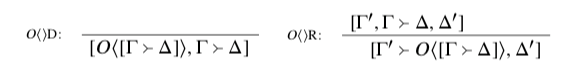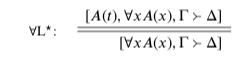Positions and bounds

The approach Uncut takes to meaning is centered on the speech acts of assertion and denial, and certain norms that govern collections of these acts. I’ll refer to a collection of assertions and denials as a position, and talk of positions as being in bounds or out of bounds.

These bounds are understood as a social kind: they are created and sustained by the place they occupy in our practices. As is usual for social kinds, understanding what it is for a position to be in or out of bounds needs to start from understanding what it is to treat a position as in or out of bounds. (Compare: to explain what it is to be royalty, start from what it is to treat someone as royalty.) Uncut and Ripley (^2017a) go into more depth about this; here I’ll just sketch the rough idea. Some positions simply don’t fit together. For example, a position that asserts and denies the very same thing doesn’t add up. A position that asserts ‘Melbourne is bigger than Canberra’ and ‘Canberra is bigger than Darwin’ while denying ‘Melbourne is bigger than Darwin’ also doesn’t add up.

If someone seems to have adopted a position like this, we might look for some other way to interpret what they’ve said, so that they didn’t really adopt the position. (Maybe they meant ‘bigger’ in terms of population size in some of their utterances, and in terms of font size on a particular map in others.) In the course of looking for such an interpretation, we might ask them for clarification (‘A minute ago I thought you said x. But now you seem to be saying y. What’s up?’). Or, rather than look for an interpretation that works, we might simply dismiss them as talking crap, as not a serious interlocutor. All of these kinds of responses—reinterpretation, asking for clarification, dismissal—are enforcement behaviours important to this social kind. Some positions are taken seriously as the kind of thing someone might mean; others are not. This taking seriously or not is the key activity we engage in to establish the bounds. ²

Admissible & derivable rules

As a proof system, BC is not terribly interesting. But it is already enough to develop a key distinction: the distinction between admissible rules and derivable rules. A rule is admissible in a calculus iff each instance of the rule meets the following condition: if all the premises of the instance are derivable in the calculus, then the conclusion of that instance is also derivable in the calculus.

Figure 2 contains two examples of rules that are admissible in BC: DId (diluted identity) and Swap. To see that they are admissible, start by noting that a position [Γ ⇒ Δ] is derivable in BC iff Γ∩Δ≠∅; BC derives all and only the positions whose assertions and denials overlap. But the conclusion of DId always meets this condition; and if the premise of an instance of Swap meets this condition then so does the conclusion. So both rules are admissible in BC.

Figure 2 DId and Swap 

For a rule to be derivable in a calculus, each instance of the rule must meet a more stringent condition: that if all the premises of the instance are added to the calculus as initial positions, then the conclusion of the instance can be derived in this expanded calculus. DId is not only admissible in BC, but also derivable. (Indeed, any zero-premise rule like DId is admissible iff it is derivable.) But Swap, while admissible, is not derivable in BC. For example, there is an instance of Swap that moves from [p⇒q] to [q⇒p]. But if we add [p⇒q] to BC as a new initial position, there is no derivation in the resulting calculus of [q⇒p]. Rules like this that are admissible but not derivable for a calculus are called merely admissible.

When we add more rules to a calculus, we can sometimes make (merely) admissible rules become inadmissible. We saw an example of this already, in seeing that Swap is not derivable in BC. But in fact, this can happen to any rule R that is merely admissible in a calculus: there is always some way to add rules to the calculus to reach a new calculus for which R is not admissible at all. This can never happen, though with derivable rules: adding to a calculus will never make a derivable rule underivable. This is because derivability, in its definition, already took potential additions into account.

Now, the proof system I am building towards in Uncut is nothing like a complete theory of the bounds. That would be far too much to ask; it would be a complete theory of the meaning of every word in our language. I have no commitment to such a thing being possible even in principle; I certainly am not about to try it. ⁶ The proof systems I give are partial theories of the bounds. If a rule is derivable in the calculi I endorse, then it will remain derivable no matter how these calculi are extended; I am surely committed to the bounds being closed under any such rule. But—and this is why the distinction matters—the same is not true for merely admissible rules. A rule might be merely admissible in one, or even all, of the calculi I endorse, without this carrying any commitment on my part to the bounds being closed under that rule. Its mere admissibility might just be a result of the incompleteness of my theory: there might be counterexamples that my theory is not rich enough to show to be counterexamples.

Indeed, this is just the status that Swap has wrt BC. BC does not have the resources to identify any counterexamples to Swap; and the bounds really do (so I claim) obey all the rules of BC. But nonetheless, the bounds do not obey Swap. It is just that the counterexamples to Swap all turn on the behaviour of particular vocabulary, vocabulary that BC takes no account of.

Cut

Time to look at the rule of cut. I’ll work with the rule in this form: ⁷

Cut’s status in BC is just the same as Swap’s: it is merely admissible. So everything I’ve said so far is compatible with cut’s having counterexamples that turn on the behaviour of particular vocabulary, just like Swap does. Indeed, I think this is exactly the case. The only difference is that for Swap, we can already find such vocabulary among the UFO vocabulary, whereas for cut we must look outside.

But before we get to that vocabulary, it’s worth a look at cut directly in its own right, to see what constraints on the bounds it encodes. After all, Id and D follow directly from the picture in play of what the bounds are and how they work; if cut were to follow from this picture as well, then my claim that BC exhausts the vocabulary-independent constraints on the bounds would fail, and there would be no room for any counterexamples.

So what does cut say, in terms of the bounds? It says that if the positions [Γ⇒Δ,A]and [A,Γ⇒Δ] are both out of bounds, then we can forget all about A: [Γ⇒Δ] is out of bounds on its own. That is, if a position [Γ⇒Δ] rules out in-bounds asserting some claim A, and it also rules out in-bounds denying that same A, then the position itself is already out of bounds, even if it doesn’t say anything about A at all. Contrapositively, we can see cut as an extensibility claim: if a position [Γ⇒Δ] is in bounds, then one of [Γ⇒Δ,A]and [A,Γ⇒Δ] must be too: there must be some in-bounds way to extend [Γ⇒Δ]with A, either by denying it or by asserting it.

At this point, we have no particular reason to think that this doesn’t hold, but we also have no particular reason to think that it does. Why couldn’t it be the case that taking up some position [Γ⇒Δ]rules out taking any stand on A, and yet [Γ⇒Δ] is in bounds? Perhaps the bounds simply require us not to take any stand on A. I’m not yet claiming there are such examples, although I will be soon. Rather, I’m claiming that we have no reason to rule out such examples in advance. Whether this kind of extensibility constraint holds is a matter of the global organization of the bounds; it remains to be seen how that shakes out.

UFO Vocabulary

Meanings of particular pieces of vocabulary are to be given as conditions on the in-bounds assertibility and deniability of sentences involving that vocabulary. Before we get to the particularly paradoxical vocabulary, I’ll start by giving meanings for the UFO vocabulary. This helps in two ways: it gives an example of how this kind of approach to meanings works, and it also allows us to examine interactions between paradox-prone vocabulary on the one hand and the UFO vocabulary on the other.

Here, I’ll just give meanings for negation ¬, conjunction ∧, and the universal quantifier ∀. Other UFO vocabulary (except for equality) can be understood as defined from this stock in the familiar way. ⁸

Negation, I claim, is for swapping the roles of assertion and denial. Asserting ¬A amounts to the same, as far as the bounds are concerned, as denying A; and denying ¬A amounts to the same, as far as the bounds are concerned, as asserting A. This is not an uncontentious theory of negation, of course. But it is a familiar, classically-flavoured one. If there is anything surprising or unfamiliar about it, it is the bounds-based way of expressing this idea about negation, not the idea itself.

This idea finds expression in a pair of double-line rules:

The double line should be understood as an ‘if and only if’; in each rule, the position above the line is out of bounds iff the position below the line is as well. These rules merely encode in symbolic form the theory of negation’s meaning floated above: ¬L tells us when ¬A is assertible (namely, iff A is deniable); and ¬R tells us when ¬A is deniable (namely, iff A is assertible).

On to conjunction. Asserting a conjunction A∧B amounts to the same, as far as the bounds are concerned, as asserting both A and B: the single act is in bounds iff the pair of acts is. And denying a conjunction A∧B is out of bounds iff denying A and denying B are both out of bounds. (A conjunction is undeniable iff both conjuncts are.) This is not an uncontentious theory of conjunction’s meaning (although conjunction in general is less contentious than negation), but it is again a completely standard one, apart perhaps from the bounds-based idiom in which it is expressed.

This theory finds expression in another pair of double-line rules:

The double line again should be read as ‘if and only if’. ∧R is a two-premise double-line rule: this should be read as allowing the bottom position to be derived from the pair of top positions, and as allowing either top position to be derived freely from the bottom position. It thus amounts to ‘both premises iff the conclusion’, which is what’s needed.

The universal quantifier is slightly different from negation and conjunction, in the following way: I’m not here going to give you a full ‘if and only if’ statement of its assertibility conditions. Rather, I’m going to say things I take to be true about the meaning of the universal quantifier, without claiming to have thereby given an exhaustive theory of its meaning. This is, quite frankly, because I don’t know how to give an exhaustive theory of its meaning. Fortunately, though, none is required for my project. At the very least, the following holds: if it is out of bounds to assert A(t) for any term (t), then it must be out of bounds to assert ∀xA(x). Deniability conditions can be pinned down more fully: ∀xA(x) is out of bounds to deny iff A(y) is out of bounds to deny for some variable a in a position that does not otherwise mention a. (This idea makes the most sense with one extra rule, to make sure that variables behave like variables; that’s on its way.)

This leads us to the following rules:

Note that ∀L is only a single-line rule; this fits with the one-way conditional claim about the assertion conditions of ∀ sentences. ⁹ The rule ∀R should be understood as having a side condition: it may only be applied when the variable a does not occur free in Γ ∪Δ. If the position [Γ⇒Δ]already says things about a, then ruling out denial of A(a) should not suffice for ruling out denial of ∀xA(x); the denial of A(a) might be ruled for for reasons that have to do with a specifically. But if [Γ⇒Δ] says nothing at all about a, and still manages to make A(a) undeniable, then this must be for reasons that have nothing at all to do with a; the position must also make ∀xA(x) undeniable.

In order to state the deniability conditions for A, I made use of the notion of a variable. The key idea for variables is that they are mere placeholders, with no special assumptions made about them. So if a position involving a variable is out of bounds, then the corresponding position using any term in place of the variable must be out of bounds as well. ¹⁰ That is, we have the rule VSub:

In this rule, a should be understood as a variable with all of its free occurrences indicated, and t is an arbitrary term. As a result, there will be no free as left in the conclusion position. Sequent systems are often designed so that VSub is merely admissible, but recall that I’m trying to avoid appeal to merely admissible rules. To be sure that variables behave like mere placeholders, then, even after new rules are added later, we may as well impose VSub directly.

That, then, gives such a theory as I have to offer here of the meanings of the UFO vocabulary. When the rules from this section are added to BC, we arrive at a calculus I’ll call CL. This calculus is sound and complete for first-order classical logic without equality. ¹¹

That is, a position is derivable in iff it is classically valid. The ‘if’ direction of this claim is not particularly important, except to reassure you that I have not gone too far. (And it only works for this purpose if you don’t think classical logic itself goes too far!) But the ‘only if’ direction gives a sense in which Uncut holds that classical logic is ‘correct’: if classical logic can show that Γ ⊢Δ, then it is out of bounds to assert everything in Γ while denying everything in Δ. ¹²

Checking in with cut

Since CL’ derives a position iff that position is a classically valid argument, it follows that cut is admissible in CL’. (Classical validity is surely closed under cut, and CL’ simply determines classical validity, so what CL’ determines is closed under cut.) Cut is not, however, derivable in CL’.

Recall the earlier discussion of admissible and derivable rules: cut’s admissibility in CL’ does not guarantee that it will remain admissible when additional rules are added. Note what’s happened to Swap. While it was admissible in BC, it is not admissible in CL’; the addition of the extra rules governing the UFO vocabulary has changed things. For example, [p∧q⇒p] is derivable in CL’, but [p⇒p∧q] is not. Since Swap was merely admissible in BC, this is the kind of thing that can happen.

Since cut too was merely admissible in BC, the same thing might have happened to cut in CL’. But it did not. Still, cut remains merely admissible in CL’. So it is possible that, as we add further rules to capture more of how the bounds behave, cut will go the way of Swap. In CL’, nothing breaks cut, but still nothing prevents it being broken; it merely happens to work.

Vague predicates

When it comes to giving a theory of the meaning of vague predicates, I won’t try to give anything like a full theory of the meaning of any particular predicate. Rather, I’ll attempt to capture the sense in which vague predicates are tolerant, or insensitive to small-enough differences. Tolerance is the place to focus for two reasons. First, it is what vague predicates have in common, what makes them vague, so we can get something like a general theory of vague predicates by focusing here. Second, it is what gives rise to the paradoxical behaviour of vague predicates. So if we can capture the sense in which vague predicates are tolerant without problematic conclusions following, we have done enough.

Tolerance for a vague predicate P says that if two things are similar enough in the right ways, then if one of them is P so too is the other. What ‘similar enough in the right ways’ amounts to differs wildly from predicate to predicate, as well as from context to context; this variation is no part of what Uncut considers. So I will simply assume that, for each predicate P, there is a binary relation ∼ _p expressing this notion. ¹³ Moreover, I’ll assume that ∼ _p genuinely is a similarity predicate: that is, that it is reflexive and symmetric, in the sense that the bounds obey the following rules:

∼-ref-drop says that if a position asserting t ∼ _p t is out of bounds, this can’t be because it asserts t ∼ _p t; it must be out of bounds even without this assertion. This is a way to hold t ∼ _p t completely innocent. ¹⁴ The two ∼ sym rules simply say that asserting or denying a similarity claim amounts to the same as asserting or denying (respectively) its flipped-around version.

Tolerance itself is captured in the following rule:

Read top to bottom, this says that when t ∼ _p u is undeniable, then it’s out of bounds to assert Pt and deny Pu. To assert Pt and deny Pu, after all, would require denying (at least implicitly) that t and u are similar enough to trigger a tolerance requirement.

This rule on its own involves none of the UFO vocabulary: tolerance can be seen as a constraint relating P to ∼ _p directly. This is as it should be: while statements of tolerance in sentence form require bits of UFO vocabulary, in the end attempts to ‘salvage’ tolerance by fiddling with the UFO vocabulary end up making tolerance mean something other than what it should. ¹⁵ Tolerance, at its heart, doesn’t really involve UFO vocabulary.

Such vocabulary is useful at best in making it explicit in sentence form. And by adding the Tol rule to CL’, it becomes possible to see how this explicitation can work. ¹⁶ Consider the following derivation: ¹⁷

Given tolerance, together with the going theory of the UFO vocabulary and the constraints on the bounds encoded in BC, any position denying ∀x∀y (x∼p y ⊃ (Px ⊃Py)) is thus out of bounds. This is not tolerance itself, but a reflection of it visible via the UFO vocabulary, given the rules in play. Tolerance remains as expressed in Tol: a direct connection between P and ∼ _p .

Checking in with cut

Let CLV’ be plus the rules and the Tol rule. This tells us more about the bounds than CL’ alone; it now encodes tolerance for vague predicates as well. So a natural question arises: what happens with the sorites paradox?

Let’s set one up and see. Consider a sorites series a, b, c, …, y, z of objects, each P-similar to its neighbors, but such that a is P and z is not. Let Σ be the set of similarity claims {a∼ p b,b∼p c, …, y ∼p z}. Now, consider the following non-derivation:

This is a non-derivation because it features repeated use of cut, which is no rule of CLV’. But the only other moves it involves are Id, D, and Tol. So if cut is admissible in CLV’, then the position [Σ,Pa⇒Pz] is derivable in CLV’, and so must be out of bounds if CLV’ is correct. But this position had better not be out of bounds! It simply captures the soritical setup: all these things are similar to their neighbors, and a is P, and z is not. If CLV’ declares [Σ,Pa⇒Pz] to be out of bounds, it has fallen victim to the sorites paradox. So it had better not do this. But then it had better not admit cut.

Fortunately, it does not. To see this, it suffices to show that [Σ,Pa⇒Pz] is underivable; and to see this, the easiest way is to use a bit of model theory. Before I sketch the idea, though, it’s important to remark on just how philosophically unimportant these models are. They certainly are not involved in any way in the going theory of meaning. I am simply using the models as a convenient way to prove that a certain position isn’t derivable in CLV’. And CLV’ isn’t even itself all that philosophically important; it is, I think, correct in its claims about the bounds, but it certainly does not exhaust the truth about them. Moreover, there is nothing particularly important about stopping exactly where CLV’ happens to: no special status attaches to those positions whose out-of-boundsness can be established in CLV’, as opposed to other out-of-bounds positions that are out of bounds for some other reason. So it would be a mistake to interpret models for CLV’ as telling us much at all about meaning; they are a mere technical auxiliary to a partial theory of what really matters.

The needed models are quite simple: three-valued models on the so-called strong Kleene scheme, with a few additional constraints on atomic valuations. These models assign to each sentence a value from the set {0,1/2,1}; I won’t here rehearse the recursive clauses for complex sentences, but they are straightforward and can be found, for example, in Priest (²⁰⁰⁸) and Beall and Fraassen (²⁰⁰³). The needed extra constraints are: 1) that t ∼ _p t always takes value 1; 2) that t ∼ _p u and u ∼ _p t always take the same value as each other; and 3) that whenever a valuation assigns t ∼ _p u a value greater than 0, then the values it assigns to Pt and Pu cannot differ by 1.

Three-valued models are reasonably familiar in the study of nonclassical logics, but less so in the study of classical logics. (Not unknown, though: see for example Girard (¹⁹⁸⁷, Ch. 3), which works with three-valued ‘Schütte valuations’.) The key is in the notion of countermodel: one of these three-valued models is a countermodel to a position [Γ⇒Δ] iff it assigns 1 to everything in Γ and 0 to everything in Δ. With this notion of countermodel in mind, it is not hard to show that CLV’ is sound: no position derivable in CLV’ has a countermodel. The three-valued models alone take care of CL’; the additional restrictions on atomics are what we need for the additional rules present in CLV’.

But now to show that [Σ,Pa⇒Pz] is not derivable in CLV’, it suffices to produce a countermodel to this position; since CLV’ is sound, it does not derive anything that has a countermodel. ¹⁸ Such countermodels are easy to come by. Since every sentence in Σ must have value 1 on any such countermodel, it follows that no adjacent claims in Pa,Pb,…,Pz can differ in value by 1. But still Pa can have value 1 and Pz value 0, as is needed; while none of the 25 steps along the way can leap from 1 to 0 or 0 to 1, none needs to; there is always the value 1/2 to be taken along the way.

To bring the discussion of CLV’ to a close, then: we have seen that [Σ,Pa⇒Pz] would be derivable if cut were admissible in CLV’; and we have seen that it is not derivable. So we can conclude that cut is not admissible in CLV’. Moreover, it could not be correctly added: [Σ,Pa⇒Pz] shouldn’t be reckoned out of bounds. Cut, in CLV’, goes the way that Swap went in CL’. While these rules may be merely admissible in weaker calculi, once we add to our theory of the bounds we can find counterexamples to them.

Truth

Another important predicate for paradoxes is the truth predicate T, and its interactions with names for sentences. I suppose a few things about our language here. First, there is a ‘means that’ nective M ; this forms a sentence from a term and a sentence, allowing us to have t M A saying that t means that A. With this in hand, we have two double-line truth rules:

Once a position asserts that t means that A, then any constraints that position is subject to around asserting or denying A transfer to the claim that t is true; and any contraints that position is subject to around asserting or denying that t is true transfer to A.

With these rules in hand, we can derive something like Tarski’s T-scheme: ¹⁹

That is, it is out of bounds to assert that t means that A while denying Tt≡A.

In much of the literature on semantic paradoxes, each sentence A is given a canonical name ⟨A⟩. If such canonical names are present in the language here (and why not?), then they can be captured with the following rule:

Like the ∼-ref-drop rule in CLV’, this rule ensures that asserting that ⟨A⟩ means that A is always held totally innocent by the bounds: if a position asserting ⟨A⟩ M A is out of bounds, it can’t be because it makes that assertion. It would’ve been out of bounds anyhow.

With this rule in hand, it becomes possible to derive the following rules, which might be more familiar. ²⁰

That much, then, gives us a pretty straightforward, naive theory of truth. The claim that A is true, at least when made with A’s canonical name, does not differ at all boundswise from A itself. Each is assertible iff the other is and deniable iff the other is.

This setup, though, allows for a wide range of paradoxes to be formulated. Without some extra story about canonical names, for example, there is no reason we can’t have a sentence that contains its own canonical name. For example, we might have a sentence ¬Tt, where t is the canonical name for ¬Tt itself. Let λ be such a sentence; that is, λ is ¬T⟨λ⟩. This is a liar paradox: a sentence that says of itself that it is not true. Similarly, we might have a sentence Tu⊃A, where u is the canonical name for Tu⊃A itself. Let κ_A be such a sentence; that is, κ_A is T⟨κ_A⟩⊃A. This is a curry paradox (with consequent A): a sentence that says of itself that if it is true, then A. (This is not to mention paradoxical pairs, triples, or other loops, or ‘contingent’ paradoxes that can be formed from terms other than canonical names by using the M nective, but I’ll leave those things for the book.)

Checking in on cut

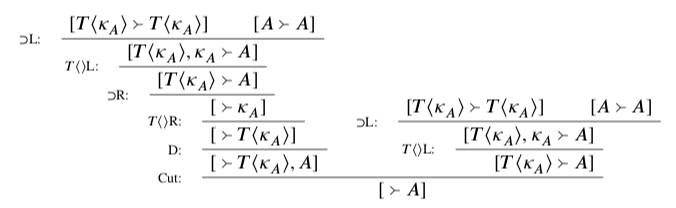
Let CLT’ be CL’ plus the T rules and ⟨⟩-drop. ²¹ To see what happens with paradoxical sentences, consider the following non-derivation.

This is a non-derivation only because of the step of cut; everything else checks out in CLT’. ²²

So if cut is admissible in CLT’, then [Γ⇒Δ] is derivable in CLT’. But this would be a bad result: that’s an arbitrary position! CLT’, on its intended interpretation, would be saying that every position is out of bounds. It had better not do this; so it had better not admit cut.

Similarly, recalling that κ_A is the sentence T⟨κ_A⟩⊃A, we have the following non-derivation to consider:

Again, this is a non-derivation only because of the cut. So if cut is admissible in CLT’, then [⇒A] is out of bounds. But this is bad: A here is arbitrary! CLT’, on its intended interpretation, would be saying that no sentence is in-bounds deniable. It had better not do this; so again, it had better not admit cut.

To see that all is well, that CLT’ indeed doesn’t admit cut, we can use the same strategy as for CLV’: going through models. Again, these models themselves don’t matter at all for the main point; they are just a technical auxiliary to show that certain positions are not derivable in CLT’. The needed kind of model-theoretic strategy is a familiar one in theories of truth. It’s based on fixed points of a certain kind of function, and can be found (among other places) in Skolem (¹⁹⁶⁰, ¹⁹⁶³); Brady (¹⁹⁷¹); Martin and Woodruff (¹⁹⁷⁶); Kripke (¹⁹⁷⁵); Leitgeb (¹⁹⁹⁹).

Again, we work with strong Kleene models, now subject to much more complex restrictions on the assignments of values to atomics (and in particular atomics involving the predicate T). The fixed point strategy mentioned above is what ensures the existence of such models. I won’t here go through the details, but if you are familiar with the idea you will likely be able to see that there are going to be counterexamples available all over the place. In particular, if Γ∪Δ contains no Ts, ⟨⟩s, or M s, then [Γ⇒Δ] is derivable in CLT’ iff it is derivable in CL’ —that is, iff it is valid in first-order classical logic. This is perhaps a kind of conservativity, although here we have only a single language, so it is not the usual sort.

But many naive theories of truth can achieve that much: total classicality for the non-semantic language. ²³ What CLT’ achieves is more: total classicality for the full language. Remember, CL’ is in force for the entire language, and it already assures the derivability of every classically valid position. The added rules in CLT’ give us a naive truth theory, but they take nothing back. Negation functions just as it does, even when applied to sentences involving semantic vocabulary, or even the paradoxes themselves. So too does the rest of the UFO vocabulary. The conservativeness-like fact is important because it shows us that CLT’ has not fallen victim to the paradoxes. It should not be taken to exhaust the senses in which CLT’ is classically-minded, though. More important is what was emphasized above: every classically valid position, no matter what vocabulary it uses, is already declared out of bounds by CL’, and so by any of our stronger systems.

Validity and the bounds

Nowadays, paradoxes of validity are back in style. See, for example, Barrio, Rosenblatt, and Tajer (²⁰¹⁶); Beall and Murzi (²⁰¹³); Mates (¹⁹⁶⁵); Read (¹⁹⁷⁹, ²⁰⁰¹); Priest (²⁰¹⁰); Priest and Routley (¹⁹⁸²); Shapiro (²⁰¹¹); Zardini (²⁰¹³, ²⁰¹⁴). ²⁴ And that is reason enough to discuss them in Uncut: if the tools here can shed light on topics of interest to many, it’s worth seeing how. But there is another more pressing reason to discuss the paradoxes of validity here: the risk of revenge. I mean here the kind of revenge where key theoretical terms used to address the paradoxes turn out themselves to be paradox-prone, and to be paradox-prone in such a way that the theory they are part of can’t address the new paradoxes it engenders.

There is no risk of revenge of this sort arising here based on ‘true’. This is because there is no need, in presenting the theory I’ve given, ever to use the word ‘true’ at all. It’s an important piece of vocabulary in the object language, to be sure. After all, it’s a necessary ingredient in many of the paradoxes I’ve been talking about. But there’s no need to deploy ‘true’ in the theory of these paradoxes, or in our theory of meaning at all. As far as I can see, everything I want to say can be straightforwardly said in the ‘true’-free fragment of English.

Rather, if there is a risk of revenge, it is in the notion of a position’s being out of bounds. Familiar paradoxes of validity can easily be transposed into the language of the bounds. But I can’t seriously pretend that I could give a ‘bounds’-free version of what I’m doing! The bounds really are the central theoretical notion I’m drawing on. If this notion itself gives rise to paradoxes (as it may well), then those paradoxes too had better be resolvable along the lines I’ve already presented. It would be no good to say, for example, that all the paradoxes except for ‘bounds’ paradoxes are to be addressed by thinking carefully about the bounds, while ‘bounds’ paradoxes are to be addressed by appeal to a Tarskian hierarchy.

Here there is a bit of a puzzle, though. For ‘true’, there is a reasonably obvious naive theory of it. But what about ‘out of bounds’? This is a theoretical notion at its heart; while I intend it to be recognizable from our everyday conversational practice, I have quite deliberately refrained from even attempting a full theory of it. This doesn’t get me off the hook, though; it may be that we can say enough about how the notion behaves to see paradoxes in it.

Here’s a start. Let O be a predicate in our language that means ‘out of bounds’, and suppose we have a canonical name ⟨[Γ⇒Δ]⟩ for each position [Γ⇒Δ]. Then we might imagine rules like the following:

O⟨⟩D is named for the rule VD so named in Beall and Murzi (²⁰¹³) and also discussed under that name in Shapiro (²⁰¹³). On the present interpretation, O⟨⟩D says that if someone has adopted a position [Γ⇒Δ], then adding to that position an assertion that it is out of bounds results in a position that really is out of bounds. O⟨⟩R should be read as subject to a side condition: that Γ’ and Δ’ themselves consist entirely of claims about the bounds. Then it is best read contrapositively: it says that if it is in bounds to deny that [Γ⇒Δ] is out of bounds, then it is in bounds to go on and assert everything in Γ and deny everything in Δ. Because of the side condition, it doesn’t say that this applies to all background positions (which would be totally implausible); it applies only to background positions that themselves make no claims other than bounds claims. It’s an S4-ish kind of principle.

Both of these can be questioned; and they are in Uncut. But what I want to point out here is what the situation is if they do apply. So suppose they do. Then paradoxes arise involving the bounds. For example, consider the sentence that says of itself that asserting it is out of bounds. This is a sentence ν that is O⟨[ν⇒]⟩. This sentence poses a risk of paradox, via the following non-derivation:

It can be a bit tricky to see, but the only bad step in the above is the application of cut; the uses of the bounds rules are in fact correct.

I hope it’s clear how I’m going to respond to this paradox. It’s just like the other paradoxes we’ve looked at: the step of cut cannot be justified, and so this non-derivation doesn’t in fact go through. The empty position cannot be derived even if we take up constraints like O⟨⟩D and O⟨⟩R. This underivability claim, like the others, can be shown by a detour through models; details are in the book. Paradoxes involving the bounds can be handled in just the same way as more familiar paradoxes; the present approach doesn’t need to use any ad hoc machinery to address them. Revenge is thus avoided.