1. INTRODUCCIÓN
Desde hace varios años se ha insistido en que los estudiantes deberían adquirir la habilidad para modelar una amplia variedad de fenómenos (NCTM, 2013), lo cual ha impulsado la inclusión de la modelación matemática en los programas de estudio de diferentes niveles escolares. Como fruto de esta necesidad las instituciones han debido incluir modificaciones curriculares con la intención de que los estudiantes desarrollen habilidades para: (i) determinar y analizar las variables involucradas en una situación problemática, (ii) representar relaciones entre variables usando herramientas matemáticas, (iii) formular supuestos o hipótesis para simplificar la descripción matemática de fenómenos, (iv) interpretar los resultados y (v) tomar decisiones derivadas del análisis de un modelo (OCDE, 2013; NCTM, 2013). No obstante, para que estas modificaciones tengan éxito en el desarrollo del aprendizaje de los estudiantes, es preciso que el profesor domine algunos aspectos del conocimiento matemático y extra-matemático involucrados en el proceso de modelar, así como conocimientos didácticos y pedagógicos (Centiyaka, et al., 2016) para el diseño e implementación de actividades con modelación. Además, el docente debe diseñar y organizar ambientes de enseñanza donde se pone en juego su competencia para escuchar las ideas de los estudiantes, responder con sugerencias útiles, comprender enfoques inesperados, proponer representaciones útiles y establecer conexiones entre ideas o conceptos, ya sean matemáticos o de otros dominios (Doerr, 2007). Las diversas definiciones de lo que constituye la modelación, sus objetivos y procesos (Kaiser y Sriraman, 2006; OCDE, 2013; NCTM, 2013) también representan un reto para profesores y futuros profesores de matemáticas, ya que deben interpretar y dar sentido a estos conceptos para adaptarlos y llevarlos al aula.
Para responder al desafío curricular de incluir a la modelación en el aula de clases no basta la presentación de buenas tareas de enseñanza, como lo hacen algunos libros de texto, ya que el conocimiento y las concepciones del docente respecto de lo que significa modelar determinan la gestión de las actividades para el aprendizaje; por ejemplo, si considera que la resolución de problemas verbales es una actividad de modelado (Greer, 1997) o lo que entiende como problemas realistas (Kaiser, 2006). La variedad de interpretaciones sobre modelación que se puede encontrar en la literatura y la ambigüedad de su definición en algunos programas curriculares plantean la necesidad de conocer cuáles son las concepciones que sostienen profesores y futuros profesores de matemáticas, con la finalidad de comprender cómo se forman u organizan estas concepciones y tomar acciones desde la formación de profesores. El foco de atención en esta investigación se centra en el futuro profesor de matemáticas.
En la formación universitaria, el futuro profesor experimenta una transición entre el rol de estudiante y el rol de docente, proceso donde construye su identidad profesional a través de tensiones en su identificación con ambos roles y de sus concepciones cambiantes de lo que es o debería ser la enseñanza (Beauchamp y Thomas, 2009). En este contexto, considerando al futuro profesor como integrante de una comunidad que discute, reflexiona y organiza aspectos pertinentes para la enseñanza y aprendizaje de las matemáticas (profesor en práctica), exploramos las concepciones respecto de la modelación y cómo se evidencian a través del diseño de tareas para la enseñanza de las matemáticas. Lo cual, nos permitirá conjeturar sobre el impacto de las acciones pedagógicas del profesor en el aula (Frejd, 2012; Frejd y Bergsten, 2018) y proponer instancias con fundamentos empíricos para que el futuro profesor reflexione sobre sus concepciones y conocimiento necesario para la enseñanza de la modelación.
Con este objetivo indagamos en las concepciones que se hacen presentes en diferentes momentos de la formación profesional de los futuros profesores. Para ello nos preguntamos ¿Cuáles son las concepciones sobre modelación que sostienen los futuros profesores de matemáticas? Para dar respuesta a estas preguntas consideramos dos elementos relevantes: (1) el conocimiento matemático y didáctico de los docentes se construye paulatinamente en la formación académica y (2) las concepciones son moldeadas por las experiencias instruccionales (Thompson, 1992; Wenger, 1999). Observamos las concepciones de dos grupos de profesores de matemáticas en formación con distinto nivel de avance en sus estudios universitarios. Esto implica suponer que así como el conocimiento del futuro profesor se enriquece a partir de las experiencias vividas en su formación académica (Thompson, 1992), también su sistema de creencias- y por lo tanto sus concepciones- se modifican cuando se involucran, como miembros de comunidades de aprendizaje (Wenger, 1999), en actividades instruccionales (Kaiser, 2006). El análisis del diseño de tareas constituye un tema de investigación en educación matemática y, de acuerdo con Förster (2011), los aspectos que destacan en el diseño y análisis previo de una tarea reflejan características consideradas importantes por los profesores; por ejemplo, cálculos aritméticos u obtención de resultados con base en un modelo establecido. De forma que, analizamos las concepciones de los profesores en torno a la modelación a partir del tipo de tareas que proponen y del potencial que asignan a estas tareas como apoyo en la construcción de conocimiento y habilidades en los estudiantes (Frejd, 2015).
Para abordar la discusión propuesta, primero describimos las características de la modelación matemática y algunos acercamientos al estudio de las concepciones que nos servirán como fundamentos teóricos para desarrollar el análisis, posteriormente presentamos la metodología y el análisis de datos, para concluir con una discusión sobre los resultados encontrados.
2. ANTECEDENTES Y MARCO CONCEPTUAL
2.1. Modelación Matemática
La modelación matemática en educación ha sido explorada desde distintas perspectivas, tal es así que en la literatura se encuentra una amplia cantidad de trabajos en el tema, donde destacan diferentes acercamientos a su enseñanza y a las actividades que la constituyen, para dar un ejemplo aquí describimos brevemente algunos de ellos. Según Niss, Blum y Galbraith (2007) un modelo matemático es una tríada (D, M, f) en la que D es un dominio de interés extramatemático, M es un dominio matemático y f es un mapeo de D a M. El ciclo de modelado es un proceso recursivo en el que los objetos, relaciones, fenómenos, suposiciones y preguntas en D se identifican y seleccionan como relevantes y luego se mapean en objetos pertenecientes a M. Dentro de M, las imágenes de objetos, relaciones, etc. provenientes de D se operan y, con base en los resultados obtenidos en M se traducen de nuevo a D y se interpretan como conclusiones sobre ese dominio. También suelen usarse representaciones diagramáticas para ilustrar los procesos cognitivos y procedimentales asociados a la modelación (Doerr, Ärlebäck y Misfeldt, 2017). En otra perspectiva identificada por Kaiser y Sriraman (2006), el enfoque no está en el ciclo de modelación sino en el aprendizaje de conceptos matemáticos y el desarrollo de competencias con el fin de formar ciudadanos críticos y comprometidos con la sociedad.
Por otro lado, también se identifican dos perspectivas de la modelación, construcción de modelos y exploración de modelos (Doerr, 1995). La primera refiere al proceso en el que los estudiantes desarrollan herramientas conceptuales para comprender un fenómeno o una situación real, operar las representaciones matemáticas e interpretar los resultados en términos de la situación de referencia. En la otra perspectiva, el resolutor explora las consecuencias de operar o modificar modelos ya estadarizados de algún fenómeno dentro de los límites definidos por los mismos para derivar consecuencias y tomar decisiones. Adicionalmente, suele hacerse una distinción entre modelación y aplicación de las matemáticas, esta última es caracterizada por la aplicación o uso de modelos ya desarrollados para estudiar situaciones específicas (Blum y Niss, 1991). También, se hace una distinción en las actividades de modelación de acuerdo a sus objetivos, tipos y contexto de las tareas, competencias para los estudiantes, entre otros (Maaß, 2010). Por añadidura, Frejd y Bergsten (2018) advierten que la expresión modelado matemático o modelación matemática puede referir tanto al concepto de modelación como a la actividad de modelar.
En el contexto escolar, la organización para la evaluación internacional estandarizada PISA (OCDE, 2013) distingue, en un ciclo de modelación, los procesos matemáticos que un individuo pone en juego cuando resuelve problemas contextualizados: Formular (identificar oportunidades para usar las matemáticas), Emplear (aplicar conceptos y razonamiento matemático, manipular expresiones algebraicas y modelos) e Interpretar los resultados derivados de sus operaciones matemáticas. En la práctica, este es un enfoque que los profesores de matemáticas de secundaria siguen con frecuencia para cumplir con los requisitos de los estándares de evaluación nacionales e internacionales. Sin embargo, en diferentes países la interpretación de modelación en los currículos escolares tiene distintos enfoques (Borromeo, 2013). Particularmente, en Chile las bases curriculares señalan (MINEDUC, 2015):
[…] modelar es construir un modelo físico o abstracto que capture parte de las características de una realidad para poder estudiarla, modificarla y/o evaluarla; asimismo, ese modelo permite buscar soluciones, aplicarlas a otras realidades (objetos, fenómenos, situaciones, etc.), estimar, comparar impactos y representar relaciones. (p. 98)
Dada la variedad de puntos de vista desde donde se puede interpretar la modelación, en este trabajo no nos inclinamos por una postura en particular, sino más bien pretendemos observar aquellas perspectivas que se evidencian en las concepciones de los participantes.
2.2. Creencias y concepciones de los profesores
Al igual que en el caso de la modelación, las investigaciones en relación con las creencias y concepciones de profesores y estudiantes de matemáticas comprenden interpretaciones muy variadas. En cuanto a las creencias, existe una falta de consenso y precisión acerca de lo que constituyen, sobre su utilidad como predictores de la práctica docente y sobre los medios o herramientas apropiadas para obtener información acerca de este elusivo constructo (Skott, 2015). Respecto a las concepciones sucede lo mismo, mientras que algunos investigadores las asocian con la imagen de un concepto (Furinghetti y Pehkonen, 2002), otros investigadores las consideran como una noción más amplia o estructura mental que incluye creencias, significados, conceptos, reglas, imágenes mentales y preferencias (Philipp, 2007) o como sistemas de creencias, puntos de vista, preferencias e imágenes mentales (Thomson, 1984). Estas dos últimas definiciones son más cercanas entre sí.
Por otro lado, las creencias se estructuran mediante relaciones complejas que involucran aspectos que pueden no solo estar directamente relacionados con las matemáticas, pero que determinan la interacción del docente con los estudiantes, los contenidos temáticos y la forma en que aborda la enseñanza (Thompson, 1992). De manera que se observa una relación entre las creencias, el conocimiento y la gestión de los escenarios de instrucción, elementos que la noción de concepción acoge. Desde esta perspectiva, adoptamos la definición de Phillipp (2007), entendiendo a la modelación como una práctica matemática y como una estrategia de enseñanza. Donde las concepciones sobre la modelación dependen, en parte de las creencias con respecto a la naturaleza de las matemáticas (Ernest, 1989) y en parte de las preferencias sobre las aproximaciones a la construcción del conocimiento. Esta postura nos permite, evitar la discusión sobre si las creencias forman parte del conocimiento del individuo (Ponte, 1994), así de acuerdo con Frejd (2012) y Frejd y Bergsten (2018) hacer una distinción entre conocimientos, creencias, preferencias o imágenes mentales, no es objeto de discusión en este trabajo.
A pesar de la existencia de una amplia gama de trabajos relacionados con las creencias y concepciones de los profesores en formación sobre la enseñanza y aprendizaje de las matemáticas, poco se ha profundizado en la exploración en relación con la modelación (Frejd y Bergsten, 2018). En el caso de profesores con poca experiencia en actividades de modelación, Frejd (2012) encontró que sus concepciones se asociaban con el diseño de un modelo matemático basado en una situación con un contexto de la vida real, por ejemplo la simplificación para describir “algo” con matemáticas, y parecían no dar prioridad a la integración de la modelación en sus clases de matemáticas del día a día. Además, este autor encontró que las concepciones observadas en un 60% de los participantes podrían ser un obstáculo para la implementación de la modelación en el aula de clase. En una investigación posterior, Frejd y Bergsten (2018) determinaron cuatro aspectos clave relacionados al trabajo con modelación matemática y asociados a las concepciones de modeladores expertos (descripción, comprensión, abstracción y negociación) y con base en ellos propusieron algunos principios didácticos para el diseño de actividades de modelación. En investigaciones donde profesores y futuros profesores han tenido una formación específica para la enseñanza de la modelación, se han identificado cambios en sus concepciones relacionados con las características de las tareas de modelación y con las ventajas y desventajas de su implementación en el aula (Cetinkaya, et al., 2016).
2.3. Los modelos de enseñanza
Dos aspectos muy cercanos a las concepciones del profesor son los modelos de enseñanza y aprendizaje que posee (Ernest, 1989). Un modelo de enseñanza está constituido esencialmente por ideas que el profesor tiene acerca de la naturaleza y alcance de sus acciones en el aula, las cuales se manifiestan en las tendencias y orientaciones de enseñanza, dando prioridad a: lo investigativo, resolución de problemas, comprensión conceptual, el desarrollo de habilidades y combinaciones de estos. Por otra parte, un modelo de aprendizaje de las matemáticas, consiste de los puntos de vista que el profesor tiene sobre el aprendizaje de la disciplina, por ejemplo, qué comportamiento y actividades mentales involucra el aprendizaje. Los modelos de aprendizaje descansan básicamente en dos perspectivas: un punto de vista que apoya la construcción del conocimiento de manera significativa y un punto de vista que apoya el aprendizaje pasivo, como un receptor de conocimiento. Ernest (1989) señala que un profesor con una visión dinámica de las matemáticas tendrá inclinación por aceptar y fomentar diferentes enfoques de solución de problemas en sus estudiantes. Mientras que un profesor con una visión estática tenderá a favorecer un único camino para resolver las tareas. La concepción del profesor respecto a la relación de la matemática con otras áreas del conocimiento juega un papel relevante en las tareas que propone, ya que considerar a las matemáticas como integradas o aisladas de otras áreas del conocimiento (Ernest, 1989) se reflejará, por ejemplo, en los contextos en que se enmarcan las tareas: problemas con un contexto matemático, hipotético o real, problemas de palabras o actividades de modelación. De forma que, una manera de aproximarnos a la descripción de las concepciones de los futuros profesores es a través de la observación de la planificación de las tareas de enseñanza que proponen.
3. METOLOGÍA DE INVESTIGACIÓN
Indagar en las concepciones de los futuros profesores requiere de un análisis profundo, cercano y comprensivo del individuo, aspectos que en la investigación educativa se apoyan en la flexibilidad que ofrecen los métodos cualitativos de análisis (Denzin, 1978). Además, la complejidad que implica comprender las concepciones que los individuos sostienen y explicar las razones por las que actúan de cierta manera, nos conduce a situar la investigación en un estudio colectivo de casos (Stake, 1999).
3.1. Los participantes
Para dar respuesta a las preguntas de investigación analizamos las respuestas a una entrevista semiestructurada, a una serie de cuestionarios y el diseño de tareas desarrollado por profesores de matemáticas en formación quienes cursaban la carrera de pedagogía en matemáticas en una universidad chilena. Consideramos dos grupos de estudio un grupo (M) conformado por seis participantes (M1, …, M6) quienes habían cursado aproximadamente la mitad de las asignaturas correspondientes a la carrera y otro grupo (E) también formado por seis participantes (E7, …, E12) que se encontraban en el último semestre de sus estudios (8º semestre). Al momento de la investigación ambos grupos realizaban una práctica docente, con una duración de 2 y 6 meses, respectivamente. Nos interesamos en estos participantes por las concepciones que cada individuo puede tener, pero también por aquellas que pueden ser sostenidas colectivamente en grupos con distinto avance en sus estudios. Los participantes de M fueron seleccionados de un curso con 17 estudiantes y los de E de un curso con 15 integrantes. La selección se basó, por un lado, en la disponibilidad de los individuos para participar en la investigación. Y por otro lado, los participantes debían haber realizado o estar realizando alguna práctica profesional. Este aspecto es importante debido a que la práctica profesional constituye el primer acercamiento del futuro profesor al rol de profesor.
Durante los primeros dos años de su formación, los estudiantes de pedagogía cubren ocho asignaturas de matemáticas, cuatro asignaturas de pedagogía y una de didáctica de la matemática. Al concluir su formación habrán cursado 45 asignaturas, correspondientes a: matemáticas (14), didáctica (5) y pedagogía (8); además de haber realizado tres prácticas profesionales en el aula. La primera práctica puede realizarse a partir del segundo año de estudios. La formación académica es un factor que puede influir en las concepciones en ambos grupos de estudio, en el sentido que durante los primeros dos años los estudiantes cursan asignaturas de matemáticas, impartidas por matemáticos, donde la modelación es conceptualizada desde la perspectiva del matemático, tal es el caso del grupo M. En particular, los participantes del grupo E han cursado mayor cantidad de asignaturas de didáctica, pedagogía y realizado prácticas profesionales, en donde reflexionan sobre las potencialidades y limitaciones de distintas estrategias enseñanza. En las instancias de práctica profesional y en otros cursos, los participantes han diseñado diversas tareas orientadas principalmente a la enseñanza de distintos objetos matemáticos señalados en el currículo escolar. Estas tareas normalmente parten de una situación significativa para el estudiante, pero en realidad dependen del modelo de enseñanza del docente. Por otro lado, los programas de estudio de la pedagogía no explicitan la modelación como contenido a enseñar. Estas condiciones nos permiten capturar las concepciones que construyen los participantes en dos etapas distintas de su formación académica.
3.2. Las comunidades de práctica
Si bien es cierto que las concepciones son personales, y la mayoría de las investigaciones estudian los cambios que tienen lugar en ellas después de alguna intervención didáctica, observando al mismo grupo de individuos en diferentes momentos (Cetinkaya, et al., 2016), nosotros estudiamos las concepciones en dos grupos distintos de participantes, donde sin perder de vista la individualidad, consideramos un estudio colectivo de casos (Stake, 1999). Esta idea se apoya en las características que definen una comunidad de práctica: el dominio, la comunidad y la práctica (Wenger, 1999). Nos referimos a la comunidad de práctica en el sentido de que un grupo de futuros profesores participa de una red de conexiones con una identidad definida en torno a un mismo dominio de interés (didáctica, pedagogía y matemáticas). En la que los participantes comparten experiencias, reflexiones y aprenden unos de unos en un mismo entorno social. Asimismo, los miembros de un grupo construyen, en colaboración, un conjunto de recursos, tales como conocimiento sobre las matemáticas, experiencias y herramientas para la enseñanza. Y las interacciones dentro del grupo favorecen que los participantes expongan una postura respecto a la enseñanza y aprendizaje de las matemáticas, de manera que el individuo incorpora gradualmente, conscientemente o inconscientemente, a su sistema de creencias algunas de las ideas expresadas por los otros miembros de la comunidad o incluso desarrolla un criterio con relación a las opiniones divergentes.
3.3. Recogida y análisis de la información
La recogida de información se realizó a mediados del cuarto semestre para el grupo M y a mediados del octavo semestre para el grupo E por los autores, al mismo tiempo que uno de ellos guiaba la práctica de los dos grupos. Toda la información se recogió en forma digital de acuerdo a lo siguiente.
Atendiendo a la importancia de contar con diferentes criterios para la triangulación de datos (Denzin, 1978), diseñamos e implementamos distintos instrumentos que nos permitieran validar la información: (1) Una propuesta escrita de enseñanza basada en información sobre la metabolización del alcohol en el organismo, obtenida de una página de internet http://www.ojocientifico.com/4190/cuanto-tiempo-dura-el-alcohol-en-la-sangre (Anexo A), (2) un cuestionario y entrevista semiestructurada sobre las características de la tarea, (3) Cuestionarios tipo Likert sobre objetivos y habilidades relacionados con la modelación (anexos B, C y D), e (4) información institucional como los historiales académicos de los participantes y los programas de estudio. Los instrumentos de los puntos (2) y (3) fueron sometidos a validación por juicio de dos expertos, uno en modelación y un profesor-investigador encargado de la práctica profesional. Además, los diversos instrumentos de recogida de información contribuyen a la observación de distintos matices que dan forma a las concepciones, en el sentido de Denzin (1978), observando lo que la gente piensa o cree y lo que hace, constituyendo adicionalmente una herramienta para triangulación de datos.
La recogida de información se organizó en dos etapas. En la primera etapa los participantes trabajaron individualmente en el diseño de una situación de enseñanza, tomando como base la información expuesta en el anexo A. Para el diseño de la tarea, los participantes determinaron los objetivos de enseñanza, la modalidad, el tiempo de implementación, las trayectorias de solución esperadas, así como el nivel educativo donde sería implementada. De esta forma se logró que todos los participantes trabajaran alrededor de un mismo contexto, a la vez que se evidenció la toma de decisiones respecto a la demanda cognitiva, estrategias de solución y representaciones matemáticas en las tareas que diseñaron, develando así elementos del modelo de enseñanza sostenido por cada uno (Ernest, 1989). Adicionalmente respondieron en forma escrita a las preguntas: ¿Cómo modificarías el enunciado? ¿Qué preguntas podrías plantear? ¿Es posible encontrar por lo menos dos rutas de solución? ¿Qué habilidades esperarías que desarrollen los estudiantes al resolver la tarea? Los instrumentos utilizados en esta etapa nos permitieron identificar los aspectos más relevantes que son considerados en el diseño.
La segunda etapa consistió de una entrevista semiestructurada, en donde los participantes explicaron sus razones y motivaciones para diseñar la tarea en la forma en que lo hicieron, para ello nos guiamos en preguntas de carácter más general como: ¿Qué significa modelizar?, ¿Qué habilidades deberían dominar los estudiantes? y ¿Para qué deberían los alumnos aprender matemáticas? En esta etapa, los participantes respondieron a los cuestionarios B, C y D. A partir de estos cuestionarios exploramos las concepciones sobre la enseñanza de las matemáticas y la modelación que se asociaban a la propuesta didáctica que diseñaron.
3.4. Análisis de datos
Para el análisis de datos, consideramos inicialmente un sistema de categorías sobre las concepciones relacionadas con la modelación y las aplicaciones establecido a partir de la revisión de la literatura (Chapman, 2006; Frejd, 2012). Debido a la gran cantidad de información obtenida decidimos observar las concepciones con una mirada transversal, de manera que la atención se centró en: (1) el significado que otorgan al término modelación, (2) las concepciones sobre el papel de la modelación en el aula de clase y (3) las características de las tareas de modelación.
Las unidades de análisis se definieron con base en el objetivo de investigación y están constituidas por segmentos del texto de las producciones escritas y de las transcripciones de las entrevistas. Una vez que se determinaron las ideas más importantes asociadas a los elementos establecidos en los puntos 1, 2 y 3, señalados en el párrafo anterior, buscamos las relaciones entre ellas para formar un esquema de concepciones para cada uno de los grupos. Para la codificación se consideraron aquellos elementos que mostraran indicios de la pertenencia de las afirmaciones a determinada categoría, por ejemplo si consideran a la modelación como motivación para el aprendizaje de las matemáticas, como objetivo central del proceso de instrucción o como herramienta para ilustrar los contenidos matemáticos. En este contexto, también consideramos las estrategias de enseñanza a las que dan mayor relevancia: metacognitivas, técnicas de solución de problemas, y/o uso de problemas de la vida real para introducir el estudio de tópicos matemáticos (Chapman, 2006), de esta manera nuestras categorías se fueron concretando para describir las concepciones de acuerdo a la siguiente proyección (Figura 1).
4. RESULTADOS
En esta sección, presentamos inicialmente los resultados que nos llevaron a la identificación de cuatro temas asociados a la concepción sobre el significado de la modelación, posteriormente mostramos los temas asociados a las concepciones sobre las características de las tareas de modelación y sobre el papel de la modelación en el aula de clase evidenciados en el diseño de las tareas de enseñanza y en los cuestionarios.
4.1. El significado de la modelación
La codificación de las respuestas de los participantes nos llevó a la identificación de cuatro temas relacionados con el significado que otorgan a la modelación. En particular, en las respuestas a la pregunta ¿qué significa modelar?, presentada en la entrevista semiestructurada, identificamos las concepciones de los profesores en formación con respecto al modelado, donde destacan cuatro aspectos principales: modelación como un medio de representación (Representación); modelación como aquellas actividades que pueden ser relacionadas con la solución de un problema en un contexto particular (Contexto); modelación como una actividad asociada a un objetivo (Objetivo), y la modelación asociada a las fases o procesos que la constituyen (Proceso). Estos se presentan a continuación.
Modelos matemáticos como una representación semiótica y modelación como una actividad representacional. En este tema se agrupan aquellas respuestas en donde los participantes reconocen a la modelación como una acción que conduce al planteo de un modelo matemático dado por una representación matemática, también destaca la identificación de la relación de un modelo con una representación matemática. La mayoría de los integrantes de M relaciona un modelo con una representación gráfica, mientras que los participantes de E lo relacionan con una representación algebraica, haciendo referencia a la idea de función. Ambos grupos señalan que un modelo involucra una relación entre variables. Los integrantes del grupo M lo hacen de manera implícita y los del grupo E lo explicitan con mayor frecuencia. Además, los integrantes del grupo E reconocen a la modelación como la acción de representar con elementos matemáticos. Mostramos a continuación dos respuestas representativas.
M1 - [Modelar consiste en] representar elementos matemáticos que estén relacionados mediante un dibujo, o sea un gráfico que muestra el comportamiento de la relación de los elementos matemáticos.
E8 - [Modelar] es utilizar el lenguaje algebraico para representar una situación y/o fenómeno de la vida cotidiana o diversos contextos con el fin de dar respuesta a interrogantes que puedan surgir. Se debe establecer con variables que están en juego en el fenómeno para formar una función.
Modelación como un proceso esta concepción se observó en ambos grupos, asociado al tránsito entre la Situación que se desea explorar y un Modelo Matemático. Los participantes del grupo M consideraron que un modelo está compuesto por un conjunto de datos, que son manipulados u operados para obtener información sobre una situación. Los participantes del grupo E consideraron que un modelo esta constituido por una expresión algebraica y el modelado consiste en manipular una ecuación o función con el objetivo de resolver un problema de la vida real o una situación puramente matemática.
M5 - Modelar es un proceso en el cual se extrae toda la información correspondiente a partir del enunciado para luego desarrollar el problema según las necesidades o condiciones…
E7 - [Modelar] Es plantear, mediante el uso de lenguaje algebraico una situación en un contexto matemático, o bien, un contexto de la vida diaria; para resolver una problemática que se pueda desprender de la situación.
Los participantes de ambos grupos hacen referencia a un proceso reconociendo elementos asociados al mundo de la realidad y al mundo de las matemáticas, pero no mencionan las fases que constituyen el ciclo de modelación (Doerr, Ärlebäck y Misfeldt, 2017). Por otro lado, los participantes de E refieren a un ciclo que podría tener el carácter Contexto-Modelo-Contexto, mientras que la mayoría de los participantes en M refieren al tránsito Contexto-Modelo, resultados que concuerdan con las investigaciones de Crouch y Haines (2007) quienes al observar la actividad matemática en modeladores expertos y novatos, encontraron que los novatos consideraban al proceso de modelación como lineal, no así los expertos. Este hecho también puede estar relacionado con la utilidad u objetivo que los individuos asignan a la modelación y las conexiones que establecen entre ésta y las matemáticas, como se discute líneas adelante.
Objetivo de modelar. En este tema se agrupan aquellas respuestas que hacen referencia a los objetivos de las actividades de modelación, por ejemplo comprender, describir y predecir. La mayoría de los participantes del grupo E muestra una tendencia pragmática hacia el modelado como un medio para interpretar, conocer, comprender, explicar, responder y tomar decisiones.
E10 - Modelizar para mi significa que se busca en una situación un modelo asociado, para conocer o comprender mejor dicha situación. Por ejemplo en una situación de crecimiento poblacional, modelizar sería buscar un modelo matemático asociado, un modelo socio-cultural asociado, o un modelo étnico asociado, etc. respecto de la situación, para conocer más sobre ese crecimiento y comprenderlo mejor.
E11 - La modelización se relaciona con el objetivo de explicar cómo funciona un sistema [natural o social], considerando los factores relevantes, las variables y el contexto […]
Los integrantes del grupo M al parecer consideran que modelar es un proceso cuya finalidad es representar algunas características del fenómeno, como se mostró en líneas anteriores (M1, M5), lo cual podría denotar una visión esquemática de la modelación (Kaiser, 2006), asociada a una perspectiva instrumentalista sobre la naturaleza de las matemáticas (Ernest, 1989). Los participantes del grupo E evidencian preferencias por el trabajo con representaciones algebraicas cuya finalidad es ayudar a la gente a comprender una situación, mostrando con ello una inclinación hacia lo formalista y el modelo es considerado como una herramienta para responder cuestionamientos. Las diferencias en las concepciones entre ambos grupos puede originarse en las creencias que tienen sobre la aplicación de las matemáticas o con su visión de la modelación como un proceso útil para resolver problemas (Ernest, 1989).
El contexto de las tareas de modelación. Los participantes, en general, no mostraron preferencia por algún tipo de contexto (hipotético, real, social, matemático). Los miembros del grupo M, en su mayoría, hacen referencia a una “situación” sin explicitar el tipo de contexto que podría tener. Quienes refieren a un contexto (la mayoría miembros de E) sitúan una problemática en entornos sociales, culturales, cotidianos y de la naturaleza. Para los participantes el contexto que da lugar a un proceso de modelación puede ser asociado con todo aquello que se encuentre fuera del mundo de las matemáticas.
Los resultados anteriores se resumen en la siguiente tabla (Tabla 1).
Tabla 1. Temas asociados al significado de modelación identificados en los grupos M y E
| Temas | Grupo M | Grupo E |
|---|---|---|
| Representación (como modelo y como actividad) | Modelos matemáticos relacionados con una representación gráfica | Modelos matemáticos relacionados con lenguaje algebraico, funciones y ecuaciones |
| Modelación como un proceso | Solo una parte del ciclo de modelación realidad- modelo matemático es considerada | Se considera el ciclo de modelación implícitamente como la relación realidad-modelo matemático- realidad |
| Objetivo de modelar | Un modelo matemático es considerado como un medio de representación útil y como medio para aplicar las matemáticas | Asignan un carácter pragmático al modelo, como una herramienta que les permite interpretar, explicar, obtener información y tomar decisiones respecto a la situación que originó el modelo |
| Contexto de las tareas de modelación | La realidad no es explícitamente señalada en los procesos de modelación | Se destaca la realidad en el proceso de modelación |
4.2. Las características de las tareas de modelación
Una manera de anticipar las características de la práctica de enseñanza es a través del análisis de los aspectos que los futuros profesores consideran relevantes en el diseño de las tareas (Simon y Tzur, 2004). A continuación se discuten los resultados de analizar el reporte escrito y la entrevista semiestructurada que evidencian la planificación de una tarea de enseñanza y la actividad esperada de los estudiantes. Analizamos la formulación de la tarea, las preguntas planteadas y los caminos hipotéticos de solución asociados a la tarea.
Antes de pasar al análisis de las tareas, se comentan algunos puntos clave para abordar el estudio de la situación que sirvió de base para el diseño de la tarea (Anexo A). Se debe conocer, la cantidad de alcohol presente en distintas bebidas, las proporciones entre volumen de bebida y alcohol consumido, las unidades de medición de la alcoholemia (gramos del alcohol/litro de sangre). Además, si la intención es la construcción o exploración de modelos matemáticos para describir o predecir el comportamiento del fenómeno, debería conocerse que la concentración de alcohol puede aproximarse mediante una función lineal considerando los gramos de alcohol consumidos y que la concentración de alcohol en un individuo posterior al consumo puede calcularse mediante C=d/m.r (C- la concentración máxima en el cuerpo (g/l), d- la dosis de alcohol (g), m- peso del individuo (kg), r- constante de distribución del alcohol en el cuerpo (l/kg)). Para abordar el diseño de la tarea los participantes fueron incentivados a investigar esta información. Describimos a continuación las características de las tareas diseñadas.
Formulación de la tarea y actividad intencionada. Los integrantes del grupo M, en general, no propusieron modificaciones relevantes al texto que se les presentó, redujeron la información presentada e identificaron los datos importantes. Mientras que los miembros del grupo E filtraron y organizaron la información en el texto. La mayoría de los participantes en E introdujo el uso de variables y propuso un modelo matemático (por ejemplo E11 líneas adelante) para describir la situación de referencia. A continuación se muestran dos ejemplos del texto presentado por E1 y E2.
E1: A través de una prueba de alcohol, se determinó el tiempo que tarda el organismo en eliminar el alcohol ingerido. El alcohol se mide en unidades; una unidad de alcohol equivale a 10 ml del 100% del líquido (256 ml de cerveza). Si una persona ingiere 500 ml de cerveza, el cuerpo necesita 2 horas para eliminar todo el alcohol de la sangre. ¿Cuántas horas se necesitan para eliminar 1200 cc de cerveza?
E2: Se sabe que un hígado sano es capaz de metabolizar una unidad de alcohol (10 ml de alcohol 100%) en una hora. ¿Cuánto tiempo se tarda en metabolizar 500 ml. de cerveza, si tiene una unidad de alcohol por cada 236ml?
Por otro lado, dos de los seis participantes (M2, M3) de M propusieron explícitamente la construcción de un modelo matemático para representar la situación, pero no dieron continuidad al proceso de solución que conduciría a la construcción del modelo. Por ejemplo M2 planteó la siguiente pregunta:
M2: ¿Puedes hacer una expresión la cual represente las unidades de alcohol, dados los mililitros del tipo de alcohol y las horas aproximadas que tarda el cuerpo en metabolizar dicha cantidad de alcohol?
M3: […]“Ayuda a Paolita a saber cuánto duró el alcohol en su sangre”, con el fin de plantearles una historia en la cual Paolita bebió alcohol (llamémosle A) y entregarles datos de las cantidades de A, del metabolismo y otros datos para que el estudiante pueda inferir una función […] que permita modelizar el proceso de evolución del alcohol A en la sangre de Paolita.
El resto del grupo (M) se enfocó en favorecer el desarrollo de cálculos aritméticos para inferir resultados sobre el tiempo o la cantidad de alcohol. En la mayoría de las preguntas planteadas por ambos grupos, destaca la exploración de relaciones de proporcionalidad, por ejemplo “¿cuántas unidades de alcohol tienen 500 ml. de cerveza?”. También se observa que las preguntas tienen una intencionalidad predictiva.
En las preguntas que los integrantes de E propusieron se observa una preferencia hacia el estudio de funciones lineales y la actividad se dirige a la inferencia de resultados con base en el estudio de un modelo explícito, algebraico o gráfico (E11). Mientras que los integrantes de M consideraron un modelo matemático, pero en forma implícita, es decir la presentación de la información en la tarea obedece a un comportamiento lineal, sin mostrar la expresión matemática correspondiente (M6). Los siguientes fragmentos del texto del informe escrito ilustran lo anterior.
Trayectorias de solución previstas. Aunque se pidió a los participantes analizar al menos dos caminos de solución para la tarea que plantearon, sólo dos miembros de cada grupo resolvieron la tarea completamente. Los integrantes del grupo M (M1 y M2) centraron la atención en las relaciones de proporcionalidad, mientras que los del grupo E (E7 y E11) propusieron sustituir valores en una expresión algebraica. Esto se puede observar en los siguientes ejemplos donde M2 y E11 describen el proceso de solución.
M2: ¿Cuántas unidades de alcohol tienen 250 ml de vino? Para responder a la pregunta 1, se puede hacer una proporción de los 10 ml de alcohol puro que el cuerpo tarda aproximadamente 1hr en metabolizar por lo tanto
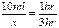 y así luego de resolver concluir que 250 ml de vino tienen aproximadamente 3 unidades de alcohol, lo que equivale a unos 30 ml de alcohol puro.
y así luego de resolver concluir que 250 ml de vino tienen aproximadamente 3 unidades de alcohol, lo que equivale a unos 30 ml de alcohol puro. E11: Así, se consume x cantidad de alcohol un 1% es eliminado por evaporación, un 10% por los riñones y el porcentaje que queda va al hígado lo que corresponde a:
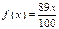 . Si se ingirió 250ml de vino ¿cuánto queda en el hígado? x= 250 ml del vino,
. Si se ingirió 250ml de vino ¿cuánto queda en el hígado? x= 250 ml del vino, 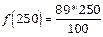 . Si se consumen 250 ml de vino, en el hígado quedan 222.5 ml.
. Si se consumen 250 ml de vino, en el hígado quedan 222.5 ml.
Demanda cognitiva. Observamos la demanda cognitiva de las tareas a partir de la actividad que los participantes proponen para los estudiantes. Sin embargo, lejos de proponer tareas con múltiples estrategias de solución, distintas representaciones y, que favorecieran la explicación y justificación de los procesos desarrollados (Henningsen y Stein, 1997), encontramos que dichas tareas fomentan el uso de procedimientos algorítmicos, tales como el cálculo de proporciones y la sustitución de un valor en una expresión matemática dada, actividades que son más cercanas a la resolución de un ejercicio que a un problema de modelación (Greer, 1997). Esto se evidencia en las respuestas de M4 y E8 quienes señalan de manera muy general como debería abordarse la tarea:
M4: Hay que ver como varía la cantidad de alcohol en la sangre durante el tiempo y para ver si es directamente proporcional e inversamente proporcional se puede graficar y ver, si aumenta una variable y aumenta la otra es directamente proporcional, es inversamente proporcional si aumenta una y disminuye la otra.
E8: Podría responderse con proporciones, planteando una ecuación, una función (método gráfico) o extrapolación lineal
Del análisis anterior, se identifican cuatro temas asociados a las concepciones de los futuros profesores y relacionados con el diseño de tareas. En primer lugar, la manera en que replantean la situación, evidencia que identificar información relevante es un factor relevante para los participantes de ambos grupos. Sin embargo, también muestra una debilidad en el conocimiento extramatemático y pedagógico para el diseño de actividades de aprendizaje basadas en modelación, puesto que no se reconocen los procesos de interpretación y reinterpretación de la realidad (Doerr, Ärlebäck y Misfeldt, 2017), tampoco se observa alguna intencionalidad para el desarrollo de competencias de modelación (Maaß, 2010). Si bien, los participantes reconocen que la realización de inferencias y, la construcción y exploración de modelos matemáticos deberían estar presentes, en la tarea diseñada se refleja mas bien un énfasis en el trabajo aritmético. Por tanto, nos encontramos ante un dilema entre lo que los participantes expresan que debería hacerse, en contraste con lo que se evidencia en la tarea que diseñan. La manera en que reescriben la tarea, el tipo de actividades y las soluciones que prevén dan cuenta de concepciones más cercanas a la resolución de problemas de palabras. En la siguiente tabla (Tabla 2) se resumen los temas asociados a la concepción sobre las características de las tareas de modelación.
Tabla 2. Temas relacionados a la concepción sobre las características de la tarea evidenciadas en el diseño.
| Temas | Grupo M | Grupo E |
|---|---|---|
| Identificación de información relevante | No reformulan el enunciado, ofrecen indicaciones generales de como se podría modificar la situación. | Algunas modificaciones al enunciado son propuestas, dirigidas a la simplificación de los datos involucrados |
| Actividad de aprendizaje (preguntas a responder) | En las preguntas no se hace referencia a la construcción de un modelo. El carácter de las preguntas es estático (sólo se busca obtener la respuesta). Vinculan sus preguntas con diferentes niveles educativos | Sólo un participante propone construir un modelo matemático. Involucran el rol del tiempo en sus preguntas. |
| Carácter del modelo matemático | Modelo matemático implícito relacionado con la proporcionalidad, de carácter aritmético. No proponen realizar inferencias con base en la información obtenida del modelo. No se considera la exploración de modelos matemáticos. | El modelo involucra una función o ecuación. Se propone que los estudiantes realicen algunas inferencias. Se propone la exploración de modelos matemáticos ya establecidos. |
| Naturaleza de la modelación matemática | No se aborda la toma de decisiones con base en la exploración o manipulación de los modelos matemáticos. | Se sugiere realizar inferencias sobre el fenómeno y tomar decisiones con base en el modelo visto como una función. |
Observamos, en ambos grupos, preferencias por favorecer actividades como la identificación de variables y relaciones para representar matemáticamente una situación, obviando aspectos como la simplificación e idealización y la comprensión de las relaciones entre el lenguaje del contexto y el simbolismo matemático. Al comparar las preguntas y los procesos de solución que los participantes muestran, se observa que el grupo M se enfoca en el desarrollo de cálculos aritméticos y el grupo E en las manipulaciones simbólicas. Los participantes de ambos grupos raramente refieren a actividades que conduzcan a la generalización o reflexión sobre argumentos matemáticos, soluciones y conclusiones, menos aún consideran la interpretación de los resultados en términos del contexto. Los argumentos del grupo E, al señalar las habilidades pertinentes a desarrollar, son más descriptivos, hecho que nos permite inferir que consideran la construcción y/o aplicación de un modelo matemático, pero esto no se hace evidente en las tareas que proponen. También emerge la idea relacionada con la enseñanza de las matemáticas para el desarrollo de habilidades sociales y para enfrentarse a situaciones de la realidad e interdisciplinares. Los miembros del grupo E plantean el desarrollo de habilidades en un formato acorde con los programas de estudio, donde es clara la influencia que ha tenido su paso por la universidad.
4.3. El papel de la modelación en el aula
Complementamos el análisis del reporte escrito con las respuestas al cuestionario del anexo B donde identificamos las habilidades que los participantes esperan que sus futuros estudiantes desarrollen. Para mejor visualizar la distribución de preferencias los datos se categorizaron en tres niveles: menor acuerdo, acuerdo medio y mayor acuerdo. Los miembros del grupo M se muestran más de acuerdo que los miembros del grupo E en que la tarea favorece el desarrollo de habilidades para interpretar y emplear las matemáticas (items b, c), las diferencias en el porcentaje de acuerdo entre los participantes están dadas por 33.3% y 50%, para cada item. La dificultad encontrada para construir un modelo por parte de los participantes (66.7%) del grupo M, es reflejada al considerar que el contenido matemático es relativamente complejo (item f), razón por la cual podrían considerar que es importante darle mayor orientación al estudiante durante el proceso de solución (item e, 66.7%). Aproximadamente, el 66.7% de los miembros del grupo E, considera que el contenido matemático implicado en la tarea es poco complejo. De aquí podemos interpretar que las concepciones de los futuros profesores respecto a la enseñanza de la modelación podrían forjarse a partir de consideraciones respecto a la complejidad o dificultad que ellos mismos encuentran en la resolución de tareas o situaciones problemáticas.
Los datos obtenidos del instrumento C (anexo C) se presentan categorizados de acuerdo a tres niveles: menor importancia, importancia media y mayor importancia. En una perspectiva más general, al indagar sobre el rol que deberían tener las tareas de modelación en el aula de clases, encontramos que aproximadamente el 83.3% de los participantes del grupo M otorgan mayor importancia a que los estudiantes aprendan a establecer relaciones entre el mundo real y las matemáticas (item 5). El desarrollo de habilidades cognitivas (item 6) es apoyado en mayor importancia por el 66.7% y el aprendizaje de las matemáticas en la forma en que fueron desarrolladas es apoyado por el 16.7% de los participantes. Mientras que el 83.3% de los miembros del grupo E, otorgan mayor preferencia al desarrollo de habilidades cognitivas (item 6), las habilidades de carácter pragmático como lo es resolver problemas de la vida real (item 1), son apoyadas en mayor importancia por el 66.7 % y menor preferencia es otorgada al aprendizaje de las matemáticas y las ciencias en forma conjunta (item 2, 16.7%). En cuanto al aprendizaje del proceso para resolver problemas que se presentan con un contexto, el 50% de ambos grupos le otorgan similar importancia. Los aspectos socio-críticos e histórico-epistemológicos tienen menor preferencia (item 3 y 4) para el 83.3% y 66.7% de los participantes. De lo anterior, parece ser que los participantes del grupo M mantienen una visión más global sobre el rol de la modelación como herramienta para entender el mundo y resolver problemas de la vida real y los miembros del grupo E se enfocan más en el desarrollo de habilidades cognitivas. Estas diferencias podrían deberse a que los participantes del grupo E se encuentran en la fase final de su proceso de formación y tienden a reflexionar con mayor profundidad sobre el tipo de actividades que potencian un aprendizaje significativo.
Las percepciones sobre la utilidad de la modelación (anexo D) en el aula de clase son muy parecidas en ambos grupos (M y E). Ambos grupos consideran en primer lugar a la modelación como medio para el desarrollo de conceptos matemáticos, en segundo lugar como estrategia de enseñanza, en tercer lugar como motivación y finalmente como parte del currículo. Estos aspectos se ven poco reflejados en las propuestas de enseñanza elaboradas en el grupo M, debido a que se centran más en la observación de las relaciones presentes sin referir a los conceptos matemáticos implicados, no así los miembros del grupo E quienes hacen referencia explícita a conceptos como función, ecuación, solución de una ecuación y extrapolación.
5. DISCUSIÓN Y CONCLUSIONES
La literatura muestra que la mayoría de las investigaciones sobre las concepciones relacionadas con la modelación han sido desarrolladas con profesores que han tenido participación en algún curso de modelación (Cetinkaya, et al., 2016), además han sido realizadas en países con una cultura sobre la enseñanza y aprendizaje de la modelación matemática (Kaiser, 2006) distinta a la realidad de nuestros participantes. En esta investigación reportamos los resultados obtenidos en un programa de formación docente en donde el modelado está en proceso de inclusión en los programas de estudio. Por lo tanto, la falta de experiencia al abordar problemas de modelación se refleja en su forma de pensar la enseñanza de la modelación.
Metodológicamente, la dificultad que introduce el uso de cuestionarios y encuestas, en el sentido de que al responder a una pregunta, el participante no ha pensado previamente en ello (Philipp, 2007), se abordó proporcionando a los participantes un contexto para la acción a través del diseño de una tarea. Así, los resultados de está investigación se sustentan en el análisis complementario de los datos obtenidos, principalmente a través del diseño escrito de una tarea de modelación y las respuestas a varios cuestionarios. A partir de la entrevista encontramos que las concepciones sobre la modelación en la enseñanza de las matemáticas se relacionan con cuatro categorías o temas principales: representación, proceso, objetivo y un contexto. Mientras que, a través del diseño de tareas de modelación evidenciamos transversalmente, en la formulación de la tarea y actividad intencionada para los estudiantes, en las trayectorias de solución previstas y en la demanda cognitiva, aspectos asociados a las concepciones sobre las tareas de modelación que se distinguen de acuerdo a: identificación de información relevante, actividad de aprendizaje o acciones para el aprendizaje, carácter del modelo matemático y naturaleza de la modelación matemática. Mediante las respuestas a los cuestionarios identificamos elementos asociados a la percepción sobre las habilidades que se potencian con la modelación y el rol de la modelación en el aula de clase, los cuales complementan el panorama sobre el estudio de las concepciones que se aborda en este artículo.
Se observaron diferencias en la concepción sobre la modelación entre ambos grupos. En el grupo M, se consideró al modelo matemático como un elemento implícito de la actividad matemática y la actividad de modelado se orientó hacia la realización de cálculos aritméticos. En el grupo E, se consideró al modelo como medio para obtener resultados, con un carácter más pragmático. Una de las principales características encontradas en las concepciones se asocia a la consideración de un modelo implícito (dado por cálculos aritméticos) en el grupo M, hasta considerar un modelo matemático que representa una situación y finalmente a considerar la construcción de un modelo matemático basado en el estudio de fenómenos, aun en desarrollo en el grupo M. Esta última característica se ha evidenciado más frecuentemente en docentes con varios años de experiencia (Frejd, 2012).
En la entrevista los participantes de ambos grupos, asociaron la modelación con una visión de carácter instrumentalista (Ernest, 1989), considerando a los modelos como herramientas para obtener información respecto a una situación, pero al asumir el papel de profesor durante el diseño de la tarea de enseñanza le asignaron el rol de una actividad facilitadora para el desarrollo de habilidades cognitivas (Chapman, 2006), posturas que no se contradicen. Aunque si se puede observar una divergencia entre las ideas que expresan y las tareas que proponen. En este sentido, los participantes que se encuentran al final de sus estudios tienen más experiencia en la práctica docente y sus concepciones también han sido influenciadas por sus interacciones dentro de la comunidad profesional, por lo que muestran mayor claridad en el diseño de la tarea con objetivos de aprendizaje mejor definidos.
Si bien los participantes de ambos grupos reconocen a la modelación como un proceso que relaciona la realidad y el mundo de las matemáticas, no se identificó el proceso como un ciclo integrado por distintas fases (Doerr, Ärlebäck y Misfeldt, 2017), por lo que en el diseño de la tarea toman en cuenta principalmente las relaciones entre el contexto y las representaciones matemáticas. Las tareas de modelado para los participantes constituyen medios para el desarrollo de conceptos y una estrategia de enseñanza, donde el producto final son las respuestas a preguntas planteadas sin dar importancia a la generalización o uso de modelos matemáticos para explicar una situación o tomar decisiones. Beswick (2012) explica que este comportamiento puede estar sustentado en las diferencias entre las matemáticas que desarrollan los matemáticos y las matemáticas del aula de clase, indicando que en el aula los estudiantes trabajan con problemas seleccionados por el profesor para ser resueltos en un tiempo determinado, mientras que los matemáticos tienen autonomía sobre los problemas que resuelven y trabajan en ellos durante tiempos prolongados, similar al trabajo que desarrollan los modeladores expertos. Estos resultados nos conducen a insistir, en la necesidad de incluir y discutir el rol de la modelación en el aprendizaje de las matemáticas en los cursos de formación de profesores, donde es importante que los individuos se involucren activamente y adquieran experiencia en el diseño y solución de actividades de modelación (Kaiser, 2006). Además, estudiar la evolución de las concepciones sobre modelación y la enseñanza de las matemáticas en los futuros profesores, y las acciones que tienen impacto en ellas es un tema que queda abierto para futuras investigaciones.
Finalmente, destacamos que el estudio de las concepciones relacionadas con la modelación, requiere de un marco conceptual y metodológico estructurado con herramientas que permitan capturar los distintos matices que dan forma a las concepciones, puesto que el solo hecho de elegir la pregunta o la tarea constituye la toma de una o diversas posturas filosóficas, didácticas y pedagógicas, frecuentemente inconscientes para el individuo y que abarcan más allá de conocer la definición o el proceso de modelación. Aspectos que son construidos por la participación de los individuos en la comunidad de aprendizaje. Respecto de la complementariedad de instrumentos para la recogida de información queda pendiente la implementación de instrumentos que permitan profundizar en las concepciones que subyacen a las fases de modelación.