INTRODUCCIÓN
La Geometría Analítica es un área de las Matemáticas que proporciona la resolución de problemas geométricos por métodos algebraicos. El estudio de esta área tiene gran relevancia en la resolución de diferentes situaciones, con aplicaciones en Matemáticas, Física, Arquitectura e Ingeniería, sirviendo de base para áreas más modernas, como Geometría Discreta, Geometría Computacional, Geometría Diferencial y Geometría Algebraica. Sin embargo, la comprensión del tema requiere la asimilación de una abstracción matemática por parte del estudiante, lo cual muchas veces es visto de manera negativa, generando resistencia y siendo un obstáculo en su aprendizaje.
Existen dificultades que permean la Geometría Analítica asociadas al área de Cálculo Diferencial e Integral y una de ellas es el aprendizaje de superficies cuádricas (Silva, 2018). En la Educación Superior, entre los tipos de superficies estudiadas se encuentran las superficies cuádricas que, algebraicamente, tienen como registro simbólico una ecuación cuadrática en tres variables.
Al buscar materiales con diferentes enfoques de las cuádricas, nos encontramos ante un número limitado de obras. Muchos trabajos traen el estudio de la Geometría Analítica con el uso de tecnologías, pero un número muy escaso trae un enfoque específico al estudio de las cuádricas. En la tesis de Silva (2018), el autor atribuye la ausencia o superficialidad en el abordaje de este tema a su complejidad, debido al tiempo didáctico y a las dificultades expresadas por los docentes en la transposición didáctica de este tema de manera efectiva.
Según Suleiman (2016), las dificultades de los docentes en determinados temas de Matemática, en ocasiones por razones de tiempo para la planificación y posterior estudio, hace que no puedan conectar diferentes temas dentro de la disciplina, su relación con la realidad y su aplicabilidad, provocando la aparición de obstáculos didácticos, lo que impacta en el aprendizaje de sus alumnos. En este sentido, Alves (2012) trae un hallazgo sobre el bajo rendimiento, la frágil evolución del aprendizaje y las dificultades inherentes a la transición del contexto escolar al ambiente académico, en lo que se refiere al estudio del Cálculo Diferencial asociado a la Geometría Analítica y su consecuente evolución para las cuádricas.
Por lo tanto, la pregunta es: ¿cómo se podría trabajar el contenido de las cuádricas en el aula de grado de Matemáticas, en un enfoque visual e interactivo, con una mayor exploración de sus diferentes formatos y ecuaciones a través de recursos tecnológicos?
Para ello, el objetivo de este trabajo es presentar una propuesta didáctica para abordar la exploración de los tipos de cuádricas a partir de sus ecuaciones canónicas, enfatizando su transposición didáctica con el aporte de GeoGebra 3D, buscando ayudar a los estudiantes en su comprensión a partir de la visualización geométrica.
La metodología adoptada para este trabajo es la Ingeniería Didáctica (ED), ya que la ED es un método que trae “la opción por una perspectiva sistemática de preparación, concepción, planificación, modelado y, eventualmente, la ejecución y/o replicación de secuencias didácticas estructuradas” (Alves & Dias, 2019, p. 2).
En este caso, por tratarse de una investigación en curso, presentamos en este trabajo únicamente las dos primeras fases de la Ingeniería Didáctica, que son los análisis preliminares, como una forma de hacer un recorrido epistemológico y didáctico en la enseñanza de las cuádricas, y el análisis a priori, que trae la concepción y descripción de una situación didáctica propuesta para trabajar el tema con el uso del software GeoGebra en su ventana 3D. Según Breda et al. (2013), con funcionalidades 3D, GeoGebra hace más accesible la representación de elementos en el espacio, ayudando a comprenderlos a través de la visualización.
Con base en lo anterior, en las siguientes secciones presentamos el marco teórico de este trabajo basado en los presupuestos de la Ingeniería Didáctica, trayendo los análisis preliminares, con un aporte teórico, y el análisis a priori, que esboza la propuesta didáctica para el abordaje de este tema, seguido de las consideraciones de los autores.
INGENERÍA DIDÁCTICA
La Ingeniería Didáctica (ID) es una metodología de investigación derivada de los estudios relacionados con la Didáctica de las Matemáticas, de origen francés. Esta metodología se utiliza en investigaciones que estudian los procesos de enseñanza y aprendizaje de un contenido y, en particular, la “elaboración de génesis artificial para un concepto dado” (Almouloud & Coutinho, 2008, p. 66).
Según Artigue (1996), la ID se caracteriza como un esquema experimental basado en logros didácticos en el aula, es decir, en el diseño, realización, observación y análisis de secuencias didácticas. En otro trabajo, Artigue (1995, p. 37) reitera que “la metodología de la Ingeniería Didáctica se caracteriza también, frente a otro tipo de investigaciones basadas en la experimentación en el aula, por el registro en que se ubica y por las formas de validación a la que está asociado”.
Según Leivas y Gobbi (2014, p. 184) “esta metodología puede entenderse tanto como una metodología específica de investigación como una secuencia de clases o actividades concebidas y organizadas de manera coherente”. Siguiendo sistemáticamente esta metodología en su planificación y ejecución, debemos guiarnos a través de las fases: i) Análisis preliminares, ii) Concepción y análisis a priori de situaciones didácticas, iii) Experimentación y iv) Análisis a posteriori y validación. En resumen, cada una de estas fases puede describirse como:
i) Análisis preliminares: Se compone del estudio epistemológico del objeto de investigación, a través de una búsqueda bibliográfica en cuanto al marco teórico didáctico de este contenido, así como la forma en que se aborda. Para ello, se realiza un estudio sobre los conocimientos previos de los estudiantes, sus obstáculos para el aprendizaje y un análisis del locus de la investigación.
ii) Concepción y análisis a priori: Etapa en la que se delimitarán las variables (globales y locales) sobre las que puede actuar la docencia, como forma de orientar la investigación y elaborar un plan de acción. Según Santos y Alves (2017, p. 450), “las variables globales están destinadas a orientar las elecciones de investigación, mientras que las variables locales están dirigidas a predecir posibles comportamientos y obstáculos de los estudiantes, a través de situaciones didácticas”.
iii) Experimentación: Fase en la que se aplican las situaciones didácticas construidas, se firma el contrato didáctico y se realiza la recogida de datos.
iv) Análisis a posteriori y validación: Fase que se basa en todos los datos recopilados durante la etapa de experimentación. Luego del análisis de los datos recolectados, es necesario confrontarlos con el análisis a priori realizado inicialmente para validar (o no) las hipótesis formuladas en la investigación.
Según Almouloud y Coutinho (2008, p. 68), “El objetivo es relacionar las observaciones con los objetivos definidos a priori y estimar la reproducibilidad y regularidad de los fenómenos didácticos identificados”. Sin embargo, cabe señalar que cada fase se puede retomar, revisar y mejorar durante el transcurso de la investigación, ya que estas fases siempre están en construcción y mejora.
En el caso de este trabajo, por tratarse de una investigación en curso, caracterizada por una propuesta didáctica, nos limitamos aquí solo a las dos primeras fases de la Ingeniería Didáctica.
Análisis preliminares
Según Almouloud y Silva (2012) los análisis preliminares traen consideraciones sobre el marco teórico didáctico general, así como el análisis epistemológico de la enseñanza actual de un determinado tema, las concepciones, dificultades y obstáculos de los estudiantes, y el análisis del campo de la restricciones y requisitos en los que se ubicará la efectiva realización didáctica.
Para el análisis preliminar de este trabajo, traemos el concepto de transposición didáctica desde la perspectiva de Chevallard (1991) y, a partir de este concepto, buscamos relacionarlo con los obstáculos en la enseñanza de las cuádricas dentro del campo de la Geometría Analítica. De esta manera, desde una concepción epistemológica y didáctica, buscamos presentar una propuesta didáctica utilizando GeoGebra 3D como alternativa para la transposición didáctica del tema mencionado.
Transposición Didáctica
La transposición didáctica, según Chevallard (1991), permite la transformación del saber científico en saber a enseñar, posibilitando una mediación entre estos saberes para facilitar la comprensión del estudiante. Las diferentes formas en que pueden ocurrir las transformaciones brindan un abanico de posibilidades metodológicas para el docente. El autor presenta la siguiente definición de transposición didáctica:
Un contenido de conocimiento que se ha definido como saber a enseñar, sufre, a partir de entonces, un conjunto de transformaciones adaptativas que le permitirán ocupar un lugar entre los objetos didácticos. El 'trabajo' que convierte un objeto de conocimiento en enseñanza, un objeto de enseñanza, se llama transposición didáctica. (Chevallard, 1991, p. 39, nuestra traducción).
Según Chevallard (1991) existe una diferencia entre lo que se desarrolla en espacios puramente científicos y lo que se desarrolla en entornos educativos. Así, para que la enseñanza del conocimiento sea posible, éste sufrirá cambios que permitan enseñarlo. La idea central es que, para el desarrollo de la práctica docente, siempre es necesario establecer prioridades en la difusión o propagación de los procedimientos educativos.
Así, la noción fundamental es la existencia de una necesidad imprescindible de adecuar los conocimientos a las diversas cuestiones relacionadas con la situación escolar: el tiempo y espacio disponible, el tamaño del grupo de estudiantes, sus niveles, sus proyectos, su relación con el conocimiento, el contrato didáctico vigente, la relación pedagógica, así como los requisitos de evaluación.
Sin embargo, la transposición didáctica se da en la relación entre distintos elementos que componen la relación didáctica - el docente, el alumno y el saber -, siendo un trabajo de transposición interna, que se da dentro del sistema educativo. Esta relación ternaria se denomina sistema didáctico y compondrá el esquema fundamental del proceso de transposición didáctica de Chevallard (1991, p. 23):
Figura 1: El sistema didáctico, según Chevallard
Fuente: Chevallard (1991, p. 23)
La figura 1 presenta, además de los elementos que componen el sistema didáctico - docente (enseignant), alumno (apprenant) y el saber (savoir) - las interacciones que existen entre ellos. En este sentido, no existe jerarquía, posición de poder o distinción, sino una relación en la que cada elemento del sistema tiene una función y relevancia única. De esta forma, el conjunto de sistemas didácticos constituirá el sistema de enseñanza, el cual presenta una asociación de dispositivos estructurales que permiten el funcionamiento didáctico.
El sistema educativo trae consigo las relaciones binomiales alumno-saber, profesor-saber y profesor-alumno según Chevallard (1991), que comprenden elementos como concepciones y obstáculos, así como estrategias de apropiación del conocimiento -relación alumno-saber-, la propia transposición didáctica y la elaboración de contenidos -relación docente-saber- y el contrato didáctico preestablecido (Brousseau, 2008) para que el funcionamiento de una situación didáctica se dé de manera eficiente - relación profesor-alumno.
Según Chevallard (1991), una de las prioridades de la transformación en el tratamiento que se le da al conocimiento en un proceso de transposición didáctica es, sin duda, la selección de contenidos que constituirán un programa escolar y que, en su totalidad, formar saberes escolares, teniendo como fuente originaria el saber científico. Para que este conocimiento científico se transforme en conocimiento escolar, pasará por un proceso de diversas modificaciones influido por diferentes partes del sistema educativo.
Comúnmente, el contenido de las cónicas, que es un requisito previo para la comprensión de las superficies cuádricas, es poco o rara vez estudiado en la Educación Básica en las escuelas brasileñas, causando dificultades para los estudiantes cuando ingresan a los cursos de grado y se enfrentan a las disciplinas de Geometría Analítica, Cálculo Diferencial e Integral, entre otras situaciones que necesitan de este conocimiento, además de dificultar su evolución en la comprensión de las superficies en el espacio y sus aplicaciones.
Souza et al. (2020) señala que existe un desajuste entre lo que durante años han defendido los docentes, las matrices curriculares y los documentos oficiales, sobre la necesidad de desarrollar el razonamiento lógico-deductivo y la realidad práctica en el aula, tanto en la Educación Básica como en los cursos de grado en matemáticas.
Para ello, sería interesante que el profesor abordara las cónicas y, posteriormente, las cuádricas dentro del aula con un software de geometría dinámica. Sin embargo, la realidad es que muchos docentes tienen dificultades para utilizar estos recursos. Según Stols y Kriek (2011), el comportamiento real de muchos docentes en relación con el uso de software está influenciado por la utilidad percibida de la tecnología o por su capacidad para facilitar su trabajo en el aula. Sin embargo, si los maestros no dominan la tecnología para usarla en el salón de clases, no se usará. Por lo tanto, destacamos que es importante que los profesores analicen las posibilidades de enseñanza utilizando tecnologías en la planificación de sus clases, con el objetivo de una transposición didáctica eficiente, promoviendo el aprendizaje de una clase más dinámica.
De esta manera, relacionando lo expuesto con el tema de este trabajo, la transposición didáctica del contenido de las cuádricas permea el campo epistemológico, requiriendo una comprensión desde sus fundamentos matemáticos desde el punto de vista histórico y algebraico, discutidos en la sección siguiente.
El concepto de cuádricas en Geometría Analítica y GeoGebra
Respecto a lo que actualmente llamamos cuádricas, existen aportes significativos de los matemáticos helenos Apolonio y Pappus. Apolonio de Perge (262 (?) - 190 (?) a. C.), quien se supone que estudió y durante algún tiempo enseñó en la “Universidad de Alejandría”, mostró en su obra por primera vez que la elipse, la parábola y la hipérbola podrían obtenerse variando la pendiente del plano de sección sobre un cono de dos hojas. Para regocijo de muchos, su obra “As conicas” quedó casi ilesa: de sus ocho libros, solo uno se perdió (Venturi, 2013).
Pappus (siglo IV dC) vivió cuando las matemáticas griegas tomaban sus últimos respiros. Escribió la Colección de Matemáticas, que desafortunadamente fue un “réquiem de las matemáticas griegas, porque después de Pappus, las matemáticas se marchitaron y casi desaparecieron, y tuvieron que esperar 1300 años para un renacimiento a principios del siglo XVII” (Simmons, 1987).
Sin embargo, como trae Venturi (2013), le debemos a Leonhard Euler (1707-1783) una de las contribuciones más significativas a la Geometría en E³. En su libro Introductio in Analysin Infinitorum (Introducción al Análisis Infinita, publicado en 1748), Euler presenta la primera exposición de libro de texto de cuádricas, considerándolas como superficies de segundo grado en E³. En ese libro, Euler presenta las ecuaciones de conos, paraboloides, elipsoides e hiperboloides utilizando el sistema cartesiano en E³.
Sin embargo, para comprender las cuádricas, es necesario pasar por una comprensión de las cónicas, que son un requisito previo para su comprensión.
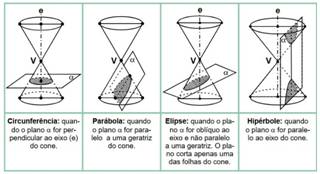
Según Venturi (2003, p. 119) “La palabra cónica (o sección cónica) proviene del hecho de que dicha curva se obtiene cortando un plano α sobre el cono circular recto”. También según el autor, cuando el plano α es secante al cono y no contiene el vértice, se puede utilizar un círculo, una parábola, una elipse o una hipérbola como sección cónica, como se ilustra en la Figura 2:
Figura 2: Cónicas formadas por la sección de un plano α sobre un cono circular recto.
Fuente: Venturi (2003, p. 119).
En caso contrário, el “conjunto de puntos del plano cuyas coordenadas cartesianas satisfacen una ecuación de 2º grado con dos variables” se denomina cónico ”(Venturi, 2003, p. 120), del tipo:
siendo esta una ecuación completa cuando todos sus coeficientes no son nulos.
El término 𝐵𝑥𝑦, cuando 𝐵 ≠ 0, muestra que el eje focal de la cónica es oblicuo a los ejes cartesianos. La ecuación descrita 𝐴 𝑥 2 +𝐵𝑥𝑦+𝐶 𝑦 2 +𝐷𝑥+𝐸𝑦+𝐹=0 puede ser una elipse, una hipérbola o una parábola, dependiendo del valor del discriminante 𝐵 2 −4𝐴𝐶. Siel discriminante es igual a cero, hay una parábola; si es menor que cero, hay una elipse; si es mayor que cero, hay una hipérbola. Y, si 𝐵=0 y 𝐴=𝐶, la ecuación representa una circunferencia.
Para obtener la ecuación canónica de 𝐴 𝑥 2 +𝐵𝑥𝑦+𝐶 𝑦 2 +𝐷𝑥+𝐸𝑦+𝐹=0, se deben eliminar los términos de 1° grado y/o 2º grado y luego se debe aplicar la traslación o rotación de los ejes (Venturi, 2003),según el orden de transformaciones que se muestra en la Figura 3:
Figura 3: Orden de las transformaciones
Fuente: Venturi (2003, p. 121)
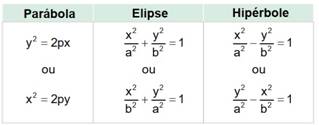
Al obedecer tales órdenes de transformación, recurrimos a las ecuaciones canónicas de las cónicas, como se ilustra en la Figura 4:
Figura 4: Ecuaciones canónicas de las cónicas
Fuente: Venturi (2003, p. 121)
En su forma canónica, las cónicas tienen elementos para su descripción como vértice, eje focal, foco, directriz, distancia focal, entre otros. Según Bermúdez y Mesa (2018), estos elementos son intrínsecos y no dependen de un sistema de referencia o sistema de coordenadas, ya que pertenecen a la estructura matemática. Es de destacar que, desde un punto de vista didáctico, todas las definiciones de cónicas se basan en la distancia entre dos puntos, que se puede expresar en el plano 𝑥𝑂𝑦, a través del Teorema de Pitágoras.
En cuanto a las superficies en Geometría Analítica, Fermat ya apuntaba en sus estudios sobre las posibilidades de una tercera dimensión. Según este matemático “Si el problema propuesto involucra tres incógnitas, se debe encontrar, para satisfacer la ecuación, no solo un punto o una curva, sino toda una superficie” (Venturi, 2003, p. 161).
En lenguaje matemático, las cuádricas se pueden definir, según Venturi (2003), por un conjunto de puntos en el espacio tridimensional (E³), en la que sus coordenadas cartesianas resultan una ecuación de 2º grado a, como máximo 3 variables, siendo descrita por la ecuación cartesiana de la superficie cuádrica:
dónde A, B, C, D, E, F, G, H, I y J son números reales, siendo al menos uno de los coeficientes A, B, C, D, E y F no nulo. El término independiente J, cuando es nulo, configura una cuádrica que pasa por el origen, ya que el punto 𝑂=(0,0,0) satisface esta ecuación.
Sin embargo, no profundizaremos en este trabajo en el estudio general de las superficies dadas por esta ecuación general, sino que nos acercaremos a las cuádricas en su forma canónica. Para estudiarlos, analizaremos sus secciones planas Q ∩ π, donde π es un plano paralelo a uno de los ejes de coordenadas.
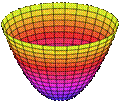
Las cuádricas pueden considerarse el resultado de rotar una cónica alrededor de un eje. Esferas, paraboloides, elipsoides, hiperboloides, cilindros de segundo grado y conos son las superficies cuádricas más comunes. El Cuadro 1 resume los coeficientes y el lugar geométrico originado por algunas posibles situaciones que se pueden construir a partir de la propuesta de este trabajo, para ser exploradas más adelante, en el análisis a priori:
Cuadro 1: Lugar geométrico y tipos de superficies cuádricas
Coeficientes (A, B e C)
Lugar Geométrico
Todos Positivos
Elipsoide
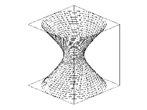
Dos positivos y uno negativo
Hiperboloide de una hoja
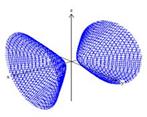
Uno positivo y dos negativos
Hiperboloide de dos hojas
Coeficientes (A e B)
Lugar Geométrico
Mismo signo
Paraboloide Elíptico
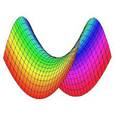
Signos opuestos
Paraboloide Hiperbólico
Un cero
Superfície Cilíndrica Parabólica Recta
Fuente: Vargas e Leivas (2019, p. 40)
Cabe mencionar que es importante indagar en los conocimientos geométricos relacionados con las cuádricas, pues es una realidad que esta temática es poco o nada desarrollada en los programas de formación inicial del profesor de Matemáticas. El tema de cuádricas, cuando se trabaja en el grado en Matemáticas, en ocasiones prioriza los aspectos algebraicos en detrimento de los aspectos visuales y las representaciones geométricas. (Vargas & Leivas, 2019).
Así como Vargas y Leivas (2019), la autora Londero (2017) trae en su investigación un relevamiento que concluye que el estudio de las cuádricas en las graduaciones de Matemáticas se da de manera superficial y con un enfoque básicamente algebraico, lo que genera dificultades en la comprensión de las relaciones entre los aspectos algebraicos y geométricos que involucran cada una de las superficies cuádricas, así como la comprensión de estas relaciones entre las distintas cuádricas sometidas a un mismo sistema de referencia cartesiano.
El tema de las cuadráticas es de gran relevancia para el estudiante de Matemáticas, así como de áreas afines, ya que se comprueba su aplicación cotidiana en Ingeniería, Medicina, Física, entre otras áreas, siendo necesaria una modernización de las técnicas de enseñanza de este tema “para que el alumno pueda establecer relaciones entre estas áreas de las Matemáticas, interpretando geométrica y algebraicamente” (Vargas & Leivas, 2019, p. 45).
Como señala Richit (2005), la enseñanza de la Geometría Analítica debe ser capaz de desarrollar en el estudiante la habilidad de resolver un problema geométrica y algebraicamente, siendo necesario que el docente esté preparado para desarrollar en sus alumnos la habilidad de interpretar un problema o construcción gráfica desde la perspectiva del Álgebra y la Geometría, en efecto. Aún en la investigación de Richit (2005), la autora destaca la importancia de potenciar el estudio de la Geometría Analítica con el uso de tecnologías educativas, como los softwares de Geometría Dinámica.
Para ello, GeoGebra cuenta con recursos que permiten animación, visualización 3D, visualización por transparencia, que posibilitan aumentar el nivel de abstracción del alumno, desarrollando su percepción geométrica a través de la visualización.
La búsqueda de metodologías didácticas que posibiliten que los alumnos aprendan Geometría Analítica ha sido objeto de numerosos trabajos. Abar (2020) corrobora el pensamiento de Chevallard cuando señala que el desarrollo de las tecnologías, así como su introducción en el aula y en los entornos formativos, se acompaña de fenómenos del mismo orden que los de la transposición didáctica, destacando la relevancia del GeoGebra como un recurso para que esta transposición didáctica se produzca con eficacia. Sousa et al. (2021, p. 96) señalan que GeoGebra 3D es un recurso importante porque “permite una visualización tridimensional, brindando oportunidades para experimentar y construir conceptos geométricos”.
Fischbein (1993) señala que existen varias razones por las cuales la Geometría es tan difícil de insertar en los programas escolares y, entre ellas, es que los conceptos figurativos no se desarrollan naturalmente hacia su forma ideal. Es decir, las dificultades de los estudiantes para comprender conceptos geométricos también forman parte de una dificultad en la visualización mental del objeto, con sus características y propiedades. Y en muchos casos tales vergüenzas en el campo de la Geometría se extienden desde la educación básica hasta la educación superior.
Con base en lo anterior, se presenta en el análisis a priori un modelo matemático para ser explorado visualmente en el software GeoGebra, donde existe la posibilidad de asociar las formas canónicas de las cuádricas y sus respectivas formas gráfico-geométricas presentadas en formato 3D, siendo una propuesta didáctica para considerar por el profesor de Matemática, en vista de la transposición didáctica de este tema.
Análisis a priori
Artigue et al. (1995) señala que un análisis a priori busca precisar las posibilidades seleccionadas (entre las situaciones que se ponen en juego en el proceso experimental), los valores de las variables didácticas (microdidácticas o macrodidácticas) que se producen a partir de esta selección y el significado que pueden tener los comportamientos esperados, teniendo en cuenta estos valores. Almouloud (2012, p. 27) reitera que en el análisis a priori es posible hacer una predicción de comportamientos y “tratar de demostrar cómo el análisis permite controlar sus significados y asegurar, particularmente, que si ocurrieron tales comportamientos esperados, es como consecuencia del desarrollo orientado al aprendizaje”.
En esta etapa de ID, presentamos una propuesta de didáctica para la enseñanza de cuádricas con GeoGebra 3D, utilizando sus recursos visuales y manipulables, donde se parte de la premisa de que la exploración visual y la manipulación algebraica/geométrica de esta construcción está diseñada como elemento rector en la mediación didáctica del docente al trabajar con el tema mencionado. Según Alves (2020, p. 340) “el docente puede valorar el papel de la visualización, al explorar el software GeoGebra, con miras a adquirir una cultura matemática y perfilar hábitos intelectuales aplicables en otras situaciones”.
Alves y Dias (2019, p. 6) destacan que “la ED es una metodología de investigación, por lo que es fundamental el uso de teorías que sirvan de apoyo a la investigación y para la lectura/interpretación de datos posiblemente producidos por los estudiantes”. Así, se refuerza que el docente explore una teoría didáctica compatible con la planificación de contenidos y los objetivos a alcanzar en clase, como forma de orientar su trabajo.
Para trabajar de forma articulada con ID en este artículo traemos la Teoría de las Situaciones Didácticas (TSD) (Brousseau, 2008) como forma de organizar y modelar una situación didáctica que involucra el tema a partir de una construcción elaborada en GeoGebra, buscando predecir conductas a través de la situación propuesta.
Brousseau (2008, p. 20) define que “una 'situación' es un modelo de interacción de un sujeto con un entorno dado”. Partiendo de esta premisa, el término “situaciones didácticas” se refiere a modelos que describen la relación de actividades entre alumno, docente y el milieu. A grandes rasgos, tenemos que “el término 'milieu' indica el entorno no didáctico, un sistema antagónico, sin intención didáctica explícita y externo al alumno, que puede abarcar, entre otros, situaciones problema, juegos, saberes de los compañeros y del maestro” (Pommer, 2008, p. 5).
En resumen, TSD enfatiza el desarrollo del estudiante de manera activa y autónoma y puede ser modelado por fases o dialécticas según Brousseau (2008) pueden describirse, en resumen, por:
Situación de acción: es el momento de tomar posición, donde el estudiante tiene el primer contacto con la pregunta/problema y busca en sus conocimientos previos encontrar elementos necesarios para desarrollar posibles caminos a la solución.
Situación de formulación: etapa en la que se produce un intercambio de información entre el milieu y el alumno; es el momento de presentar las ideas de forma clara y verbal, pero sin ninguna formalización rigurosa. El alumno plantea estrategias y comienza a apropiarse de conocimientos.
Situación de validación: el alumno demuestra su estrategia a sus compañeros y al docente (mediador), buscando convencerlos de sus argumentos y validar su respuesta dentro del sistema previamente establecido.
Situación de institucionalización: el momento en que el docente sintetiza significativamente todo lo expuesto en las etapas anteriores, formalizando el carácter matemático de lo validado por los estudiantes.
Por lo tanto, la situación didáctica puede ser percibida como una situación en la que prevalece la dialéctica de la circunstancia y el contexto, y es fundamental que el docente haga el vínculo entre sus etapas y la transposición didáctica, como una forma de garantizar que los objetivos se alcancen en el salón de clases planeado. Cabe mencionar quepara la comprensión y desarrollo del estudiante en la situación didáctica aquí propuesta, es necesario que este estudiante tenga conocimientos previos sobre cónicas y una noción de superficies en el espacio.
Así, para articular ID y TSD, posibilitando la transposición didáctica del contenido de cuádricas, se presenta la siguiente situación propuesta:
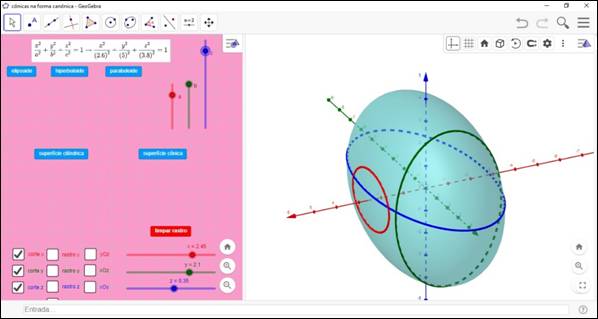
Situación didáctica: Haga clic en el botón elipsoide para que la superficie cuádrica se muestre en la ventana gráfica 3D y manipule los controles deslizantes a, b y c para que tomen valores diferentes. ¿Qué sucede con el elipsoide cuando se manipula el control deslizante a? ¿Y cuando los otros dos son manipulados? ¿Existe alguna relación entre los valores de los controles deslizantes a, b y c y los ejes del elipsoide? ¿Si sí, cuál?
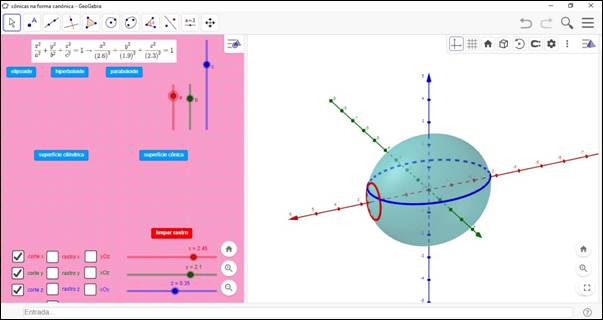
La construcción referente a la propuesta didáctica presentada se encuentra en la dirección electrónica https://www.geogebra.org/m/v3sehapj. Un fragmento de su exploración visual se presenta en la Figura 5:
Figura 5: Exploración de las cuádricas en forma canónica en GeoGebra 3D
Fuente: Elaboración de los autores (2021)
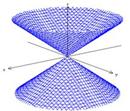
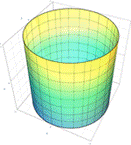
En la situación de acción, se espera que el estudiante, desde la construcción, observe cuidadosamente todos los elementos disponibles en la ventana de visualización del lado derecho de la pantalla, como se muestra en la Figura 5, encontrando los tipos de superficies cuádricas disponibles: elipsoide, paraboloide e hiperboloide (con 1 o 2 hojas) y a partir de una visión general, buscarsus conocimientos previos sobre los conceptos necesarios para el análisis de la pregunta.
Así, se pretende que el alumno, desde su posición inicial, explore la construcción a partir de los comandos dados, es decir, manipulando los deslizadores a, b y c, en los que cada uno cambia el formato del gráfico de forma diferente, como ilustrado en las Figuras 6, 7 y 8:
Figura 6: Manipulación del control deslizante 𝑎
Fuente: Elaboración de los autores (2021)
Figura 7: Manipulación del control deslizante 𝑏
Fuente: Elaboración de los autores (2021)
Figura 8: Manipulación del control deslizante 𝑐
Fuente: Elaboración de los autores (2021)
En la situación de formulación, el alumno deberá anotar sus observaciones y las relaciones que se establecen entre el formato visual de cada una de las cuádricas con su respectiva ecuación canónica, buscando comprender la diferencia entre cada una de estas ecuaciones.
En la situación de validación, es importante que el estudiante verbalice lo que observó de la manipulación de los deslizadores a, b y c, verificando el cambio en los coeficientes de las ecuaciones de las superficies cuádricas y relacionando esta manipulación con los ejes de coordenadas.
Así, se espera que el estudiante argumente, por ejemplo, que al manipular el control deslizante a, hay un cambio en el elipsoide relacionado con el eje x; al manipular el control deslizante b, se cambia el elipsoide relacionado con el eje y, e; al manipular el control deslizante c, este cambio se relaciona con el eje z. También queremos que el alumno se dé cuenta de que al menos uno de los coeficientes a, b o c es diferente de cero para que pueda representar una superficie cuádrica. Y que si la superficie cuádrica está cortada por los planos coordenados o por planos paralelos a ellos, la curva de intersección será una cónica.
A partir de esta posible validación, el docente, en situación de institucionalización, debe presentar, con el debido rigor matemático y lenguaje formalizado, una síntesis de lo expuesto por los estudiantes, haciendo correcciones de modelos erróneos. Así, con base en lo anterior, contamos con un cuadro de síntesis (Cuadro 2) que explica la relación de las superficies cuádricas con sus respectivas fórmulas y representaciones gráficas y que puede ser presentado en el momento de la institucionalización, como una forma de retomar lo discutido anteriormente:
Cuadro 2: Relación entre superficie cuádrica, fórmula y representación gráfica.
Superficie cuádrica
Fórmula
Representación gráfica
Elipsoide
Elipsoide de revolución (caso particular del elipsoide)
Esfera (caso especial del elipsoide de revolución)
Paraboloide elíptico
Paraboloide de revolución (caso particular del paraboloide elíptico)
Paraboloide hiperbólico
Hiperboloide de una hoja
Hiperboloide de dos hojas
Cono
Cilindro elíptico
Cilindro circular (caso particular del cilindro elíptico)
Cilindro hiperbólico
Cilindro parabólico
Fuente: Elaboración de los autores (2021).
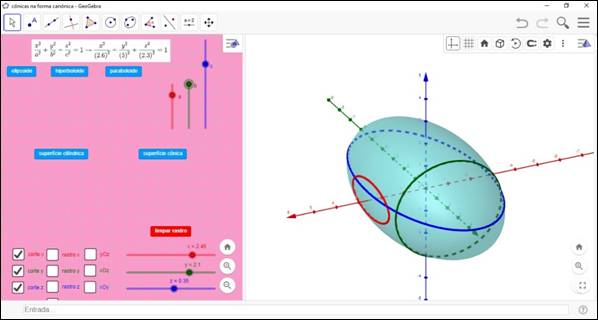
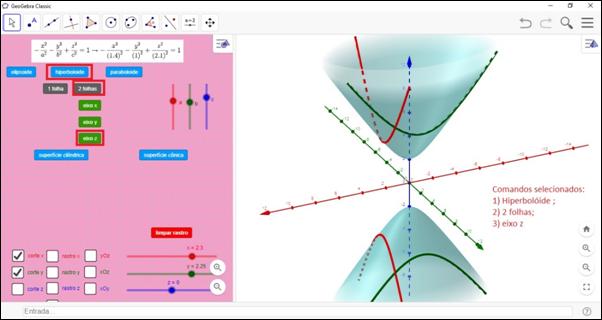
La construcción presentada en este análisis a priori puede explorarse de otras maneras. Existe la posibilidad de elegir otro tipo de superficie cuádrica para trabajar y explorar visualmente, como se puede observar en las Figuras 9 y 10:
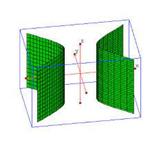
Figura 9: Hiperboloide de dos hojas
Fuente: Elaboraciónde los autores (2021)
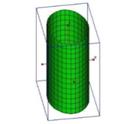
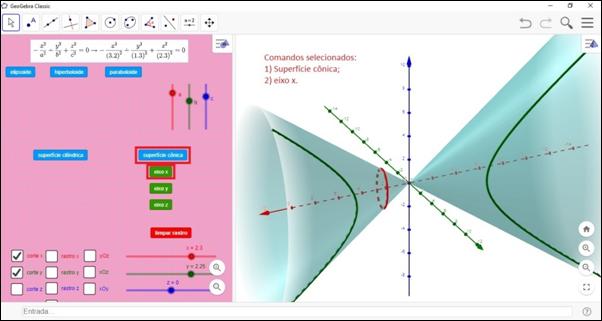
Figura 10: Superficie cónica en el eje x
Fuente: Elaboración de los autores (2021).
Nótese que, en la Figura 9, se presentó la posibilidad de construir un hiperboloide de dos hojas sobre el eje z, mientras que en la Figura 10 es posible visualizar una superficie cónica construida sobre el eje x. Por lo tanto, los controles deslizantes a, b y c permiten la manipulación de los coeficientes de las ecuaciones de superficie, que están en forma canónica. Haciendo clic en opciones 𝑦𝑂𝑧, 𝑥𝑂𝑧 o 𝑥𝑂𝑦 los planos paralelos a los planos de coordenadas se muestran desplazándolos desde la manipulación del control deslizante correspondiente (𝑥,𝑦 o 𝑧). Es posible visualizar las curvas correspondientes a la intersección de la cuádrica con estos planos haciendo clic en los botones de recorte y mostrar el rastro que dejan estas curvas cuando se mueve el control deslizante correspondiente con la opción de rastro seleccionada.
Fischbein (1993), sobre el dominio de la geometría y su relación con la visualización, reitera que una de las principales tareas de la educación matemática es crear tipos de situaciones didácticas que sistemáticamente soliciten una estricta cooperación entre concepto e imagen, hasta su fusión en objetos mentales unitarios. Por tanto, lo que se pretende con la situación didáctica que se propone en este trabajo es desarrollar en los estudiantes, a través de la visualización, la comprensión de los elementos pertenecientes a las cuádricas, así como la relación entre sus ecuaciones y sus respectivas formas gráficas en el ámbito de la Geometría Analítica, mediando la posibilidad de una adecuada transposición didáctica.
Así, en esta construcción existe la posibilidad de explorar visualmente las superficies cuádricas utilizando el software GeoGebra en su ventana 3D, permitiendo al docente ampliar la exploración de conceptos geométricos de forma paramétrica o implícita, así como los principales elementos que componen cada una de estas superficies.
Además, para un posible análisis y validación a posteriori, destacamos la posibilidad de replicar esta construcción como modelo a aplicar en situaciones-problema contextualizadas que involucren al sujeto y requieran una exploración visual, recolectando datos y confrontándolos con un modelo de análisis a priori previamente elaborado por parte del profesor a partir de la construcción aportada.
CONSIDERACIONES FINALES
Al realizar este trabajo, se percibió en el relevamiento epistemológico y didáctico sobre las cuádricas, la importancia de una planificación didáctica con miras a una transposición didáctica mejor elaborada y desarrollada de este tema, en el cual hay un camino a seguir en el estudio de esta área en una forma más dinámica.
Así, este trabajo busca contribuir, a partir de los análisis preliminares realizados, a la posibilidad de identificar los elementos principales de las curvas como la elipse, la parábola y la hipérbola, prestando atención a que estas son más amplias que las gráficas de funciones, y en el análisis a priori realizar la exploración de estas curvas, las cuádricas elipsoide, paraboloide e hiperboloide y sus variaciones, buscando instigar al estudiante de pregrado y futuro docente de Matemáticas en la búsqueda de conocimientos que sustenten su aprendizaje, demostrando funciones y propiedades de las cónicas y cuádricas,para ampliar este estudio para su uso con situaciones reales.
GeoGebra 3D, como recurso de manipulación y visualización geométrica, permite al estudiante analizar el comportamiento de las ecuaciones que se refieren a las cuádricas, entendiendo la naturaleza de cada una de sus variables a partir de su movimiento en la gráfica como en la construcción presentada en este trabajo, siendo un recurso que puede ser utilizado por el profesor de Matemáticas en el aula, como vía para posibilitar la enseñanza de esta asignatura.
Finalmente, se espera que la propuesta metodológica abordada en este trabajo pueda ser considerada por otros docentes como material didáctico para el trabajo de esta asignatura dentro del campo de las Matemáticas. Como es una investigación en curso, la recolección de datos de esta aplicación ocurrirá en la investigación de maestría, realizada con estudiantes de pregrado en Matemáticas, para ser presentado en una perspectiva de trabajo futuro.