ÁREA: INGENIERÍA Y TECNOLOGÍA

Comparación entre Modelos en Diferencias Finitas Aplicados a la Infiltración en Suelos

Comparison of Finite Difference Models Applied to Soil Infiltration

 

Hector A. Pedrozo^{1 *}, Mario R. Rosenberger¹, Carlos E. Schvezov¹

¹ Instituto de Materiales de Misiones (IMAM) CONICET, Universidad Nacional de Misiones, Félix de Azara 1552, CP 3300, Posadas, Misiones, Argentina.
* E-mail: pedrozoalejandro91@gmail.com

---

Resumen

La infiltración es el proceso por el cual penetra agua en un medio poroso, está descripta por la ecuación de Richards. Esta ecuación y las ecuaciones constitutivas asociadas son marcadamente no lineales. En este trabajo se resuelve la ecuación de Richards usando distintas aproximaciones en diferencias finitas, se analiza la velocidad de cálculo y la sensibilidad en los resultados para diferentes valores de paso de tiempo.
Para la resolución se utilizaron tres métodos de cálculo; método explícito (ME), método implícito simple (MIS) y el método de Crank-Nicolson (MCN). En el problema planteado, se tomaron condiciones de frontera de Dirichlet.
Se obtuvo que los tres modelos convergen a la misma solución por el análisis de sensibilidad para la variable ?t y que el modelo de Crank-Nicolson presenta los menores errores relativos en la zona del frente húmedo, el que a pesar de su mayor complejidad, requiere un tiempo de cómputo reducido.

Palabras clave: Métodos numéricos; Ecuación de Richards; Medios porosos; Métodos implícitos; Métodos explícitos.

Abstract

Infiltration, that is the process by which water enters a porous medium, is described by Richards' equation. This equation and the associated constitutive equations are markedly nonlinear. In the present research work, Richards' equation is solved by using different approximations in finite differences, and by analyzing the calculation speed and the result sensitivity for different time step values they are compared.
Three different methods of calculation were used to solve it: the explicit method (ME), the simple implicit method (MIS) and the Crank-Nicolson method (MCN). In the present work, Dirichlet boundary conditions were taken.
It was found that the three models converge to the same solution for the sensitivity analysis of the ?t variable and the Crank-Nicolson's model has the lowest relative errors in the area of the wet front which, despite its complexity, requires reduced computation time.

Keywords: Numerical methods; Richards' equation; Porous media; Implicit methods; Explicit methods.

---

 

Introducción

El proceso de infiltración tiene importancia para el desarrollo de investigaciones relacionadas a los recursos hídricos necesarios para el desarrollo de las plantas. A la vez mediante este proceso se puede estimar el contenido de humedad del suelo, ya que de esta variable depende la difusión de especies químicas, y de esta forma adoptar las prevenciones necesarias para disminuir la contaminación de este medio.
Se diferencian dos regiones importantes en el suelo, la zona saturada, en la que la humedad en el medio es máxima, y la zona no saturada donde la humedad del suelo no es máxima. Estas se encuentran divididas mediante el nivel de agua freática, donde la presión hidrostática es igual a la presión atmosférica ^[1].
En la zona no saturada se han diferenciado 4 fases: sólido, aire, agua y la interface agua-aire. Esta interface induce una succión mátrica en los poros del suelo, dicha succión afecta la fuerza y las características del cambio de volumen en suelos no saturados ^[2]. En la zona saturada los poros del suelo se encuentran llenos de agua, por lo que se encuentran a la presión hidrostática.
Para un proceso unidimensional de infiltración en un suelo isoentrópico, las variables de entrada son el tiempo y la profundidad, y las relaciones constitutivas son la conductividad hidráulica y la capacidad específica. La variable de salida es el potencial mátrico o la humedad volumétrica dependiendo de la ecuación utilizada. Los gradientes de potencial mátrico y del potencial gravitacional son las fuerzas principales que intervienen en el fenómeno de transporte del fluido.
En el presente trabajo se parte de la ecuación de Darcy para describir la infiltración. Esta define el caudal por unidad de área en función de la conductividad hidráulica y el gradiente espacial de potencial mátrico. Esta ecuación solo tiene aplicabilidad directa para la zona saturada del suelo, en la cual la humedad en el medio es máxima. Para la zona no saturada, el proceso es descripto por la ecuación de Richards, la cual se obtiene de la combinación de la ecuación de Darcy y la ecuación de continuidad para el volumen de control dado.
El drenaje en suelos saturados y no saturados es estudiado debido a su importancia para el correcto diseño de la sustentación de obras de edificación; y dada la forma compleja del proceso de infiltración, los modelos usados para representar su comportamiento reflejan dicha complejidad ^[3]. En este trabajo se proponen distintos métodos para la solución de este problema, y se busca lograr el compromiso entre error cometido del modelo y tiempo de cómputo necesario.
Se encuentra una mayor complejidad en la zona no saturada por las variaciones no lineales de la conductividad y la capacidad con la humedad. Debido a esto, se propone la aplicación de métodos numéricos para la obtención de distintos modelos que resuelven el problema. Los modelos que se proponen son en diferencias finitas ya que tienen una formulación relativamente simple y pueden implementarse fácilmente. Además, como hacen un balance local en cada porción del dominio se tiene una buena precisión en el balance de masa.

Modelo matemático y ecuaciones de gobierno
La ecuación de Darcy en términos de potencial mátrico con coordenada vertical que crece hacia arriba, puede ser expresada unidimensionalmente como:

Para este proceso se tiene la siguiente forma de la ecuación de continuidad:

Se define la capacidad específica del suelo como:

La Ecuación de Richards se obtiene a partir de la combinación de las ecuaciones (1), (2) y (3):

Dónde q es el caudal por unidad de área, h es el potencial mátrico debido a la succión, t es el tiempo, z es la profundidad, K(h) es la conductividad hidráulica, ? es la humedad volumétrica del suelo, C(h) es la capacidad hidráulica específica del suelo.
Para describir la variación de la conductividad hidráulica y la capacidad hidráulica específica con respecto al potencial se utilizan las ecuaciones de Mualem-van Genuchten ^[4]:

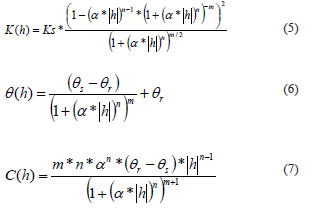
Donde ?s es la humedad volumétrica del suelo saturado, ?r es la humedad volumétrica residual del suelo, a, n, m son parámetros que dependen del suelo, Ks es la conductividad hidráulica saturada.

Modelo explícito
El modelo explícito (ME) se obtiene aproximando, en la ecuación de continuidad (Ec (2)), la derivada temporal de potencial por una diferencia hacia adelante y la derivada espacial del caudal se aproxima mediante una diferencia centrada.

Así, utilizando la ecuación de Darcy se aproximan los caudales en medio paso según las siguientes expresiones con diferencias hacia adelante o hacia atrás dependiendo el caso.

Reemplazando estos términos en la aproximación de la ecuación de continuidad y reagrupando se obtiene la siguiente expresión que describe el proceso:

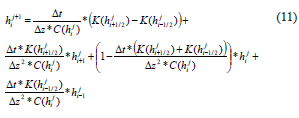
Esta es la ecuación general de un nodo para el modelo explícito que será utilizada más adelante para calcular la infiltración en el suelo.

Modelo Implícito
El modelo implícito simple (MIS), como en el caso anterior parte de la ecuación de continuidad. Se aproxima la derivada temporal mediante una diferencia hacia adelante y la derivada espacial mediante una diferencia centrada, pero con los valores de caudal evaluados en un tiempo futuro.

Se estiman los caudales mediante las ecuaciones (9) y (10) reemplazando estos en la ecuación (12) se obtiene le siguiente expresión:

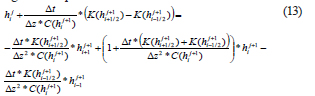
Esta es la ecuación general de un nodo para el modelo implícito simple que será utilizada más adelante para calcular la infiltración en el suelo

Modelo Crank-Nicolson
El modelo Crank-Nicolson (MCN) es implícito, y se aproxima la derivada temporal en un tiempo de medio paso mediante una diferencia centrada, mientras que la derivada espacial se aproxima tomando una media aritmética de las diferencias centradas del caudal en tiempos enteros continuos:

Se reemplazan los caudales por las ecuaciones (9) y (10) y se reagrupa para llegar a la siguiente expresión que se utiliza en el algoritmo:

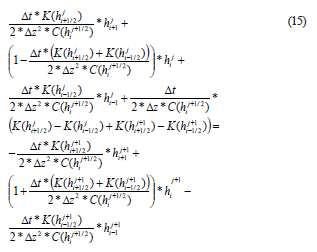
Esta es la ecuación general de un nodo para el modelo Crank-Nicolson que será utilizada más adelante para calcular la infiltración en el suelo.

Parámetros del suelo a medio paso
La forma de evaluar la conductividad hidráulica a medio paso tiene influencia en los perfiles de potencial obtenidos. Existen diferentes formas de evaluar este parámetro para pasos intermedios, como la media geométrica, media aritmética y media aguas arriba, sin embargo el valor correcto para esta conductividad intermedia es la media Darciana ^[8].
Para obtener la media Darciana se determina el caudal a medio paso, utilizando la media integral con los nodos como extremos, esto se puede ver en la ecuación (16).

En la ecuación de Darcy (Ec. (1)), se separan variables y se realiza la correspondiente integración, así se obtiene la ecuación (17).

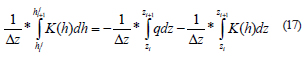
Se combinan las ecuaciones (9), (16) y (17) para obtener la ecuación (18), donde la conductividad hidráulica a medio paso que cumple con esta relación es la media Darciana.

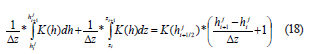
Como no se conoce la variación de la conductividad hidráulica con la profundidad, utilizar el valor exacto de la media Darciana es complejo, y más aun con las relaciones constitutivas utilizadas. Por esta razón, en este trabajo se supone variación lineal del potencial mátrico con respecto a la profundidad entre los nodos y se hace la aproximación de la ecuación (19).

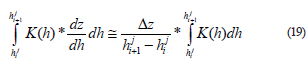
Combinando las ecuaciones (18) y (19), se obtiene la ecuación (20) que muestra la relación según la cual se calcula la conductividad hidráulica en posiciones intermedias a los nodos.
Así se justifica la utilización de una media integral, entre los nodos superior e inferior, para calcular el valor del parámetro en la posición intermedia. De esta forma se disminuyen los errores en las simulaciones, aun utilizando una malla relativamente gruesa.

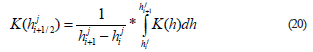
En el modelo Crank-Nicolson, la capacidad específica 1/2( ) j i C h + se calcula usando un valor de potencial calculado como la media aritmética entre los valores de paso de tiempo enteros contiguos.

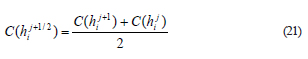
Procedimientos de cálculo
El modelo explícito (Ec. (11)) utiliza la conductividad y capacidad en el tiempo actual. Por otro lado, los modelos implícitos (Ec. (13) y (15)) utilizan la conductividad y capacidad a tiempos futuros, por lo tanto, se adopta un procedimiento de predicción corrección de dos etapas para usar en los modelos implícitos.
En el problema estudiado, el suelo inicialmente se encuentra a un valor de humedad uniforme, la condición de contorno inferior toma el mismo valor que la inicial y la condición de contorno superior es de valor especificado con humedad cercana a la de saturación. Por lo tanto, los valores de los nodos irán cambiando paulatinamente con el tiempo comenzando desde el contorno superior, eso significa que los nodos de la región inferior serán los últimos en cambiar.
Esta característica del problema permite que se pueda reducir el número de cálculos, de forma tal de identificar los nodos que cambiarían y los que no. Por lo tanto, todos los algoritmos, en cada paso de tiempo, buscan el nodo a mayor profundidad cuyo potencial es distinto de la condición inicial. Si se utiliza un modelo explícito se sabe que el nodo más profundo que puede cambiar de potencial es el nodo que se encuentra justo debajo del último nodo distinto de ) , 0(zh. Si se trata del modelo implícito simple o el modelo Crank-Nicolson, el nodo más profundo que puede cambiar es el que se encuentra dos posiciones por debajo de un nodo distinto a la condición inicial, ya que ambos modelos realizan dos etapas. La tolerancia utilizada para la búsqueda de los nodos distintos a la condición inicial es de 10-5, es decir que si un nodo tiene un sesgo, con respecto a la condición inicial, mayor que la tolerancia adoptada, se considera que el nodo cambió. De esta forma se reducen los cálculos realizados en cada paso del algoritmo.
Se construye una tabla evaluando la integral indefinida conductividad hidráulica-potencial mátrico para distintos valores de potencial. Con esta tabla se crea una función interpolante para obtener, en el algoritmo, los valores necesarios para calcular la conductividad hidráulica en posiciones intermedias. De esta forma se disminuye el tiempo de cómputo necesario para una simulación sin aumentar los errores en una forma significativa; y como el tiempo requerido para la creación de la tabla es despreciable no se incluye en la cuenta del tiempo de cómputo utilizado por el programa.

Implementación y Aplicaciones
Para la creación de los modelos propuestos se utilizó el software Wolfram Mathematica 8.0. Las simulaciones fueron calculadas en una computadora con procesador Intel® Core™ i3-2100 CPU@3.10GHz y 4 GB de memoria RAM. La comparación de los modelos se hizo tomando problemas de infiltración de agua en suelo que aparecen en la literatura.
Caso 1: La primera implementación posee las siguientes características del suelo y condiciones de contorno ^[5,6]:
?s= 0.368 m3 de agua*m-3 de suelo, ?r= 0.102 m3 de agua*m-3 de suelo, ?= 3.35 m-1, Ks = 9.22*10-5 m*s-1, n= 2, m= 1-1/n=0.5
Se aplican condiciones de frontera de Dirichlet: h(0, z)= -10 m que es el potencial mátrico en tiempo 0 para cualquier profundidad, h(t, 0)= -0.75 m que es el potencial mátrico en la profundidad 0 para cualquier tiempo, h(t, -1)= -10 m que es el potencial mátrico en la profundidad 1 m para cualquier tiempo.La profundidad del suelo es 1 m y el tiempo de simulación es de 1día. Para todos los casos se utilizarán 65 nodos, con lo que se obtiene ?z= -1/64 m.
Caso 2: En una segunda implementación del modelo se aplicó a resolver un problema de infiltración en suelos tomado de la bibliografía ^[5], donde las características del suelo y condiciones de frontera son las siguientes:
?s= 0.443 m3 de agua*m-3 de suelo, ?r= 0 m3 de agua*m-3 de suelo, ?= 4.49 m-1, Ks= 1.515*10-5 m*s-1, n= 3.6732, m= 1-1/n=0.727758.
Se aplica condiciones de frontera de Dirichlet: h(0, z)= -0.686524 m que es el potencial mátrico en tiempo 0 para cualquier profundidad, h(z, 0)= -0.062476 m que es el potencial mátrico en la superficie para cualquier tiempo, h(t, -1)= -0.686524 m que es el potencial mátrico en la profundidad 0.7 m para cualquier tiempo. La profundidad del suelo es 0.7 m y el tiempo de simulación es de 1.75 horas. Para todos los casos se utilizarán 65 nodos.
Para caracterizar los suelos de ambas aplicaciones se utilizan las curvas de retención de humedad, las cuales relacionan el contenido volumétrico de humedad con el potencial mátrico (Ec. (6)). Al analizar los suelos descriptos, comparándolas con datos que se encuentran en la bibliografía ^[7], la primera aplicación tiene características correspondientes a un suelo del tipo arenoso. Esto se puede ver en la Figura 1 debido a los bajos valores de humedad volumétrica saturada y residual que presenta, además del gran cambio de pendiente que se tiene en la figura. Por otro lado, la segunda implementación presenta una humedad saturada correspondiente a un suelo más arcilloso que la primera implementación, sin embargo presenta mayores cambios de pendiente, lo que se identifica con un suelo más arenoso. Por estas razones se estima que se trata de un suelo compuesto.

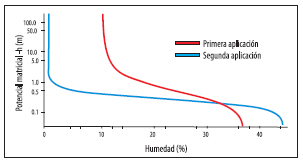
Figura 1: Curva de retención de los suelos

Resultados y discusión

Validación
En la Figura 2 se muestran los perfiles resultantes del proceso correspondiente a los datos de la primera y segunda implementación. Estas curvas fueron obtenidas mediante el modelo Crank-Nicolson (MCN). Como este es el modelo que se considera más exacto teóricamente ^[9] y presenta mayor convergencia, se utilizarán estos resultados como referencia para compararla con las otras simulaciones. Además, se consideran que los respectivos ?t son suficientemente pequeños, para obtener buenas aproximaciones a la solución de referencia adoptada.

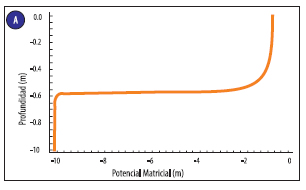
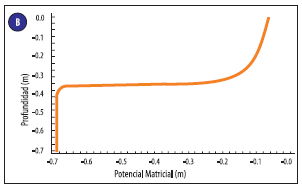
Figura 2: Curva de perfil de potencial obtenida con el modelo de Cranck-Nicolson, (a) para la suelo arenoso (caso 1) con un delta t=1s, (b) para la suelo compuesto (caso 2) para un delta t=0.1s.

En la Figura 2 se puede observar que existe una región donde se produce un gran cambio de potencial con un pequeño cambio de profundidad. Esta es la zona del frente húmedo y en este trabajo se define su posición exacta en el punto de inflexión de la curva de la Figura 2. Además, en el frente húmedo se tienen los mayores errores relativos, se estima que esto se debe a que la segunda derivada evaluada en la zona del frente húmedo es nula, por lo que la primera derivada es máxima, entonces el cambio de h con respecto a z también es máximo, y la diferencia entre conductividades en nodos continuos aumenta, que es un término presente en los errores de truncamiento de los modelos. También, se observa que la tercera derivada espacial para las distintas profundidades es máxima en el frente húmedo, y este es otro de los términos presente en el error de truncamiento de los modelos, estos motivos podrían explicar por qué se tienen altos errores relativos en esta zona.
Por estas razones, se considera apropiado que los modelos sean comparados en la zona del frente húmedo, tomando como medida el máximo error relativo entre dos perfiles obtenidos para las condiciones establecidas.
Para validar el modelo se utiliza la ecuación (22) para calcular el error relativo resultante en los perfiles obtenidos.

Donde j i h son los potenciales obtenidos de las figura 2 (el primer o el segundo caso según corresponda) y verdarero h son los potenciales que fueron obtenidos de gráficos en la bibliografía ^[5]. Sin embargo no se pudieron medir con total exactitud los potenciales tomados como verdaderos, teniéndose un error de medición de potencial de 0.05 m para el primer caso. Para el segundo caso, se estima un error de apreciación de 0.0068 m, y un error indeterminado en un intervalo alrededor del frente húmedo. Al realizar la comparación entre los datos de la bibliografía y los modelos propuestos se obtienen los gráficos de la Figura 3.

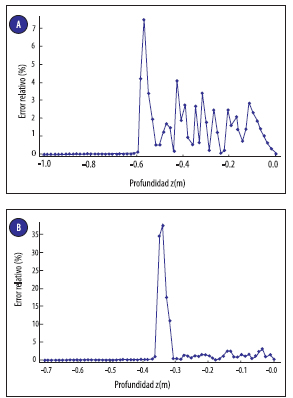
Figura 3: Error relativo versus profundidad entre datos de la bibliografía y el modelo propuesto. Suelo arenoso (a). Suelo compuesto (b).

Se puede ver en la Figura 3a, se tienen errores que varían en forma oscilante, estos en gran parte se deben al error de apreciación cometido en la medición de los datos de referencia. A medida que aumenta la profundidad el valor absoluto de h aumenta y los errores de apreciación se van haciendo cada vez menos importantes hasta que se llega a la zona del frente húmedo.
En el caso del suelo arenoso, esta comparación muestra un máximo error relativo de 7.52%, el cual se considera aceptable. También, se compararon los datos medidos con modelo explícito y modelo implícito simple. Para modelo explícito, se obtuvo un máximo error relativo de 7.98% para un paso de tiempo de 1 s y aumentando el error a medida que ?t aumenta; para modelo implícito simple un máximo error relativo de 7.06% para un paso de tiempo de 1 s, el error primero disminuye a medida que aumenta ?t al punto que los errores de estimación son más importantes, y luego aumenta con este.
En la Figura 3b también se tienen errores que varían en forma oscilante a bajas profundidades, sin embargo estos son pocos significativos comparados con el error que se produce en la zona del frente húmedo, donde el error de apreciación es máximo, alcanzando un 35%.

Comparación
En la Figura 4 se muestra la variación del máximo error relativo con respecto al paso de tiempo ?t para los tres modelos. Esta se obtuvo realizando simulaciones con cada modelo, utilizando diferentes pasos de tiempo y comparando con el resultado de referencia (ver Figura 2), correspondiente a cada implementación.

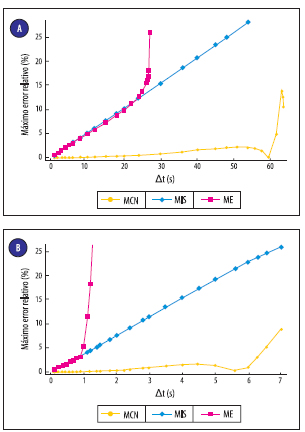
Figura 4: Máximo error relativo versus paso de tiempo. Suelo arenoso (a). Suelo compuesto (b).

Los resultados de las simulaciones se consideran aceptables y se incluyen en el gráfico si los valores de potencial obtenidos se encuentran entre los valores de las condiciones de contorno superior e inferior.
Se observa como el máximo error relativo representado en las figuras 4 a y b, el modelo Crank-Nicolson crece en forma aproximadamente lineal en ambos casos con una pendiente menor con respecto a los otros modelos, hasta un punto donde comienza a disminuir el error y luego vuelve a aumentar en mayor proporción.
Por otro lado, las pendientes del modelo implícito simple y modelo explícito son aproximadamente iguales para ambos casos, hasta un punto donde el modelo explícito crece en forma súbita, esto se corresponde con el fin de la zona de estabilidad del modelo explícito. Antes de este crecimiento, aunque los errores que se cometen en ambos modelos son aproximadamente iguales, en el modelo explícito se producen sobreestimaciones del potencial mátrico, mientras que el modelo implícito simple brinda subestimaciones del potencial. Este comportamiento podría atribuirse a la variación cuadrática de los errores de truncamiento con el paso del tiempo, debido a que los coeficientes de segundo orden de estos tienen diferentes signos.
En la Figura 5, se grafica el tiempo de cómputo frente al máximo error relativo para los tres modelos. Estas curvas resultan útiles para determinar el tiempo de cómputo necesario, dependiendo del error que se considere aceptable. Se destaca que los tiempos de computo necesarios para obtener los perfiles resultantes están el en orden de los segundos, este resultado se obtiene por los procedimientos más eficientes de cálculo de los modelos, como realizar los cálculos en cada paso solo con los nodos más cercanos a la superficies que tienen la posibilidad de cambiar en ese paso de tiempo.

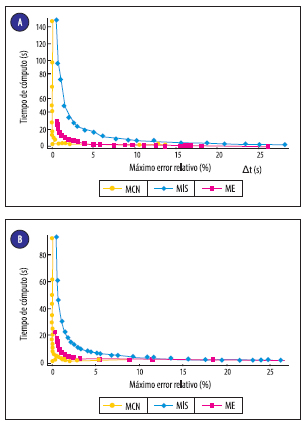
Figura 5: Tiempo de cómputo versus máximo error relativo Suelo arenoso (a). Suelo compuesto (b).

Se puede ver en la Figura 5 que, para los tres modelos el tiempo de cómputo varía en forma inversamente proporcional con el máximo error relativo. Sin embargo, la magnitud de cambio es diferente. El modelo Crank- Nicolson presenta gran convergencia, es por eso que tiene poco error al aumentar el paso de tiempo, esto disminuye el número de pasos y, por lo tanto, el tiempo de cómputo. Para cualquier error aceptable, el modelo Crank-Nicolson presenta menor tiempo de cómputo, seguido por el modelo explícito y por último el modelo implícito simple.

Estabilidad del modelo explícito
Se analiza el modelo explícito en función al paso de tiempo para encontrar el menor valor de esta variable para el cual, el modelo, se vuelve inestable. Para las condiciones de contorno planteadas y el tiempo total simulado, una simulación se considera estable cuando el mayor potencial mátrico se encuentra en los nodos más cercanos a la superficie, entonces se cumple que para todo i:

Para que el modelo sea consistente, el máximo valor que puede tomar 1 1 + jhes el valor de potencial de la condición de frontera superior, es decir j h0 , ya que este potencial no varía con el tiempo. Armando esta desigualdad y combinando con la ecuación (11) se obtiene la siguiente expresión:

El signo de desigualdad conserva ese sentido si y solo si el denominador es positivo. Como se debe cumplir la ecuación (23), este denominador debe ser positivo.
La ecuación (24) se utilizó para el suelo tipo arenoso para obtener los máximos valores de paso de tiempo crítico para distintos pasos de profundidad, ver Figura 6. En esta se puede ver que el ?t máximo no varía linealmente con el paso de profundidad. Además, este paso de tiempo critico se corresponde con el aumento de los errores para el modelo explícito en la Figura 4a.

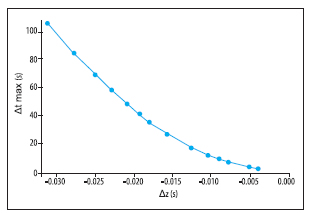
Figura 6: ?t máximo versus ?z, para el suelo tipo arenoso.

Para la primera aplicación, en el suelo arenoso se encontró que los valores críticos se corresponden al primer paso de tiempo, es decir que, si en el primer paso se cumplen las condiciones de estabilidad entonces se cumplen para pasos posteriores del modelo. Sin embargo para pequeños tiempos simulados se obtienen mayores errores en la zona del frente húmedo, que se van atenuando cuando aumenta la cantidad de pasos. Esto significa que el modelo es estable y el paso de tiempo crítico no depende del tiempo simulado.
Para el suelo compuesto, si se resuelve la ecuación (25), utilizando 65 nodos, se obtiene un paso de tiempo crítico de 2.44 s, pero realizando la simulación para un tiempo de 1.75 horas y comparando con el referente correspondiente (ver Figura 2b), se obtiene un error relativo de 229,5%. Esto significa que el paso de tiempo obtenido no es efectivo y la pérdida de la estabilidad no depende solo de los tres primeros nodos y las condiciones de frontera.
Se encontró que existe un valor de paso de tiempo crítico efectivo, que depende del tiempo de simulación, que si es superado se produce un gran aumento de pendiente en el gráfico del máximo error relativo versus ?t. Por lo tanto este valor máximo efectivo es encontrado como el punto donde se produce el cambio abrupto en la pendiente del gráfico de la Figura 4b, tal que ya no se cumple la ecuación (24) para todos los nodos.
En general, para cuando se trabaja con este tiempo máximo efectivo, ya se tiene que los errores aumentan con cada paso del modelo. Sin embargo, la acumulación de errores no es significativa hasta un tiempo de simulación dado, para dicho paso de tiempo.
Para analizar este fenómeno se desarrolló un código computacional, en el que ingresando el paso de tiempo y el paso espacial, se obtenga el tiempo simulado para el que ya no se cumple con la condición de la ecuación (24). Se presenta la información obtenida en forma gráfica en la Figura 7.

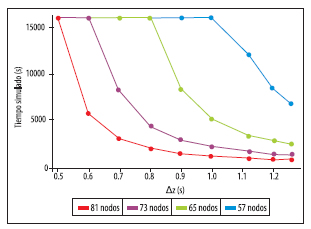
Figura 7: Tiempo de simulado versus ?t crítico para diferentes mallas uniformes.

En la Figura 7 se pueden observar los máximos tiempos de simulación para los cuales los valores de paso de tiempo se vuelven críticos para diferentes números de nodos tomados en la profundidad de 0.7 m. Se destaca que en la parte izquierda superior del gráfico, donde no existe gran variación del tiempo simulado para los diferentes números de nodos considerados, se debe a que el frente húmedo alcanzó la profundidad máxima del dominio donde se realiza la simulación, por lo que, en estos casos no significa la pérdida de estabilidad del modelo.
Se tiene que en todos los casos el paso de tiempo crítico efectivo disminuye a medida que aumenta el tiempo de simulación. Esto demuestra la inestabilidad del modelo para el suelo tipo compuesto, sin embargo se pueden obtener resultados aceptables si se trabaja en un entorno correcto de valores de pasos de tiempo y espacio, para el tiempo de simulación necesario.

Óptimo en el modelo Crank-Nicolson
Se puede ver en la Figura 4 que en el modelo Crank- Nicolson el error aumenta en forma paulatina con el paso de tiempo y luego comienza a disminuir hasta llegar a un mínimo desde donde vuelve a crecer en forma súbita. Este mínimo es un óptimo para la simulación debido a que se obtienen errores y tiempos de cómputo relativamente bajos.
El valor del paso de tiempo para el que se tiene este mínimo es independiente del tiempo simulado, aunque cuanto mayor es este, menor es el error que se comete, lo que quiere decir que el modelo tiende a estabilizarse. Por otro lado, este mínimo depende del valor de ?z utilizado.
Se ha observado, que para la etapa predictiva en el modelo Crank-Nicolson, trabajando cerca de este valor óptimo, se obtiene un resultado que no satisface la ecuación (24). Sin embargo, cuando el algoritmo realiza la etapa de corrección se obtiene el perfil con un error reducido, este fenómeno aun está pendiente de ser explicado.
No se encontró una forma de predecir el óptimo de esta función, por lo que el problema se continuará estudiando. Sin embargo, se estima que está relacionado con los errores de truncamiento del modelo, los cuales varían en forma cúbica con el paso de tiempo.

Conclusiones

Se compararon tres modelos en diferencias finitas para el trasporte de agua en suelo no saturado: un modelo explícito, uno implícito simple y uno de tipo Crank-Nicolson. Se aplicaron a dos tipos de suelos diferentes uno de características arenoso y otro de características compuestas.
Se analizó el máximo error relativo en el valor del potencial mátrico en la zona del frente húmedo y se encontró que:

I). en el modelo explícito es lineal a bajos valores de paso de tiempo y luego en un valor determinado se incrementa abruptamente, esto se identifica con el punto final de la zona de convergencia del modelo.
II). en el modelo implícito simple la relación es lineal y crece con la misma pendiente que en la zona lineal del modelo explícito.
III). en el modelo Crank-Nicolson la relación es casi-lineal con una menor pendiente que en los otros modelos, hasta alcanzar un mínimo óptimo con un incremento posterior.

Al comparar los errores versus tiempo de cómputo se encuentra que el modelo Crank-Nicolson tiene el menor error. Por ejemplo, para un error del 1% la demanda de tiempo de cómputo es de 5, 15 y 75 segundos para el modelo Crank-Nicolson, explícito e implícito simple, respectivamente, lo cual indica que el modelo Crank-Nicolson presenta un mejor desempeño.
La convergencia del modelo explícito fue estudiada analítica y numéricamente, se encontró una expresión analítica (Ec. (25)) que da el valor del paso de tiempo máximo para la región de convergencia. Este máximo está asegurado para el primer paso de tiempo y es suficiente para el suelo de tipo arenoso analizado, sin embargo para el suelo compuesto este análisis no es suficiente para asegurar estabilidad, pues el valor cambia y es función del tiempo de simulación. Por ese motivo, debe analizarse numéricamente el valor efectivo de paso de tiempo máximo. No se ha encontrado una forma de identificar a priori si un suelo corresponde al primer o segundo caso.
Finalmente, se puede decir que los tres modelos convergen a la misma solución por el análisis de sensibilidad para la variable ?t y el modelo de Crank-Nicolson presenta los menores errores relativos en la zona del frente húmedo que a pesar de su mayor complejidad, requiere un tiempo de cómputo reducido.

Referencias

1. Castañeda McCormick, M. C.; Reyes Anaya, H. A. Solución Numérica a la Ecuación de Richards, 2004.         [ Links ]

2. Wulfsohn, D.; Adams, B.A. and Fredlund, D.G. Application of unsaturated soil mechanics for agricultural conditions. Canadian Agricultural Engineering, 38(3): 173-181, 1996.         [ Links ]

3. Martinez, J. L.; Schvezov C. E. y Rosenberger M. R. Aproximación en diferencias finitas a la ecuación de Richards para transporte de agua en suelos no saturados. Mecánica Computacional, Vol. XXXII, págs. 2779-2793, 2013.         [ Links ]

4. Genuchten, M.T. Van. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892-8, 1980.         [ Links ]

5. Wendland, E. e Pizarro, M. Modelagem Computacional do fluxo unidimensional de águaemmeionão saturado do solo. Eng. Agríc., 30:424-434, 2010.         [ Links ]

6. Celia, M.; Bouloutas, E. and Zarba R. A general mass-conservative numerical solution for the unsaturated flow equation. Water resources research, 26:1483-1496, 1990.         [ Links ]

7. Fredlund, D.G. and Xing, A. Equations for the soil-water characteristic curve. Canadian Geotechnical Journal, 31(3): 521-532. 1994.         [ Links ]

8. Szymkiewicz, A.; Helmig, R. Comparison of conductivity averaging methods for one-dimensional unsaturated flow in layered soils. Advances in Water Resources, 34(8), 1012-1025, 2011.         [ Links ]

9. Chapra S., Canale. Métodos numéricos para ingenieros, México, Mc Graw Hill, pp. 896., 2006.         [ Links ]

Recibido: 20/11/2014.
Aprobado: 24/02/2015.