ARTICULOS

Critical phenomena in the spreading of opinion consensus and disagreement

 

A. Chacoma,¹ D. H. Zanette¹'²*

* E-mail: zanette@cab.cnea.gov.ar

¹ Instituto Balseiro and Centro Atómico Bariloche, 8400 San Carlos de Bariloche, Rio Negro, Argentina.
² Consejo Nacional de Investigaciones Científicas y Tecnicas, Argentina.

---

Received: 11 March 2014, Accepted: 1 August 2014
Edited by: G. Martinez Mekler fr^xCi, Reviewed by: F. Bagnoli, Dipartimento di Fisica ed Astronomia, Università degli Studi di Firenze, Italy

Licence: Creative Commons Attribution
3.0 DOI: http://dx.doi.org/10.4279/PIP.060003 _ ISSN 1852-4249

---

 

We consider a class of models of opinion formation where the dissemination of individual opinions occurs through the spreading of local consensus and disagreement. We study the emergence of full collective consensus or maximal disagreement in one- and two-dimensional arrays. In both cases, the probability of reaching full consensus exhibits well-defined scaling properties as a function of the system size. Two-dimensional systems, in particular, possess nontrivial exponents and critical points. The dynamical rules of our models, which emphasize the interaction between small groups of agents, should be considered as complementary to the imitation mechanisms of traditional opinion dynamics.

I. Introduction

The remarkable regularities observed in many human social phenomena -which, in spite of the disparate behavior of individual human beings, emerge as a consequence of their interactions- have since long attracted the attention of physicists and applied mathematicians. Collective manifestations of human behavior have been mathematically modeled in a variety of socioeconomic processes, such as opinion formation, decision making, resource allocation, cultural and linguistic evolution, among many others, often using the tools provided by statistical physics [1]. The stylized nature of these models emphasizes the identification of the generic mechanisms at work in human interactions, as well as the detection of broadly significant features in their macroscopic outcomes. They provide the key to a deep insight into the common elements that underlie those processes.

Models of opinion formation constitute a central paradigm in the mathematical description of social processes from the viewpoint of statistical physics. Starting in the seventies and eighties [2-5], much work -which we cannot aim at inventorying here, but which has been comprehensibly reviewed in recent literature [1]- has exploited the formal resemblance between opinion spreading and spin dynamics in order to apply well-developed statistical techniques to the analysis of such models.

The key mechanism driving most agent-based models of opinion formation is imitation. For instance, in the voter model -to which we refer several times in the present paper- the basic interaction event consists in an agent copying the opinion of another agent chosen at random from a specified neighborhood. At any given time, the opinion of each agent adopts one of two values, typically denoted as ±1. The voter model can be exactly solved for populations of agents distributed over regular (hyper)cubic arrays in any dimension [6]. For infinitely large populations, it is characterized by the conservation of the average opinion. In one dimension, a finite population always reaches an absorbing state of full collective consensus, all agents sharing the same opinion. The probability of final consensus on either opinion coincides with the initial fraction of agents with that opinion, and the time needed to reach the absorbing state is of the order of the population size squared [1].

In this paper, we present an introductory analysis of a class of models where opinion dynamics is driven by the spreading of consensus and disagreement, rather than by the dissemination of individual opinions. The basic concept behind these models is that agreement of individual opinions in a localized portion of the population may promote the emergence of consensus in the neighborhood while, in contrast, local disagreement may inhibit the growth of, or even decrease, the degree of consensus in the surrounding region. In real social systems, the mechanism of consensus and disagreement spreading should be complementary to the direct transmission of opinions between individual agents. In our models, however, we disregard the latter to focus on the dynamical effects of the former.

Since the degree of consensus can only be defined for two or more agents, the spreading of consensus and disagreement engages groups of agents rather than individuals. Such groups are, thus, the elementary entities involved in the social interactions [7-11]. We stress that several other social phenomena - related, notably, to decision making [10] and resource allocation [12]- are also based on group interactions that cannot be reduced to two-agent events. In the class of models analyzed here, each interaction event is conceived to occur between two groups: an active group G and a reference group G'. As a result of the interaction, the agents in G change their individual opinions in such a way that the level of consensus in G approaches that of G'. This generic mechanism extends dynamical rules where the opinion of each single agent changes in response to the collective state of a reference group [1,8,13,14]. The size and internal structure of the interacting groups, as well as the precise way in which opinions are modified in the active group with respect to the reference group, defines each model in this class. For the sake of concrete-ness, we limit the analysis to systems where, as in the voter model, individual opinions can adopt two values (±1). In the next section, we analyze the case where both the active group and the reference group are formed by two agents, and the population is structured as a one-dimensional array. In this case, the system admits stationary absorbing states of full consensus and maximal disagreement, with simple scaling laws with the population size. In Section III., we study a two-dimensional version of the same kind of model with larger groups, where nontrivial critical phenomena -not present in the one-dimensional case- emerge. Results and perspectives are summarized in the final section.

II. Two-agent groups on one-dimensional arrays

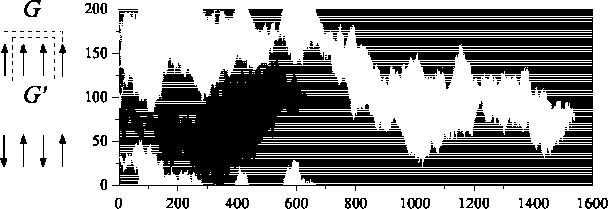
We begin by considering the simple situation where each of the two groups involved in each interaction event is formed by just two agents. The situation within each group, thus, is one of either full consensus (when the two agents bear the same opinion, either +1 or -1) or full disagreement (when their opinions are different). We take a population where agents are distributed on a one-dimensional array, and consecutively labeled from 1 to N. Periodic boundary conditions are applied at the ends. At each time step, we choose four contiguous agents, say, i - 1 to i + 2. The central pair i, i + 1 acts as the reference group G^'. If they are in disagreement, the agents i -1 and i+2 respectively adopt the opinions opposite to those of i and i +1 with probability p_D, while with the complementary probability 1 - p_D nothing happens. If, on the other hand, i and i + 1 agree with each other, i - 1 and i + 2 copy the common opinion in G' with probability p_c, while with probability 1 - p_c nothing happens. In this way, both consensus and disagreement spread from G^' outwards, to the left and right. The probabilities pc and p_D control the relative frequency with which consensus and disagreement are effectively transmitted. The left panel of Fig. 1 illustrates the states of the four consecutive agents in the two possible outcomes of the interaction (up to opinion inversions).

time
Figure 1: Left: The two possible outcomes of the interaction, up to opinion inversions, for four consecutive agents along the one-dimensional array. The active and the reference groups, G and G^', are respectively formed by the outermost and innermost agents. Right: Time evolution of a 200-agent array with n+(0) = 0.5 and p_D = p_c = 1. Black and white dots correspond, respectively, to opinions +1 and -1. At time t = 1534, an absorbing state of maximal disagreement is reached.

 

It is not difficult to realize that, for p_D = p_c = 1, our one-dimensional array is equivalent to two intercalated subpopulations -respectively occupying even and odd sites- each of them evolving according to the voter model. The dynamical rules are reduced in this case to binary interactions between agents. In fact, whatever the opinions in group G^' at each interaction event, agent i - 1 and i + 2 respectively copy the opinions of i +1 and i. Now, since the voter model always leads a finite population to an absorbing state of full consensus, the final state of our system can be one of full consensus on either opinion, or a state of maximal disagreement where opposite opinions alternate over the sites of the one-dimensional array. In the latter, the two neighbors of each agent with opinion +1 have opinion - 1 and vice versa. The right panel of Fig. 1 shows the evolution of a 200-agent array for n+(0) = 0.5 and p_D = p_c = 1, black and white dots respectively corresponding to opinions +1 and - 1. At any given time, the population is divided into well-defined domains either of consensus in one of the opinions or disagreement. Note that the domain boundaries show the typical diffusive motion found in stochastic coarsening processes [1,15].

Taking into account that, in the voter model, the probability of ending with full consensus on opinion +1 is given by the initial fraction of agents with that opinion, n+(0), and assuming that the initial distribution of opinions is homogeneous over the array, the probability that our system ends in a state of full consensus on either opinion is P_cons = n+(0) + n-(0) = 1 - 2n+(0) + 2n+(0). Note that this coincides with the probability that, in the initial state, any two contiguous agents are in consensus. Moreover, we know that the time needed to reach an absorbing state in the one-dimensional voter model is proportional to N², a result that should also hold in our case.

The upper panel of Fig. 2 shows numerical results for the probability of final full consensus P_cons, determined as the fraction of realizations that ended in full consensus out of 10³ runs, as a function of n+(0) and for several population sizes N. The curve is the analytic prediction given above. The result is analogous to the probability of final consensus found in Sznajd-type models [13]. The lower panel shows the total time T needed to reach the final absorbing state (of either consensus or disagreement), averaged over 10³ realizations and normalized by N². As expected, both P_cons and N^-2T are independent of the population size.

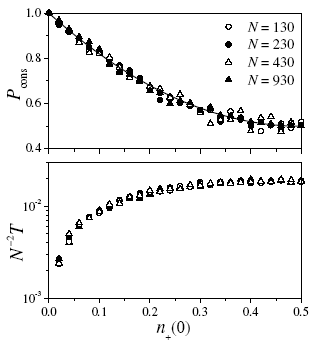
Figure 2: Numerical results for consensus and disagreement spreading on a one-dimensional array with p_D = p_c = 1, obtained from 10³ realizations for each parameter set (see text for details). Upper panel: Probability of reaching full consensus, P_cons, as a function of the initial fraction of agents with opinion +1, n+ (0), for four values of the population size N. Lower panel: Total time T needed to reach the final absorbing state, normalized by the squared population size N². Since both P_cons and N^-2T are symmetric with respect to n+(0) = 1/2, only the lower half of the horizontal axis is shown.

When p_D p_c, the two intercalated subpopulations cannot be considered independent of each other any more. If p_D < p_c, for instance, an opinion prevailing in one of the subpopulations will invade the other subpopulation faster than the opposite opinion, thus favoring the establishment of collective consensus. To analyze this asymmetric situation, we first fix p_c = 1 and let p_D vary in (0,1), so that the spreading of consensus is more probable than that of disagreement. The main plot in Fig. 3 shows numerical results for P_cons, measured as explained above, as a function of p_D and for four values of N. In all the realizations, n+(0) = 0.5, and the two opinions are homogeneously distributed over the population. As p_D decreases below 1, the probability of reaching full consensus grows rapidly, approaching P_cons = 1. As N grows, moreover, the change in P_cons is more abrupt. Fitting of a sigmoidal function to the data of P_cons vs. p_D near p_D = 1 makes it possible to assign a width to the range where P_cons changes between 1 and 0. 5. The insert of Fig. 3 shows this width as a function of the system size N in a log-log plot. The slope of the linear fitting is -1.00 ± 0.02.

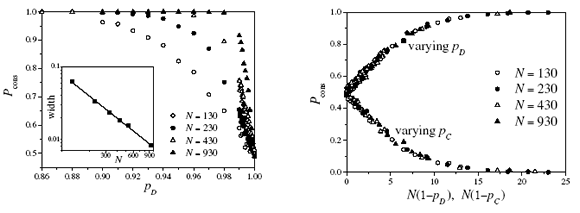
Figure 3: Probability of reaching full consensus, P_cons, as a function of the probability p_D, with pc = 1 and for four values of the system size N. Results were obtained averaging over 10³ realizations for each parameter set. Insert: Width of the variation range of P_cons as a function of N. The straight line has slope - 1.
Figure 4: Probability of reaching full consensus, ^Pcons^{, as a} function of N(1 — p_D) when varying p_D with pc = 1, and as a function of N(1 — pc) when varying p_c with p_D = 1.

 

Therefore, the width is inversely proportional to N.

Analogous results were obtained when fixing p_D = 1 and p_c was varied. Now, P_cons drops to 0 in a narrow interval for p_c just below 1, indicating the prevalence of disagreement. Again, the width of the interval is proportional to N^-1. The results in the lower half of Fig. 4 ("varying pc ") illustrate the collapse of the corresponding values of P_cons when plotted against N(1 - p_c).

In our numerical realizations with p_D = p_c, we have also recorded the average time T needed to reach the final absorbing state. Figure 5 shows results for N^-2T in the case where p_c = 1 and p_D changes (cf. lower panel of Fig. 2). In contrast with the case with p_D = p_c = 1, rescaling of the time T with N² leaves a remnant discrepancy between results for different population sizes N. Specifically, for p_D < 1, T grows faster than N². Moreover, T is nonmonotonic as a function of p_D, exhibiting a minimum which shifts towards p_D = 1 as N grows. The same dependence with N and p_c is observed when we fix p_D = 1 and let p_c vary.

Figure 5: Total time T needed to reach the final absorbing state, normalized by the squared population size N², as a function of the probability p_D (pc = 1). Bezier curves have been plotted as a guide to the eye.

Summarizing our results for a one-dimensional population with two-agent groups, we can say that the possibility that both consensus and disagreement spread over the system makes it possible to find absorbing collective states of either full consensus, with all the agents having the same opinion, or maximal disagreement, where opposite opinions alternate between consecutive neighbor agents. For large populations, the relative prevalence of collective consensus and disagreement is controlled by how the probabilities p_D and p_c compare with each other. Our results suggest that, in the limit N - oo, the condition p_c > p_D univocally leads to full consensus and vice versa. For smaller sizes, however, the system can approach full consensus even when p_D > p_c, and vice versa -presumably due to finite-size fluctuations.

III. Larger groups on two-dimensional arrays

A two-dimensional version of the above model, where agents occupy the N = L x L sites of a regular square lattice with periodic boundary conditions, can be defined as follows. The reference group G' at each interaction event is a randomly chosen 2 x 2-agent block. The corresponding active group G is formed by the eight nearest neighbors to the agents in G which are not in turn members of the reference group. The active group, thus, surrounds G'. Of the sixteen possible opinion configurations of the reference group, two correspond to full consensus -with the four agents sharing the same opinion- and six correspond to maximal disagreement -with two agents in each opinion. The remaining eight configurations correspond to partial consensus, with only one agent disagreeing with the other three. The dynamical rules are the following: (1) if G' is in full consensus, all the agents in G copy the common opinion in G'; (2) if G' is in maximal disagreement, each agent in G adopts the opinion opposite to that of the nearest neighbor in G'; (3) otherwise, nothing happens. Hence, both consensus and disagreement spread outwards from the reference group. Probabilities p_D and p_C for the spreading of disagreement and consensus are introduced exactly as above. The left part of Fig. 6 shows, up to rotations and opinion inversions, the three possible outcomes of a single interaction event.

The states of full collective consensus -with all the agents in the population having the same opinion- and of maximal collective disagreement -with the two opinions alternating site by site along each direction over the lattice- are absorbing states, in correspondence with the one-dimensional case. However, for p_D = p_C = 1, the system cannot be reduced anymore to a collection of sublattices governed by the voter model. The definition of G and G' establish now correlations between the opinion changes in the active group at each interaction event. Moreover, some opinion configurations in the reference group induce evolution in the active group, while others do not. Figure 6 shows, to its right, four snapshots of a 120 x 120-agent population, along a realization starting with n+(0) = 0.35 and p_D = p_C = 1. Note the formation of consensus clusters at rather early stages, and the final prevalence of disagreement. The line boundaries between disagreement regions are also worth noticing.

Following the same lines as for the one-dimensional array, we study first the probability Pcons of reaching full collective consensus as a function of the initial fraction of agents with opinion +1, n+(0), in the case p_D = p_c = 1. Opinions are homogeneously distributed all over the population. For very small n+(0), as expected, we find P_cons ~ 1. However, in sharp contrast with the one-dimensional case (see Fig. 3), P_cons remains close to its maximal value until n+(0) « 0.35, where it drops abruptly to P_cons ~ 0. The width of the transition zone decreases as a nontrivial power of the system size, ~ l°'^{83±0 04}, as illustrated in the insert of Fig. 7. Our best estimate for the critical value of n+(0) at which P_cons drops is n+^rit = 0.353 ± 0.001. The main plot in the figure shows the collapse of numerical measurements of Pcons as a function of n+(0) for different sizes L, averaged over 100 realizations, when plotted against the rescaled shifted variable L°'⁸³[n₊(0) - 0.353].

Figure 6: Left: The three possible outcomes of the interaction, up to ±90° rotations and opinion inversions, on the two-dimensional lattice. The active and the reference groups, G and G^', are respectively formed by the outermost and innermost agents. Right: Four snapshots of a population with L = 120, for n+(0) = 0.35 and p_D = p_c = 1, including the initial condition and two intermediate states. At time t = 3207, an absorbing state of maximal disagreement has been reached. Black and white dots correspond, respectively, to opinions +1 and 1.

These results suggest that, for very large populations, the probability of reaching full consensus jumps discontinuously from P_cons = 1 to 0 at n+(0) = n+^rit. Compare this with the smooth, size-independent behavior of the one-dimensional case. Note also that n+^rit is close to, but does not coincide with, n+(0) = 1/3. At this latter value, in the initial condition with homogeneously distributed opinions, the probability of finding a 2 x 2-agent block in full consensus becomes lower than that of maximal disagreement as n+(0) grows.

 

Figure 7: Numerical results for the probability of reaching full consensus, P_cons, on a two-dimensional lattice with p_D = p_c = 1, obtained from 100 realizations for each parameter set. Collapse for several system sizes L is obtained plotting P_cons against L^0.83[n₊(0) - 0.353]. Insert: Scaling of the width of the transition zone of P_cons, determined from fitting a sigmoidal function, as a function of the size L. The straight line has slope -0.83.

In the above simulations, we have also measured the average total time T needed to reach the final absorbing state. Results are shown in Fig. 8. Again in contrast with the one-dimensional case, T exhibits a remarkable change in its scaling with the system size as n+(0) overcomes the critical value n+^rit.

Going now to the dependence of P_cons on the probability of disagreement spreading p_D -with p_c = 1 and n+(0) = 0.5- it qualitatively mirrors that of the one-dimensional case, shown in Fig. 3. Namely, as p_D decreases from 1, P_cons grows from 0 to 1 in an interval whose width decreases with the population size. In the two-dimensional system, however, the transition takes place at a critical probability that can be clearly discerned from p_D = 1. Our estimate is = 0.984 ± 0.002. Moreover, the scaling of the transition width with the population size exhibits a nontrivial exponent, decreasing as . Collapse of the rescaled numerical results for various sizes, obtained from averages of 100 realizations, are shown in Fig. 9, where we plot P_cons as a function of L^0.93(0.984 - p_D) (cf. Fig. 4). The insert displays the power-law dependence of the width on the size L. Analogous results are obtained if the probability of consensus spreading pc is varied, with p_D = 1.

Figure 8: Total time T needed to reach the final absorbing state in a two-dimensional lattice, as a function of n+(0), for different sizes L.

Finally, we have found that the transition in P_cons as a function of the disagreement probability pD shows a dependence on the initial fraction of agents with opinion +1. To characterize this effect in a way that highlights the relative prevalence of disagreement and consensus, we have measured the value of p_D at which the probability of getting full collective consensus reaches Pcons = 0.5, as a function of n+(0). The parameter plane (n+(0),p_D), thus, becomes divided into regions where a final state of full consensus is more probable than that of maximal disagreement, and vice versa. Results for a 120 x 120-agent population are presented in Fig. 10.

In summary, while spreading of consensus and disagreement on a two-dimensional lattice bears superficial qualitative similarity with the one-dimensional case, the probability that the population reaches full collective consensus in two dimensions exhibits a quite different dependence on the system size, on the initial conditions, and on the spreading probabilities. In particular, our results reveal the existence of critical phenomena involving scaling laws with nontrivial exponents.

Figure 9: Collapse of numerical results for the probability of reaching full consensus, P_cons, on a two-dimensional lattice with p_c = 1 and n+(0) = 0.5, for several system sizes L when plotted against L^{0 93}(0.984 - p_D). Insert: Scaling of the width of the transition zone of P_cons as a function of the size L. The straight line has slope -0.93.

Figure 10: Zones of relative prevalence of full consensus and maximal disagreement in a two-dimensional lattice with L = 120, plotted on the parameter plane (n+(0),p_D). Symbols stand for numerical results, and the curve serves as a guide to the eye.

 

IV. Conclusion

In this paper, we have considered the emergence of collective opinion in a population of interacting agents where, instead of imitation between individual agents, opinions are transmitted through the spreading of local consensus and disagreement toward their neighborhoods. The basic interacting units in this mechanism are not individual agents but rather small groups of agents which mutually compare their internal degrees of consensus and modify their opinions accordingly. In this sense, it extends the basic mechanism underlying such models as the majority-rule and Sznajd-like dynamics [1,8,13], where the opinion of each individual agent changes in response to the collective state of a reference group. It is expected that in real social systems the dissemination of individual opinions through agent-to-agent imitation on one side, and the spreading of consensus and disagreement by group interaction on the other, are complementary mechanisms simultaneously shaping the overall opinion distribution. Here, in order to gain insight on the specific effects of the second class, we have focused on models solely driven by the spreading of consensus and disagreement. The combined effects of the two mechanisms is a problem open to future work.

Our numerical simulations concentrated on two-opinion models evolving on one- and two-dimensional arrays [14]. In both cases, absorbing states with all the population bearing the same opinion (full consensus) and with half of the population in each opinion (maximal disagreement) are possible final states for the system. Maximal disagreement states are characterized by alternating opinions between neighbor sites along the arrays.

A relevant quantity to characterize the behavior is the probability of reaching full consensus, as a function of the initial condition -i.e., the initial fraction of the population with each opinion- and of the relative probabilities of consensus and disagreement spreading. The total time needed to reach the final absorbing state, averaged over realizations, has also been measured as a characterization of the dynamics. We have found that, in several cases, these quantities display critical phenomena when the control parameters are changed, with power-law scaling laws as functions of the system size, pointing to the presence of discontinuities in the limit of infinitely large populations. It is interesting to remark that the scaling laws are rather simple for one-dimensional arrays, but involve nontrivial exponents and critical points in the case of two-dimensional systems.

Within the same one- and two-dimensional models analyzed here, an aspect that deserves further exploration is the dynamics and mutual interaction of the opinion domains that develop since the first stages of evolution (Figs. 1 and 6). However, the most interesting extension of the present analysis should progress along the direction of considering more complex social structures. The interplay between the dynamical rules of consensus and disagreement spreading and the topology of the interaction pattern underlying the population might bring about the emergence of new kinds of collective self-organization phenomena.

Acknowledgements - We acknowledge enlightening discussions with Eduardo Jagla. Financial support from ANPCyT (PICT2011-545) and SECTyP UNCuyo (Project 06/C403), Argentina, is gratefully acknowledged.

 

1. C Castellano, S Fortunato, V Loreto, Statistical physics of social dynamics, Rev. Mod. Phys. 81, 591 (2009).

2. W Weidlich, The statistical description of polarization phenomena in society, Br. J. Math. Stat. Psychol. 24, 251 (1971).

3. R Holley, T Liggett, Ergodic theorems for weakly interacting infinite systems and the voter model, Ann. Probab. 3, 643 (1975).

4. S Galam, Y Gefen, Y Shapir, A mean behavior model for the process ofstrike, J. Math. Sociol. 9, 1 (1982).

5. S Galam, Majority rule, hierarchical structures and democratic totalitarism: A statistical approach, J. Math. Psychol. 30, 426 (1986).

6. S Redner, A guide to first-passage processes, Cambridge University Press, Cambridge (2001).

7. K Starkey, Ch Barnatt, S Tempest, Beyond networks and hierarchies: Latent organization in the UK television industry, Org. Sci. 11, 299 (2000).

8. P Krapivsky, S Redner, Dynamics of majority rule in two-state interacting spin systems, Phys. Rev. Lett. 90, 238701 (2003).

9. J Johnson, Multidimensional events in multilevel systems, In: The Dynamics of Complex Urban Systems, Eds. S Albeverio et al., Pag. 311, Physica-Verlag, Heidelberg (2008).

10. D H Zanette, Beyond networks: Opinion formation in triplet-based populations, Phil. Trans. R. Soc. A 367, 3311 (2009).

11. D H Zanette, A note on the consensus time of mean-field majority-rule dynamics, Pap. Phys. 1, 010002 (2009).

12. D G Hernandez, D H Zanette, Evolutionary dynamics ofresource allocation in the Colonel Blotto game, J. Stat. Phys. 151, 623 (2013).

13. K Sznajd-Weron, J Sznajd, Opinion evolution in closed community, Int. J. Mod. Phys. C 11, 1157 (2000).

14. D Stauffer, A O Sousa, S M de Oliveira, Generalization to square lattice of Sznajd socio-physics model, Int. J. Mod. Phys. C 11, 1239 (2000).

15. A Bray, Theory of phase-ordering kinetics, Adv. Phys. 43, 357 (1994).