INGENIERÍA - TECNOLOGÍA

Aumento de la Velocidad de Convergencia del Sistema de Rachford-Rice

Improvement of The Rachford-Rice System Convergence Rate

 

Omar A. Iglesias¹, Estanislao J. Petryla²

¹– Facultad de Ingeniería, Universidad Nacional de La Plata, 1 y 48, La Plata.
²– Facultad de Ciencias Exactas, Químicas y Naturales, Universidad Nacional de Misiones, Félix de Azara 1552, Posadas. petryla@fceqyn.unam.edu.ar.

• Omar Alfredo Iglesias¹ Ingeniero Químico, Becario Iniciación y Perfeccionamiento en la Investigación del CONICET. Profesor Titular Ordinario con Dedicación Exclusiva, Facultad de Ingeniería, UNLP, Director de proyecto de Investigación.
• Estanislao Juan Petryla² Ingeniero Químico, Magíster en Ingeniería, Profesor Titular, dedicación exclusiva, FCEQyN, Universidad Nacional de Misiones. Director de varios proyectos de Investigación relacionados con la Optimización.

 

---

Resumen

El método de Regula-Falsi para resolver la ecuación f (x) = 0 resulta adecuado cuando en las dos iteraciones iniciales la función presenta distinto signo. En tal caso es posible estructurar un proceso de búsqueda de la raíz de la función de modo que la velocidad de convergencia esté asegurada, aun en los casos en los cuales dicha convergencia, debido a la característica de la función involucrada, fuera sumamente lenta. Funciones cuyas velocidades de convergencia son muy lentas se presentan, por ejemplo, en la separación de algunos componentes utilizando destilación flash en condiciones adiabáticas. Desde el punto de vista matemático, el problema consiste en encontrar la temperatura y el grado de vaporización a partir de las ecuaciones de Rachford-Rice. En este trabajo, presentamos un método que asegura buena velocidad de convergencia, aun para aquellos casos en que, normalmente, dicha velocidad fuera prohibitivamente lenta.

Palabras Clave: Regula-Falsi; Convergencia; Flash adiabático; Optimización.

Abstract

The Regula-Falsi method to solve the equation f (x) = 0 is very adecuate when in the two first iterates x₀ and x₁, f (x) have opposite signs. Howewer, in some cases, the convergence of this method can be very slow, specially when i) the images through f of the extreme points of the search interval differ, at least, in one order of magnitude; ii) in the zone where f (x) is smaller, f (x) ≈ 0 and iii) the root of f (x) is approximately in the mean of the search interval. For this cases, in this paper we propose a convergence accelerator function, wich is then used to calculate a adiabatic flash, where are present the characterisitcs of f mentioned above.

Key Words: Regula-Falsi; Convergence; Adiabatic flash; Optimization.

---

 

Introducción

Para la búsqueda de raíces de ecuaciones no lineales en una variable real, existen dos tipos de métodos: de convergencia por intervalos y puntual. Los métodos de convergencia por intervalos parten de un intervalo que acota la raíz y, en cambio, los puntuales parten de una estimación inicial de la raíz y tratan de aproximarse a ella. Para los primeros la convergencia está garantizada aunque suelen ser más lentos; para los segundos, la convergencia no está garantizada, aunque son más rápidos cuando la búsqueda se realiza en las cercanías de la raíz. Los métodos de convergencia por intervalos se basan en el teorema de Bolzano, que garantiza para toda función continua en un intervalo en el que cambia de signo, (o sea f (x)∈C⁰ en [a, b], con f (a) f (b)<0 ), que existe al menos una raíz ξ∈ (a, b) de f (x) = 0. El método de Regula–Falsi (1)se basa en el Teorema de Bolzano; caracteriza la recta que corresponde a una interpolación lineal de la función entre los puntos (a, f (a)) y (b, f (b)) y realiza la búsqueda de su raíz. Dicha raíz es el punto que se toma como próxima iteración. El algoritmo que se utiliza tiene los siguientes pasos:

1– Encontrar un intervalo [a, b] tal que f (a) f (b)<0 sea a = x₀.

2– Caracterizar la función de la línea recta que une los puntos (a, f (a)) y (b, f (b)):

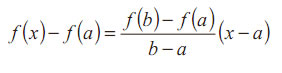
3– Encontrar la raíz de f (x):

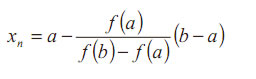
4– Si f (x_n) = 0, hemos terminado.

5– Si f (a) f (x_n)>0 y f (b) f (x_n)<0, elegir como intervalo [x_n, b].

6– Si f (b) f (x_n)>0 y f (a) f (x_n)<0, elegir como intervalo [a, x_n].

7– Condición de parada: si |x_n - x_n-1|>ε entonces repetir el paso (3). En otro caso, terminar tomando a x_n como raíz del problema, con un error acotado por ε.

Si bien el algoritmo tiene convergencia superlineal, existen casos para los cuales la velocidad de convergencia es prohibitivamente lenta. Como ejemplo, puede citarse las funciones f (x) = exp (-2x)-0,1, para x∈ (0,3) y f (x) = x¹⁰-1, con x∈ (0, 1,25), donde, para cualquiera de ellos, para conseguir que |f(x)|<10^-6 o |x_k+1-x_k|<10^-6 se requieren más de cuarenta pasos.

Para ambos casos se cumplen las siguientes características:

i) Las funciones, evaluadas en los extremos de los intervalos de búsqueda, difieren en un orden de magnitud.

ii) La derivada en la zona de menor valor está próxima a cero.

iii) La raíz se encuentra en un valor medio del intervalo.

En Ingeniería química, funciones similares se presentan en la separación de algunos componentes utilizando destilación flash en condiciones adiabáticas. Desde el punto de vista matemático, el problema consiste en encontrar la temperatura y el grado de vaporización a partir de las ecuaciones de Rachford–Rice (2–4), optimizando la velocidad de convergencia (5).

Si bien se encuentran métodos diseñados para mejorar el comportamiento del algoritmo (6, 7), ninguno de ellos plantea el diseño de una función aceleradora como la que se propone en este trabajo, que tiene la ventaja de ser simple, eficaz y aplicable para todos los casos que reúnan las condiciones planteadas en los ejemplos. Asegura buena velocidad de convergencia aun para aquellos casos en que, normalmente, dicha velocidad fuera muy lenta.

Caracterización del Método

El proceso iterativo de Regula–Falsi, cuando se considera a x₀ fijo, se reduce a:

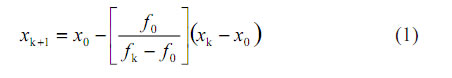
Si se supone que |f₀|>>|f₁|, (f₁ = -|α|f₀, |α|<<1) y que en las proximidades de x1, f_k≈f₁ + f'₁(x_k - x₁), con f'₁≈0, se puede poner (1) como:

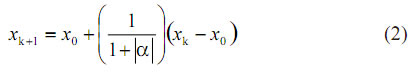
y, por lo tanto:

 

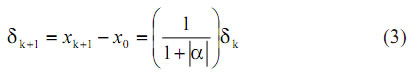
y puede verse que el proceso iterativo {x₀, x₁....} comenzará en las proximidades de x₁ y se irá moviendo muy lentamente hacia la raíz, ya que el factor entre paréntesis es levemente inferior a la unidad.

Si consideramos otra función g(x) que, en el intervalo [x₀, x₁] tiene las mismas raíces que f (x), pero donde g(x₁)≈- g(x₀), puede acelerarse el proceso de convergencia. En efecto, si: g(x) = (c₀ + c₁x)f (x) = h(x)f (x) con:

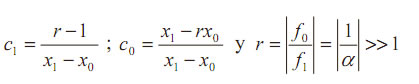
entonces: i) Es fácil probar que g(x₁) -g(x₀). En efecto:

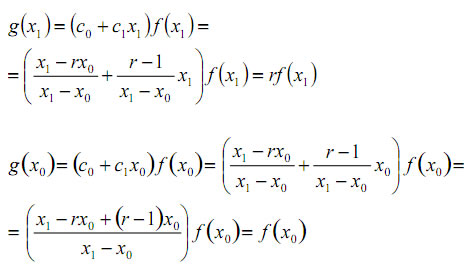
A partir del valor de r y del hecho de que f (x₀)f(x₁)<0, queda probado de que g(x₀) = -g(x₁). ii) La función g(x) = (c₀ + c₁x)f (x), en el intervalo [x₀, x₁], tiene las mismas raíces que f (x). En efecto, la raíz de la función c₀ + c₁x es:

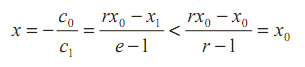
y, por ende, g(x) se anula cuando lo hace f (x) en el mencionado intervalo. Introduciendo la función h(x) la relación (1) queda:

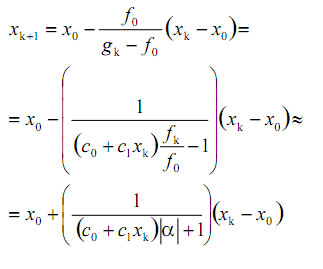
y, por lo tanto:

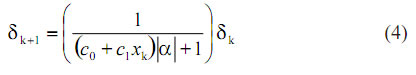
Comparemos las expresiones (4) y (3). La función h(x_k)=c₀ + c₁x_ktransforma elementos del intervalo [x₀ , x₁ ] en elementos de [1, r]. En efecto:

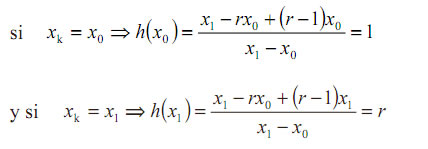
Teniendo en cuenta, además, la linealidad de h(x_k), queda probada la afirmación anterior. Analicemos ahora el comportamiento del factor:

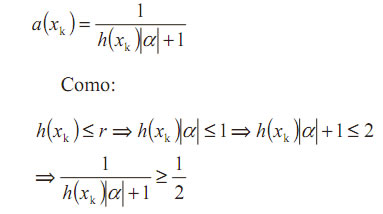
y, por otra parte:

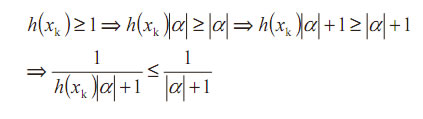
Por lo tanto:

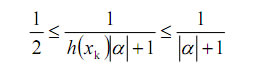
Por hipótesis, la raíz de f (x) está, aproximadamente, en el valor medio del intervalo [x₀, x₁]. Si suponemos que dicho valor está exactamente en el medio entonces la sucesión estará acotada por el valor:

Entonces, cuando k = 1 en la sucesión , a(x_k) = ½ y, a medida que k crece, a(x_k)→⅔ con lo que queda probado que la inclusión de la función h(x_k) acelera notablemente la convergencia del método, bajo las hipótesis enunciadas¹.

Aplicación del Método propuesto al cálculo de un "Flash" adiabático

Uno de los procesos de separación más difundidos a nivel industrial es la destilación, ya que permite obtener productos de elevada pureza y recuperar sustancias que pueden ser reincorporadas al proceso. Uno de los casos es la destilación flash, la que consta de una sola etapa de equilibrio. El estudio de esta operación en particular es de interés, debido a que una columna de destilación completa puede considerarse como una sucesión de cámaras de flash adiabáticas. Se trata de un problema en el que no se agrega ni se extrae calor de un tanque como el que aparece en la Figura 1.

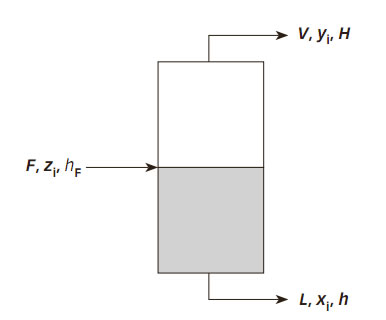
Figura 1. Tanque "Flash" adiabático.

El balance de calor a presión constante es:

donde Q es la cantidad de calor agregada por unidad de tiempo. Si hacemos qf = Q/F, entonces la ecuación (6) se puede poner de la forma:

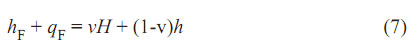
Por otra parte, a partir de las relaciones:

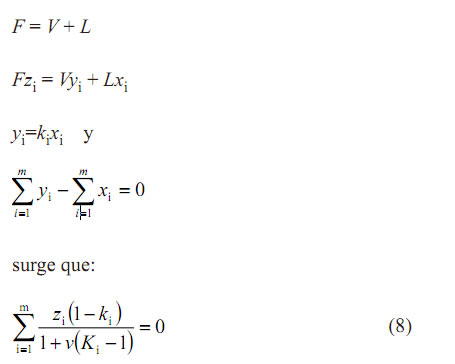
Desde el punto de vista matemático el problema consiste en encontrar la temperatura y el grado de vaporización que satisfagan las ecuaciones (7) y (8) a la presión y entalpías dadas. En otras palabras, habrá que resolver el sistema no lineal que sigue:

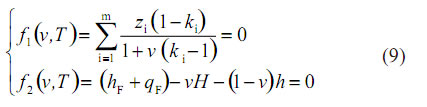
Para resolver el sistema, tenemos como datos P, h_f+ q_f y {Z_i } y tendremos que suponer T₀, {x_i} e {y_i }. El proceso de resolución se puede efectuar de acuerdo al algoritmo que aparece en la Figura 2.

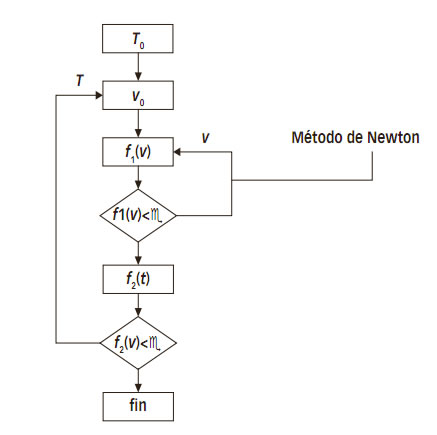
Figura 2. Diagrama de solución de un sistema para el "Flash" adiabático.

El lazo interior se puede resolver utilizando el método de convergencia de Newton, ya que es factible calcular la derivada de f₁sin dificultades; con ello se asegura una convergencia de primer orden. En el lazo externo, como no se puede evaluar la derivada de f ₂ en forma explícita, es necesario recurrir a un método que no la requiera, por ejemplo el Regula–Falsi. Por las características de f ₂, la convergencia puede ser muy lenta, por lo que es conveniente utilizar un acelerador de convergencia del tipo que se ha presentado. Aplicándolo, tendremos el siguiente proceso iterativo:

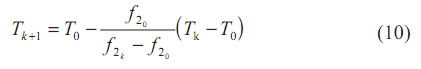
Tomemos:

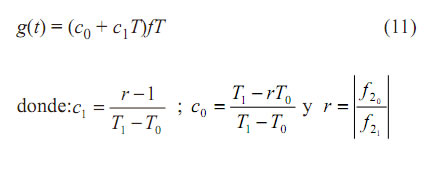
Con ello, (10) queda:

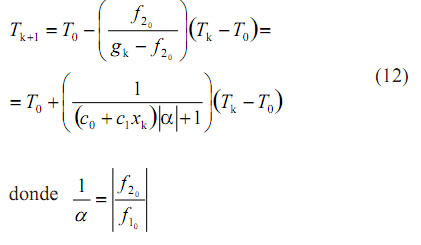
Aplicaremos las relaciones halladas en el siguiente caso²: utilizando un flash adiabático, se procesa una corriente de seis hidrocarburos que se dan más abajo. La entalpía de la alimentación es 13210 Btu y la presión es de 300 psia. La composición de la alimentación y los valores de k son:

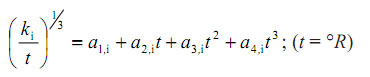
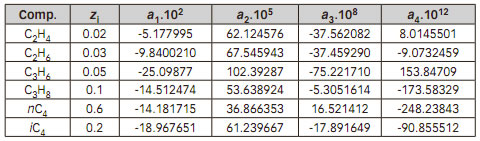
Entalpía (T en °R)

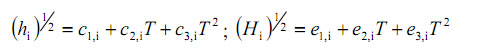
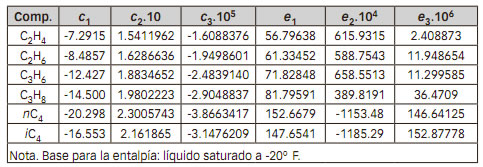
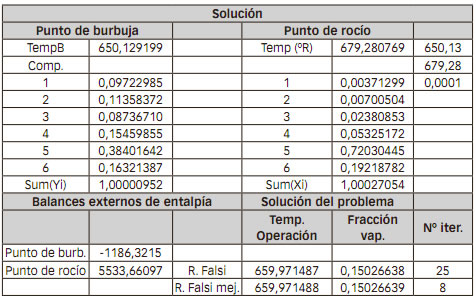
Resultados y Discusión

Bajo las hipótesis enunciadas, esta función aceleradora produce un aumento considerable de la velocidad de convergencia (alrededor del 30 % para el caso del ejemplo). Por consiguiente, resulta ventajosa su utilización, especialmente en aquellos casos donde la derivada de la función en aquel extremo donde toma menor valor, es casi nula. Es necesario remarcar que el método propuesto se ha diseñado pensando en problemas específicos de Ingeniería Química, en los cuales no es posible utilizar el método de Newton; si se pudiera utilizar un algoritmo Newton, seguramente su velocidad será superior al método propuesto. Finalmente, la función aceleradora propuesta tiene como una ventaja adicional: su implementación no trae dificultades matemáticas de ningún tipo.

Notas

1– Queda evidente que la convergencia se desacelera cuanto más cerca se encuentre la raíz de x0.
2– Este ejemplo está tomado de (3); las unidades no han sido transformadas al sistema internacional (SI) debido a que nuestro interés está en conocer el número de iteraciones necesarias para llegar a la solución del problema más que su solución.

Bibliografía

1. Ledanois, J.; López, A.; Pimentel, J. A.; Pironti Lubran, F. F. Métodos Numéricos Aplicados a la Ingeniería; McGraw–Hill, 2000.         [ Links ]

2. Edgar, T. F.; Himmeblau, D. M. Optimization of Chemical Processes. Mc–Graw–Hill Inc. 1988.         [ Links ]

3. Henley, E. J.; Seader J. D. (1999), Equilibrium–Stage Separation Operations in Chemical Engineering, Wiley, John&Sons, 1981.         [ Links ]

4. King, C. J. Separation Processes, McGraw–Hill Book Co, 1981         [ Links ]

5. Nocedal, J.; Wright, S. J. Numerical Optimization, Springer, 1999.         [ Links ]

6. Wu, X. Y.; Shen, Z. H.; Xia, J. L. An improved regula falsi method with quadratic convergence of both diameter and point pr enclosing simple zeros of nonlinear equations, Appl. Math. Comput, 144 (2003), pp. 381–388.         [ Links ]

7. Chen, J. H.; Li, W. G. An exponential regula falsi method for solving nonlinear equations, Numer. Alg. 41 (2006), pp. 327–338.         [ Links ]

Recibido: 25/10/07.
Aprobado: 07/10/08.