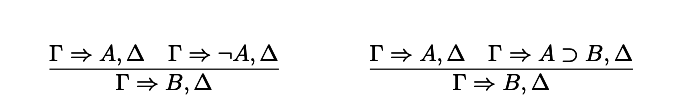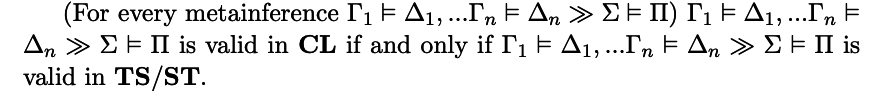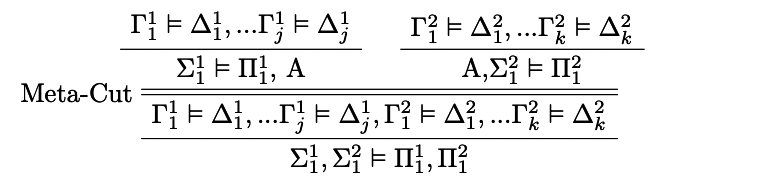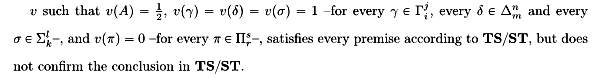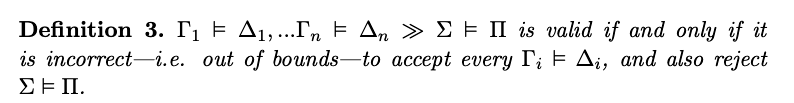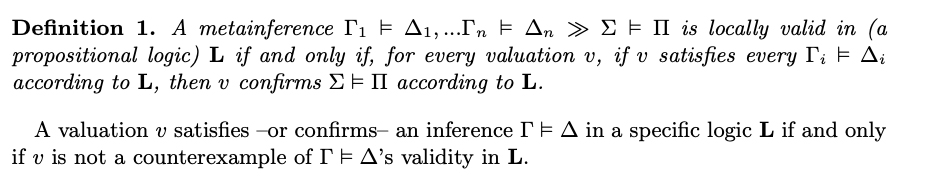1. Introduction

According to a widespread point of view, logic is about what follows from what. Logical systems are an abstract explanation of this connection. Classical logic is a theory (maybe a true theory) about this relation. Other non-classical logics (as paraconsistent systems) give up some classical features of the relation of logical consequence (for example, it might no longer be true that everything follows from a contradiction). Perhaps these logics and classical logic are rivals. Or maybe they are just complementary systems: the context might provide the right answer as to which system is the appropriate one. Maybe classical logic might be recaptured in some non-classical systems. ¹ Sometimes the differences between different logics are directly connected with the properties of the notion of logical consequence. Substructural logics focus on what happens with the notion of consequence in the absence of structural rules, e.g., properties that do not depend on any logical vocabulary. Not all structural properties are related to premise combination. Reflexivity, Contraction, Weakening and, Cut are the ones that have received most of the attention. ²

The main idea that we want to defend in this paper is that the question of what is a logic should be addressed differently when structural properties enter the game. In particular, we want to support the idea that it is not enough to identify a logic with its set of valid inferences. In other words, we will argue that two logical theories could identify the same set of validities (e.g. its logical truths and valid inferences), but fail to be the same logic. This means that although structural rules may not affect the set of validities, they play an essential role in fixing the set of valid inferences between inferences —usually called metainferences. We will offer a new characterization of what a logic is that takes these aspects into consideration. According to our position, this will allow us to give a better characterization of what classical logic is. We will try to answer to the following question: How should a logic be characterized when the structural properties are considered? Specifically, we will try to illuminate the problems related to what it takes for a logic to be classical, when is a logic non-classical —and, in particular, when a logic is paraconsistent. ³

These issues constitute one of the central points of Uncut, Dave Ripley’s book, and probably the most important defense of a non-transitive logic. Roughly, Ripley is a semantic inferentialist. He supports a bilateralist view that connects the notion of validity with the normative status of sets of assertions and denials. He also seems to implicitly adopt the usual extensional conception according to which a logic can be identified with the set of its validities. From this, he concludes that the calculus CFOLE (a sequent calculus for classical logic without Cut as a basic rule), is classical logic CL. So, according to Ripley,

I’ll show later in the chapter that ⊢_{C L} is exactly CFOLE, but the claim should not be surprising: all the above rules encode familiar classical behaviour for the bits of vocabulary involved. (Ripley, ²⁰¹⁸, p. 59)

However, we are going to present some reasons to reject the identification between the calculus CFOLE and CL. Our main point will be to show that when one is interested in substructural properties, logics cannot be identified only with their set of validities.

The paper is structured as follows. In the next section, we present what we consider to be a misleading view about what a logic is. According to this—more traditional—view, a logic is characterized through its set of valid inferences. This view seems to be supported by Dave Ripley, and that seems to be why he thinks that CFOLE is just CL in disguise. We will present a series of arguments against this approach, and argue for the view according to which a logic is better characterized through its valid inferences and metainferences. Finally, in Section 3, we provide some concluding remarks.

2. A Misleading View about what a Logic is

Over the last years, the agreement that classical logic cannot be used for capturing transparent truth in self-referential situations has been challenged by Ripley. Roughly, the main idea is to take a standard sequent calculus for plain old classical logic without Cut as a basic rule, and extend it with rules for a transparent truth predicate. The Cut rule is admissible in the logical fragment of the calculus, but yet it fails to be so once the truth rules are added. ⁴ It is exactly this failure of Cut that saves truth from paradoxes, when we attempt to reproduce a derivation of the Liar (or any other paradox, see, for example Barrio, Rosenblatt & Tajer, ²⁰¹⁵). Nevertheless, Ripley argues that CFOLE is classical logic CL. According to Ripley (²⁰¹⁸, p. 50),

I believe CL is rule-correct for ^⊩. Readers who were already suspicious of classical logic, however, almost certainly retain their suspicion at this point. While I’ve rehearsed familiar stories about this vocabulary, I haven’t said anything particularly original to persuade someone who was not already tempted by these stories. Nonetheless, I’ll move forward with CL as it stands; some choice is necessary here, and this is not a book primarily about the logical vocabulary at all.

The extensionality thesis according to which two different logics are the same logic if and only if their systems identify the same set of validities is implicit in the following quote: “the idea, as ever, is that CL is correct (that is, that Γ ⊢ A only if Γ ^⊩ A) because it is rule-correct (that is, that each rule of CL preserves ^⊩ validity).”

Nevertheless, we do think that some conclusions regarding a calculus can be extended to its semantic consequence relation. And, especially, in the case of CFOLE, which is also sound and complete concerning the semantic consequence relation ST. Using such elements, we are going to argue that ST—and therefore, CFOLE— is not classical logic. In particular, we will defend the idea that logics—and CL in particular—cannot be identified only with their set of validities. This means, ultimately (though we would not pursue a defense of this thesis here) that it is not a good idea to give an extensional criterion of what is a logic—and in particular, this is not the correct way to characterize classical logic. It is not enough for two logics to identify the same set of validities to be the same logic.

Recently, Barrio, Rosenblatt, and Tajer (²⁰¹⁵) and Barrio, Pailos, and Szmuc (²⁰¹⁸) draw attention to certain paraconsistent aspects of ST (and consequently, of CFOLE). Both papers have shown that —through some suitable translation— the set of valid inferences in LP coincides with the set of valid meta-inferences in ST. First among these is Cut. Despite being admissible in CFOLE, a sequent calculus sound and complete concerning ST does not have Cut as a basic rule, Cut is not locally valid in ST. ⁵ Nevertheless, it is valid in the traditional two-valued semantics for CL. Moreover, metainferential schemes closely related to Modus Ponens, Modus Tollens and Explosion turn out to be valid in CL, but invalid in ST. Two relevant examples are the following—that we will call Meta-Explosion and Meta-Modus-Ponens.

As it is pointed out in Barrio, Rosenblatt, and Tajer (2015), all these metainferences are invalid LP inferences (under a suitable translation). Therefore, only if one passes over all these metainferential facts, ST, and consequently CFOLE, could be identified with CL. However, if one considers that failures of Cut and other related matainferencial schemes cannot be ignored, then one has good reasons to reject the standard view according to which a logic is only its set of validities.

In our view, facts linked to failures of some metainferences could be considered constitutive of what a logic is. After all, a logic without Cut, or without the metainferential schemes closely related to Modus Ponens, Modus Tollens and Explosion seems far from being classical.

To stress our point, we will briefly introduce a new propositional logic, called TSST. TSST is a consequence relation for metainferences, and not just for inferences. ⁶

TSST is particularly interesting because of the following result (proven in Pailos, ²⁰²⁰ and Barrio, Pailos, & Szmuc, ^2020a):

Nevertheless, TS/ST is not fully classical. Many classically valid meta- metainferences –e.g., metainferences of level 2– are invalid in TSST. In particular, the meta-metainference that we will call Meta − Cut, turns out to be invalid in TSST.

It is not hard to explain why Meta − Cut is invalid in TSST. Take any instance of it that involves only propositional letters, where A is different from every other sentence in the premises and the conclusion. The valuation:

It should be noticed that two logics can fully coincide in its sets of metainferences while failing to be the same. That is, the action happens not only at the level of the metainferences. Two logics can share all their metainferences, while not being the same logic. In particular, CL and TSST have the same metainferences, but differ in the set of meta-metainferences. In particular, not every classically valid meta-metainference is valid in TSST. ⁷

Finally, according to us, Ripley’s stance is not compatible with the distinction between theories with a single policy about the validity of a specific rule—in the broader sense in which, e.g., Explosion and Meta-Explosion are the same rules —and those that have a combined policy about those rules— for example, because they admit Explosion while rejecting Meta-Explosion, or the other way around. We claim that this difference is relevant when identifying logic.

At this point, it is necessary to reconsider the relation between CL and TSST. These calculi not only have the same valid inferences, but also the same valid metainference (of level 1). As we have already mentioned, it is odd to think of them as the same logic. Specifically, there will be classically valid meta-metainferences that are not valid in TSST. Nevertheless, both if one thinks that a logic should be characterized through its inferences—as Ripley seems to think— these two systems identity the same logic.

If we aim to discriminate between them, it is not enough to consider that both levels –e.g., the inferential and the metainferential– are relevant. So, if every metainferential level counts, then they are indeed very different logics.

Thus, every inferential level counts if we are in the business of (extensionally) characterizing a logic. But it is possible to make these criteria a bit more precise. Traditionally, a logic was supposed to be defined by its tautologies —e.g., the formulas satisfied by every model. But a formula could not only be a tautology, but a logical falsehood —e.g., a formula that no model satisfies— or a contingency —e.g., a formula satisfied by some model, but not by all of them. If a logic is defined not only by its valid formulas, but also by the logical falsehoods and contingencies that it determines, then it is not necessary to move from the inferential level to distinguish extensionally between CL and LP. For example, A ∧ ¬A will be a CL’s logical falsehood, but an LP contingency. Moreover, depending on how we define the notion of contingency and logical falsehood in ST, then A ∧ ¬A will be an ST contingency too. Thus, we may even distinguish CL and ST without moving to the inferential or the metainferential level. This, of course, is not what the traditional ST supporter wants.

Before ending, we want to address here two worries. The first one is the following: Ripley himself seems not to be very interested in the question of whether CFOLE is or is not CL. “Although I will assume CL for the full vocabulary in play, you might think that my failure to impose cut means that what I’m up to here is not really classical. Whatevs, I don’t think it’s clear at all what it would take to be ‘really classical’; there are too many distinct distinctions in the area” (Ripley, ²⁰¹⁸, p. 60).

And he adds:

Consider normal modal logics, of the sort studied in Blackburn et al. (2001). These are often counted as nonclassical in Ono (1998); Priest (2008a), but seemingly just as often counted as classical in Williamson (2013). Or consider the debate about whether supervaluationist logics are classical. This is not a debate about which clearly-defined properties supervaluationist logics do or don’t have; all the relevant questions have clear answers. It is a question about what it takes to be classical. Field (2008) uses the notions ‘weakly classical’ and ‘strongly classical’, in an attempt to bring some clarity to the situation, and the distinction has been picked up in Scharp (2013); Schechter (2011). But a two-way division will not suffice, although it is useful for some purposes; there are more than just two notions floating around in the area. (Ripley, ²⁰¹⁸, p. 60)

This seems to be a substantial philosophical disagreement between Ripley and us. Of course, the important question is not so much whether a logic is classical or paraconsistent, but the criterion on the basis of which we can identify a logic. The same logic can be introduced using different semantic tools, or through distinct proof-systems. The systems obtained are just different presentations of the same logic. Thus, the relevant question here is whether CFOLE, ST, LP and CL are the same logic. For us, this amounts to asking which are the valid inferences (as Ripley holds), but also which are the valid metainferences. Moreover, there is one kind of paraconsistency involved in the metainferential relationship between CFOLE and ST—e.g., there is a specific metainferential form of Explosion that we have called Meta-Explosion that is invalid in both of them—that does not allow us to identify these logics with CL. Moreover, even if one adopted an inferentialist view, each inferential level should be important to analyze a system of logic.

The second worry we want to address was posed to us by an anonymous referee, and is the following. One reason why we might content ourselves with only going up the second level, i.e., the first metainferential level, is that this, as Restall argues, has a straightforward interpretation in terms of positions consisting of assertions (the antecedent) and denials (the consequent). Nevertheless, this does not appear to be the case with the higher levels.

As one of the referees pointed out, a kind of bilateral interpretation for them is available, but it will be distinctively ‘second (or third, or...) order’. So while the first metainferential level has a natural interpretation, those above it will be genuinely ‘meta’.

Nevertheless, the bilateralist reading is not that straightforward. For example, an incorrect bilateralist reading of local metainferential validity is the following:

If accepting a (meta)inference of level n − 1 is equivalent to accepting that it is valid, this will not give a reading of local validity. If this were the case, this criterion could be paraphrased like this: a metainference is valid if and only if, if each premise is valid, so is the conclusion. Moreover, this seems to be a reasonable candidate to interpret global metainferential validity. But this is not what we are looking for.

A better way to read local metainferential validity in a bilateralist fashion is as follows:

To claim that maintaining this pair of attitudes that we have mentioned is incorrect, is equivalent to quantifying over possible attitudes, where each attitude could be plausibly represented by a valuation. But this reading does not run out of problems. The main one of which seems to be that it does not look at all like a bilateralist interpretation, because it only appeals to one attitude: rejection—and its negation. Despite what it looks like, it gives us what we were looking for. We should understand the attitude of not rejection as primitive, and non-reducible to rejection. We could call it weak acceptance. Thus understood, the bilateralist reading would look like this:

Here, to weakly accept something should be understood as equivalent to considering and not discarding it. When can a (meta) inference be discarded? When is it invalid? This reading, as we said before, is bilateralist because it explains metainferential validity regarding two mutually irreducible attitudes: rejection and weak acceptance. ⁸

One last clarification: we are not subscribing to a bilateralist reading of local metainferential validity. We only affirm that this reading is available for those who endorse a bilateralist approach to validity in general. ⁹

Thus, we agree both in that bilateralist interpretation’s of metainferences is distinctively second (or third, or...) order, and, therefore (as the referee seems to suggest) it is not as natural as the bilateralist interpretation for sequents, or inferences. While we think this is true, we also believe that it is not bilateralist interpretation’s fault, but of metainferences themselves. People make inferences all the time. Nevertheless, they rarely engage in metainferential reasoning. That is why the bilateralist reading of metainferences seems not that natural. Any interpretation of metainferences will sound a little bit unnatural. But this is just because metainferences themselves are rare creatures.

3. Conclusion

In sum, we have defended the idea that to characterize a logic, not only the inferential level, but also every metainferential level is necessary. Thus, if one considers that CL is a paradigmatic case of a classical logic, then no logic that shares CL’s vocabulary, but is different from it at the inferential or any metainferential level, can be considered as truly classical. Moreover, even if we stick to the level of formula, it is possible to distinguish between logics that have the same tautologies by assessing whether they share the contingencies and logical falsehoods.