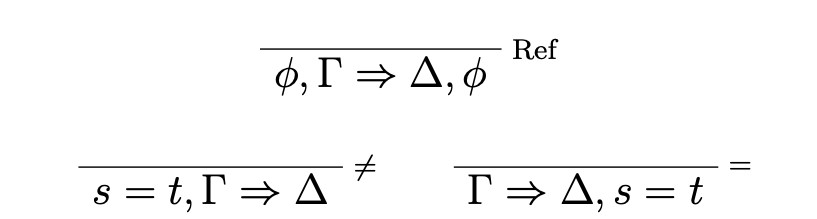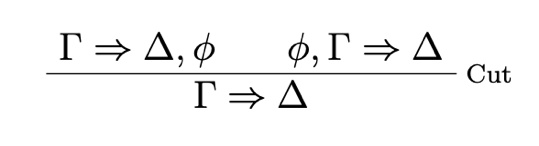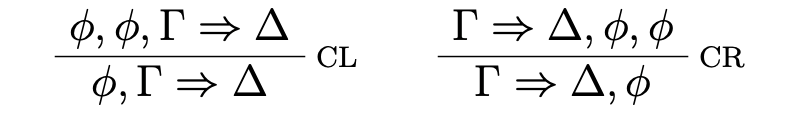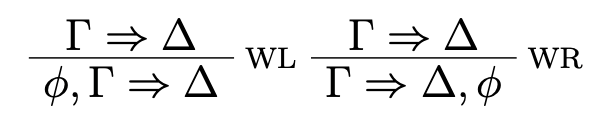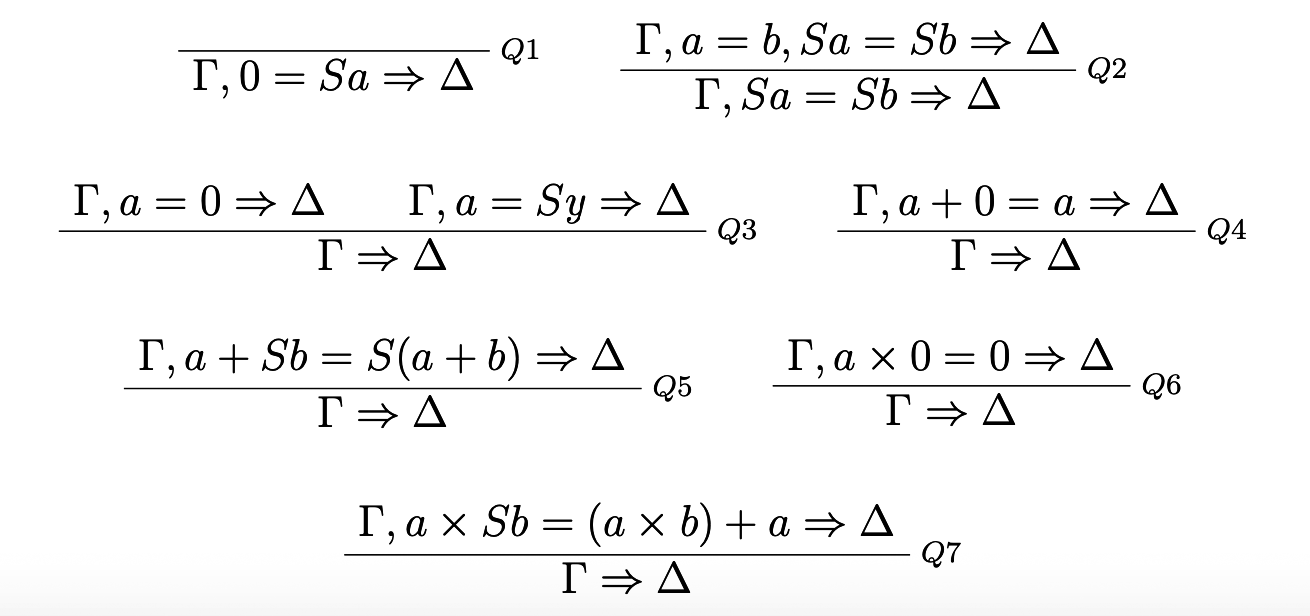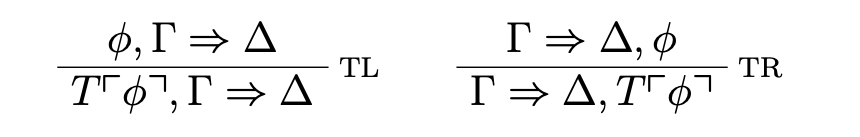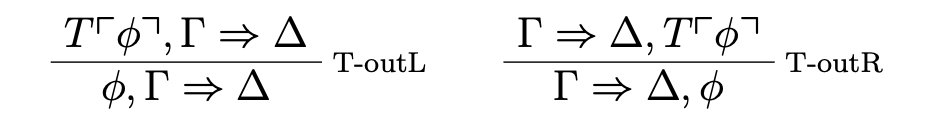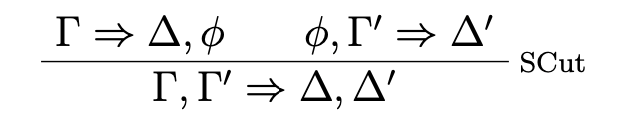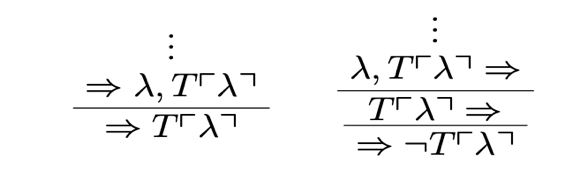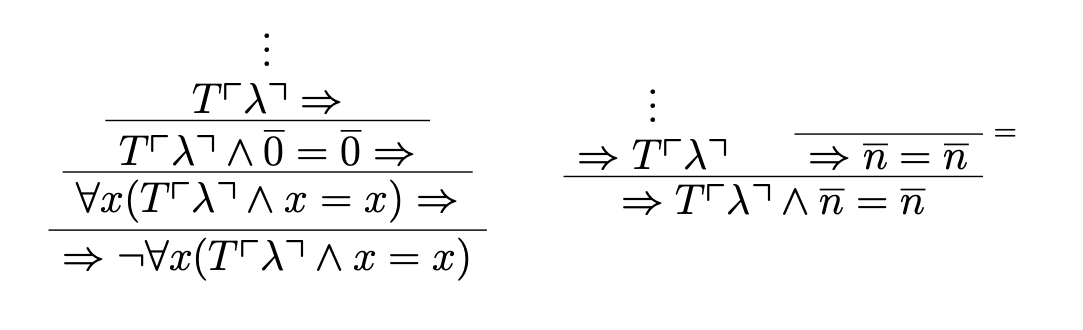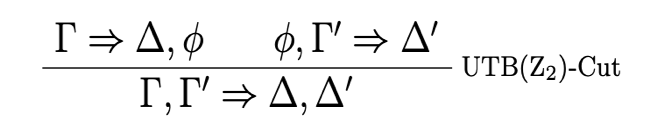Truth, Cut and PA

David Ripley argued extensively for a nontransitive theory of truth by dropping the rule of Cut in a sequent calculus setting in order to get around triviality caused by paradoxes such as the Liar. He has made advancements in this direction in a more model-theoretic fashion (Ripley, ²⁰¹²) as well as more proof-theoretically (Ripley, ^2013a). His upcoming book Uncut (Ripley, ²⁰¹⁸) will surely give a great overview over the research that went into nontransitive and other substructural theories of truth and their motivations. Here we want to advance the project of a nontransitive theory of truth by proposing a restriction of Cut, which allows for proof-theoretically very strong non-transitive theories over the arithmetical theory of Peano Arithmetic (PA).

In comparison to substructural theories of truth, classical theories have been around a lot longer and are often more technically advanced and well understood. Especially with classical theories of truth it is standard to study truth-theoretical principles with a background of arithmetical axioms, typically those of PA. Authors engaging in this work cite a couple of reasons for doing so (see e.g. Halbach, ²⁰¹¹), but here we are not concerned with these reasons. If one is not convinced by these (or other) reasons or likes to think of the nontransitive approach as going in a different direction, the following observations about a nontransitive theory of truth over PA might still be interesting due to a technical curiosity and the possibility to compare the nontransitive approach with a long and established line of papers in the literature.

Independently of the chosen background theory, the truth predicate T is seen as a predicate applying to terms t, among which are names of sentences. One benefit of using a suitably strong arithmetical background theory is that it can handle the coding necessary to refer to sentences via codes. We work in the language of first-order arithmetic containing the zero-constant ¯0 , a symbol for the successor function S, as well as for basic arithmetical operations x, + with the standard interpretation and of course our truth-predicate T. The standard inductive definition for wffs applies. We then fix a standard Gödel-coding (see e.g. Smith (²⁰¹²)) and write #ϕ for the Gödel-code of ϕ and ⌜ϕ⌝ for the numeral of the Gödel-code of ϕ. Where n is a natural number, we denote its numeral by ¯n .

A primitive recursive substitution function s is represented by its function symbol s.. Where ϕ is a formula with only x free, s.(⌜ϕ⌝, t) is to be read as the numeral of the code of the result of replacing every occurrence of x in ϕ by t. The dot notation such as s.(⌜ϕ⌝, t) is an abbreviation for ⌜ϕt⌝. This allows us to quantify into predicate position, into e.g. the truth predicate with e.g. ∀xT ⌜ϕx. ⌝.

We work in a sequent calculus environment. Where Γ and Δ are sets of formulae of L, Γ⇒Δ is a sequent. Ripley’s nontransitive logic ST (for strict-tolerant) with some minor modifications to fit in identity is given by the following sequent rules:

given in ≠ that s = t does not hold and given in = that s = t holds.

As always, y in the right ∀-rule must be an eigenvariable. Crucially, the rule of Cut

is not included in STT.

The structural rules of Contraction

are trivially admissible in the system, since sequents are defined using sets rather than multisets. The structural rules of Weakening are admissible as well (see e.g. Negri, von Plato & Ranta, ²⁰⁰¹, p. 75).

We are now interested in formulating the theory of PA over our nontransitive logic ST. In order to guarantee that the resulting theory proves the same sequents as when formulating PA over fully structural classical logic, it must be the case that Cut is in principle eliminable. We begin with Robinson Arithmetic (Q), i.e. PA without Induction. (von Plato, ²⁰¹⁴) has shown that there is a formulation of the axioms of Q as sequent-rules, s.t. Cut in the resulting theory is eliminable (given a suitable formulation of the logical rules as e.g. given above):

Where y in Q3 must be an eigenvariable. So there is no inherent problem of formulating Q over ST in terms of the sequents being provable ¹ . However, things change as we proceed to full PA by adding Induction as a rule:

The result of adding the rules Q¹ — Q⁶ and Induction to ST is called STA (for strict-tolerant arithmetic). It is easy to show that STA does not prove the same sequents as PA, since Cut is not eliminable in the latter theory (Troelstra & Schwichtenberg, ²⁰⁰⁰). Since our nontransitive theory lacks Cut, there are sequents of PA, which it does not prove. We take it that this is not acceptable for a theory of truth based on an arithmetical background theory. Although some rule needs to be restricted in order to block the paradoxes, a theory of truth should at least preserve all things provable in the background theory.

Thus what we need is a restriction of the Cut rule, s.t. at least all sequents of PA are provable but adding suitable rules for T does not result in triviality. A straightforward restriction would be to simply allow Cut iff the Cut-formula is arithmetical, i.e. does not include T. This would block the above problem and ensure that STA proves the same sequents as PA. Consider this option for the moment.

We finally extend our nontransitive arithmetical theory to a theory of truth STAT (for strict-tolerant arithmetical truth) by adding the following T-rules:

Although STAT proves all sequents of PA, it can also easily be shown that it is conservative over PA:

Lemma 1.1. Let ϕ∈Γ∪Δ be arithmetical. If ⊢_STAT Γ ⇒ Δ, then ⊢_PA Γ ⇒ Δ.

Proof. Assume for contradiction that there is an arithmetical sequent Γ ⇒ Δ s.t. STAT proves it, but PA does not. Then there must at least one application of TL or TR in the proof. However, STAT has no elimination rules for T and Cut is restricted to arithmetical formulae. Thus the introduced truth-predicate cannot be eliminated, contradicting the fact that Γ ⇒ Δ contains only arithmetical formulae. ◻

Proof. Assume for contradiction that there is an arithmetical sequent Γ ⇒ Δ s.t. STAT proves it, but PA does not. Then there must at least one application of TL or TR in the proof. However, STAT has no elimination rules for T and Cut is restricted to arithmetical formulae. Thus the introduced truth-predicate cannot be eliminated, contradicting the fact that Γ ⇒ Δ contains only arithmetical formulae. ◻

It might be objected that this argument can be blocked by adding elimination rules for T (as Ripley often does):

But this does not strengthen the system as the rules are admissible in STAT:

Lemma 1.2. T-outL and T-outR are admissible in STAT.

Proof. The proof is by Induction on the height of the proof. If T ⌜ϕ⌝, Γ ⇒ Δ is an initial sequent, we distinguish the following cases. If Γ ⇒ Δ is an initial sequent as well, so is ϕ, Γ ⇒ Δ. If it is not, then T ⌜ϕ⌝ must be in Δ. We first obtain ϕ, Γ ⇒ Δ’, ϕ (where Δ’=Δ–{T ⌜ϕ⌝}) and then apply TR on ϕ to obtain ϕ, Γ ⇒ Δ. The same strategy goes through for T-outR. For the induction step, we distinguish the cases of T ⌜ϕ⌝ being principal or not. If it is principal, the conclusion is immediate. If it is not, simply apply the Induction hypothesis to (one of) the previous line(s). ◻

The conservativity of STAT over PA also means that it is much weaker than many popular classical theories of truth like KF. In order to strengthen our nontransitive theory, we need a looser restriction on Cut, which also allows for some applications if the Cut-formula includes the truth predicate.

Restricting Cut

Consider a classical, disquotational axiomatic theory of truth S. An axiomatic theory of truth is said to be disquotational, if its only axioms concerning T are instances of the (uniform) T-schema ϕ ↔ T ⌜ϕ⌝. Since S is classical, it has an unrestricted Cut-rule (given a suitable formulation in a sequent calculus) in the sense that it includes the Cut rule for all formulae ϕ ∈ L. However, in order for it to be consistent, it must lack some instances of the (uniform) T-schema. So in a sense its Cut rule (and all its other rules) is restricted compared to the naive theory of truth. The classical theory does not contain any application of Cut, s.t. the Cut-formula was derived using an instance of the T-schema, which is not included in S. By eliminating some instances of the T-schema, we also eliminate those Cuts which could have been applied after making use of those instances of the T-schema. This is not a restriction in terms of the language but a proof-theoretic restriction with respect to the history of how the premises of a rule are derived.

This approach follows a remark by Ripley, which has (as far as I know) never been worked out in detail:

This suggests adding a restricted rule of cut to the target systems. Such a rule could be used in a derivation only above truth (...) rules, never below them. That is, the premises of the cut would have to be derived without use of the truth (...) rules, although any rules at all could be freely applied to the conclusion of the cut. (Ripley, ^2013b, p. 11)

To see why this observation might be fruitful in blocking the paradoxes, let us take a look at a derivation of the empty sequent via the Liar paradox. Obtain a typical liar sentence λ via diagonalisation s.t. ⇒ λ ↔ ¬T ⌜λ⌝ is provable. By the invertibility of our rules for the conditional and negation (Negri et al., ²⁰⁰¹), it holds that the system proves the sequents λ, T ⌜λ⌝⇒ and ⇒ λ, T ⌜λ⌝. The empty sequent can now be derived as follows:

The derivation up to the sequents λ, T ⌜λ⌝⇒ and ⇒λ, T ⌜λ⌝ can be obtained in PAT, i.e. PA formulated in the language including the truth predicate. This means that up to this point, the derivation does not involve any truth-theoretic principles like T-rules or instances of the (uniform) T-schema. After applying TL and TR, we only need to apply Cut in order to derive the empty sequent. We will soon show that this holds for every derivation of the empty sequent or triviality.

Exploiting this fact we can construct a restricted rule of Cut relative to some classical, axiomatic theory of truth S as follows: Cut is only applicable if its premises were derived using only rules of S. This way we can extract the Cut-rule of S by considering only those applications, which could have happened within S itself.

So given S, our nontransitive theory STAT[S] is obtained by closing S under TL and TR and replacing its Cut rule by

given that the derivations leading to the Cut-premises only contain rules of S (where S is of course the original classical theory before the closure under TL and TR). We read STAT[S] as ‘strict-tolerant arithmetical truth over S’. Since any classical theory of truth contains PA, STAT[S] will prove all sequents of PA as well.

Before considering some particular instances of S, we show some basic lemmata about the non-triviality of the resulting systems:

Lemma 2.1. Let S be a classical, consistent theory of truth. Then STAT[S] does not prove the empty sequent.

Proof. Assume for contradiction that STAT[S] proves the empty sequent. Since S is consistent and closed under Cut, the derivation concluding the empty sequent must involve an application of a T-rule not included in S. But the only rule which could eliminate the principal formula of this rule would be Cut, which is restricted to formulae derived using only rules of S. So there can be no derivation of the empty sequent. ◻

This lemma is of course not enough to ensure that STAT[S] is non-trivial, since the theory is not closed under Cut.

Lemma 2.2. Let S be a classical, consistent theory of truth. Then STAT[S] is non-trivial.

Proof. Assume for contradiction that STAT[S] is trivial. Pick some arithmetical formula ϕ, s.t. S by itself does not derive ⇒ϕ. So the derivation of ⇒ϕ must include an application of a T-rule not included in S. However, the principal formula of this T-inference cannot occur in the conclusion sequent for the conclusion is arithmetical. But the only rule which could eliminate the principal formula of this T-inference would be Cut, which is blocked since the derivation must include a T-inference not included in S. ◻

Despite its nontriviality, our nontransitive theory is both inconsistent and (therefore) ω-inconsistent:

Lemma 2.3. STAT[S] is inconsistent and ω-inconsistent

Proof. The inconsistency can easily be shown by recreating the proof of the Liar above:

The ω-inconsistency can then easily be derived as follows. Consider the formula T ⌜λ⌝ ∧ y = y. We can then show that STAT[S] proves ¬∀x (T ⌜λ⌝ ∧ x = x) and T ⌜λ⌝ ∧ ¯n = ¯n for every n ∈ ω:

Now in order to show how we can easily construct very strong nontransitive theories of truth, consider the strongest disquotational theory of truth known. (Schindler, ²⁰¹⁸; Picollo & Schindler, ²⁰¹⁸) define the axiomatic theory of truth UTB(Z₂) as PAT plus all instances of the uniform T-schema ∀x1,...,xn (T ⌜ϕ(x1,...,xn)⌝↔ϕ(x1,...,xn)), where ϕ is a translation of a formula of second-order Arithmetic into our first-order language containing T (the details of translation do not matter here) and the quantifiers of the T-schema are restricted to translated formulae.

We can then construct our nontransitive theory STAT[UTB(Z₂)] as follows. First, we need to give a suitable translation of UTB(Z₂) (which is typically given as a Hilbert-style calculus) into a sequent calculus. To do so, simply consider the theory of naive truth NT, i.e. extending STAT by an unrestricted Cut-rule. A sequent calculus for UTB(Z₂) is then obtained by admitting formulae (not just sentences) as active formulae of TL and TR and restricting these rules to translated formulae of second-order arithmetic. It can easily be shown that the theory derives all instances of the uniform T-schema if formulae with free variables are allowed as active formulae of TL and TR.

Our desired nontransitive theory of truth can then be constructed as follows. We start with UTB(Z2) and close it under those instances of TL and TR which it lacks. This means adding all instances of TL and TR s.t. the active formulae are not translated formulae from the language of second-order arithmetic. Finally, we replace its Cut rule by

which is only applicable given that the derivations leading up to the Cut-premises only contain rules of UTB(Z₂). Here we only formulate the restriction of Cut by a criterion of the metalanguage. However, it is easy to express this property via an indexed sequent calculus. One can introduce different indices, which is changed whenever a T-inference not contained in S is used. The Cut-rule is then restricted with respect to this index in a straightforward way.

It is easy to see that S is always a proper subtheory of STAT[S] and so the latter proves everything the former does. Since UTB(Z₂) is very strong, this makes STAT[UTB(Z₂)] very strong as well. Some already very strong theories of truth have a proof-theoretic ordinal of ϵ₀ or even Γ₀ . But UTB(Z₂) goes well beyond that: These theories are proof-theoretically weaker than the subsystem of second-order arithmetic with Π ₁ ¹-comprehension. But UTB(Z₂) relatively interprets any subsystem with Π _n ¹-comprehension for any n ∈ ω! This illustrates that we can easily construct very, very strong nontransitive theories of truth. In fact, the theory is so strong that there currently is not even a notation to capture its proof-theoretic ordinal. The things just said also hold for a somewhat weaker theory of truth, namely UTB(Z _₂ ) introduced in Schindler (²⁰¹⁵).

Halbach and Nicolai (²⁰¹⁸) and Halbach and Horsten (²⁰⁰⁶) have argued repeatedly in favour of classical over non-classical approaches by pointing out that non-classical approaches are very bad in trying to recapture arithmetical theorems. The problem is typically that even if the non-classical theory recaptures the classical rules for arithmetical formulae, one cannot make use of truth-theoretic principles in order to prove new arithmetical theorems such as Con(PA). Halbach and Horsten (²⁰⁰⁶) have shown this as a weakness of a gappy axiomatisation of the Kripke construction PKF and Picollo (²⁰²⁰) shows that the same holds for attempts to recapture classical rules in the case glutty logics like LP.

The current proposal shows that nontransitive theories fare much better with respect to recapturing classical reasoning than ‘ordinary’ fully structural but non-classical theories. Restricting the structural rule of Cut allows us to formulate the restriction by absorbing the Cut rule of a classical theory and blocking it only whenever we apply a T-rule which goes beyond that classical theory. This strategy cannot work for a non-classical but structural approach. The derivation of the empty sequent via the Liar using the inversion principle shows that the only rule we need to apply after the T-inference is Cut.

STAT[S] does not only prove everything which our classical theory S proves. It strengthens the theory as it is transparent: it proves ϕ, Γ ⇒ Δ iff it proves T ⌜ϕ⌝, Γ ⇒ Δ and the same on the right hand side of the sequent arrow. Its conditional is also strong enough to capture this transparency in the object language by proving all conditionals of the form ⇒T ⌜ϕ⌝ ↔ ϕ (and its uniform formulation given function symbols for suitable substitution functions). Thus it may be argued that the current nontransitive approach combines the best of both worlds: a transparent truth-predicate and the proof-theoretic strength of classical theories.