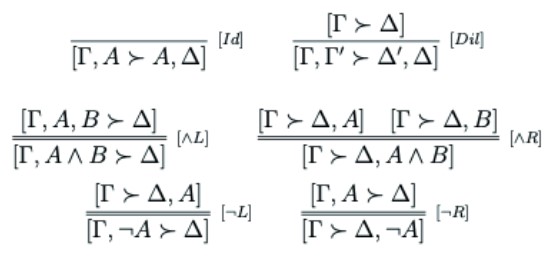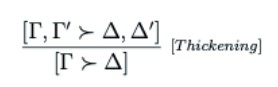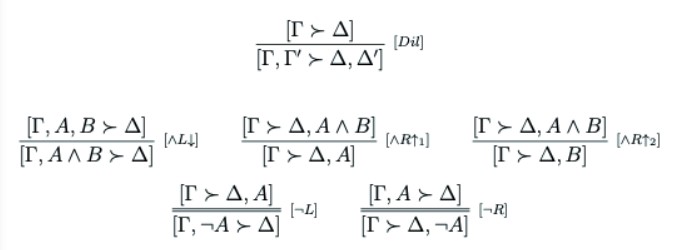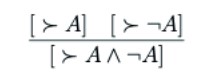In Uncut (²⁰¹⁸) Dave Ripley briefly compares his own position ¹ to that defended in French (2016), noting in UC§2.3.1 ² that: “it will emerge (...) that the distinct logical features exhibited by the formal approaches we respectively recommend in fact reveal, near enough, agreement about certain underlying phenomena.”

The kind of agreement which Ripley appears to have in mind here is one concerning how the two different approaches treat paradoxical sentences. According to the nonreflexive account of consequence given in French (²⁰¹⁶), the rejection of the structural principle [Id] is based around leaving open a position between accepting and rejecting a sentence; similarly on Ripley’s nontransitive account the rejection of the structural principle of [Cut] is based around leaving open a position between assertibility and deniability. In other words, both approaches agree that we should not ‘take a stand’ on paradoxical sentences, whether that means refraining from taking certain attitudes towards, or performing certain conversational acts with, such sentences. We get a difference in which structural principle to reject simply on the basis of how taking a stand on a sentence is connected up to the relevant notion of consequence.

Could the agreement about certain underlying phenomena be deeper than this, though? What I will explore here is one way in which one can see a deeper connection between the nontransitive logic defended by Ripley and nonreflexive logics, providing an example of an independently motivated nonreflexive notion of consequence living inside Ripley’s bilateralist meaning theory. I will begin in §1 by giving a brief summary of the elements of Ripley’s bilateralist meaning theory which will be most relevant in what follows. The bulk of the paper is in §2 which introduces a special kind of position which gives rise to a nonreflexive logic. In §3, finally, we will show how our special positions give rise to two interesting nonreflexive logics.

1. Positions, Bounds, and Consequence

Agents have points of view, and occasionally they choose to make their point of view public by asserting some sentences, and denying others. Call a pair [Γ : Δ] of sets of sentences asserted—Γ—and of sentences denied—Δ—a position. Not all positions are created equal, though. In particular some positions cohere in certain ways which other positions do not. Following Ripley let us call positions which are internally coherent in this way in bounds positions, and ones which fail to be internally coherent out of bounds positions.

According to Ripley, which positions are in or out of bounds is determined by our social practices of taking certain collections of assertions and denials to not appropriately cohere with one another, this being at least in part a material (as opposed to purely formal or structural) matter. In this respect, a position being out of bounds is related to Brandom’s notion of a pair of sentences being materially incoherent (Brandom, ²⁰⁰⁰), except lifted to govern pairs of sets of sentences rather than merely pairs of sentences. That having been said the bounds do, nonetheless, exhibit a variety of purely structural features, for example: ³

[Disjointness] If [Γ : Δ] is an in bounds position, then Γ ∩ Δ = ∅ (i.e. it is out of bounds to both assert and deny the same sentence).

[Say-Less] If [Γ,Γ’ : Δ,Δ’ ] is in bounds, then so is [Γ : Δ] (i.e. its always in bounds to say less)

The main goal of Uncut is to develop and defend a meaning theory constructed out of the above materials. The thought is that we can analyze the meanings of sentences and sentential operators in terms of the conditions under which assertions and denials of them are in, or out, of bounds. ⁴ The clearest example of how this is to work can be seen in the characterization of the meanings of the sentence connectives. For example, in UC§4.2.1 Ripley, following Restall (²⁰⁰⁵), argues that the bounds are also closed under the following conditions concerning the behaviour of ¬ and ∧: ⁵

[Assert ¬] [Γ : Δ,A] is in bounds iff [Γ, ¬A: Δ] is in bounds.

[Deny ¬] [Γ, A: Δ] is in bounds iff [Γ: Δ, ¬A] is in bounds.

[Assert ∧] [Γ, A, B: Δ] is in bounds iff [Γ, A ∧ B: Δ] is in bounds.

[Deny ∧] [Γ: Δ, A ∧ B] is in bounds iff [Γ: Δ, A] is in bounds or [Γ:Δ,B] is in bounds.

Another way of looking at the above constraints on the bounds is in terms of what Ripley calls bounds consequence, where a set of sentences Δ are a bounds consequence of a set of sentences Γ (= “Γ ⊩ Δ”) whenever the position [Γ: Δ] is out of bounds. The above conditions on in bounds positions correspond, in a very strong way, to the closure of bounds consequence under certain sequent rules. In particular, say that a rule R is correct for a consequence relation ⊢ ⁶ just in case whenever the premise sequents of R are in ⊢ then so is the conclusion sequent. What the above conditions on the behaviour of the bounds record, then, is that bounds consequence is closed under the rules in Figure 1. These are the rules for the sequent calculus which Ripley calls BC _¬∧ (UC§4.2.1).

Figure 1: The System BC¬∧  

We can distinguish between two different ways in which a calculus C is connected to a consequence relation ⊢. The calculus can be correct for ⊢, requiring that whenever the sequent [Γ≻Δ] is derivable in C that we have Γ⊢Δ, and the sequent can be rule-correct for ⊢, requiring that every rule R in C is correct for ⊢. What the above results tell us, then, is that the above calculus BC _¬∧ is correct for ⊩ because it is rule-correct for it.

One notably absent rule from the sequent calculus BC _¬∧ is the rule of [Cut]. For this rule to be correct for bounds consequence the bounds would have to be extensible in the sense that whenever [Γ : Δ] is in bounds then so is one of [Γ,A: Δ] or [Γ:Δ,A]. As is argued in UC§3.4, though, there is no reason to think, contra Restall (²⁰⁰⁵), that the bounds are extensible. ⁷ Moreover, according to Ripley, not only is there no reason to think that the bounds are extensible, but there are what seem to be counterexamples to extensibility—in particular, sentences like the Liar, or Curry sentences are ones for which both assertion and denial appear to be ruled out. Suppose, now, that an agent wants to stand by some position [Γ:Δ] and are asked whether A, where A is a sentence like the Liar which is a counterexample to extensibility. What can they do? Asserting or denying A would take their position out of bounds. What is needed is some act which the agent can perform which allows them to make clear that either asserting or denying A will take their position out of bounds. To this end Ripley distinguishes between two different species of speech acts: tolerant assertion and denial, and strict assertion and denial. Strict assertions and denials are just what we’ve been calling assertions and denials thus far, these are the assertions and denials which constitute positions. Tolerant assertions and denials are acts which, rather than constituting positions, constrain their evolution. A tolerant assertion of A is incompatible with the (strict) denial of A, and similarly a tolerant denial of A is incompatible with the (strict) assertion of A. One way of cashing out this talk of incompatibility is the following:

• A tolerant assertion of A relative to a position [Γ:Δ] says that the position [Γ:Δ,A] is out of bounds.

• A tolerant denial of A relative to a position [Γ:Δ] says that the position [Γ:Δ,A]is out of bounds.

Tolerant acts allow us to articulate our answer to the question of whether A, when A is a sentence like the Liar—we can both tolerantly assert it, communicating that it is undeniable, and tolerantly deny it, communicating that it is unassertible.

2. Umbral Positions

As we have been putting things here, positions are constituted by strict assertions and denials, and merely constrained by tolerant acts. Given that tolerant assertions are not present in positions (at least as we have described them here, and as they are described in Uncut), in order to give a fuller theory of the normative structure of discourse we ought to also be keeping track of which sentences have been tolerantly asserted and denied. There are two different ways in which this could be done: either we could explicitly keep track of tolerant assertions and denials (and give analogues of the above conditions for tolerant acts), or we could understand the behaviour of tolerant acts in a derivative manner, in terms of how they constrain positions. Here we will investigate the prospects for the latter project for understanding tolerant acts.

To this end call a pair ⟨⟨Σ:Θ⟩⟩ of tolerant assertions Σ and tolerant denials Θ an umbral position. In a similar way to how a shadow can give us imprecise information about the object casting it, so too can umbral positions give us imprecise information about the structure of a position through the relation of shadowing. In order to introduce the notion of shadowing we have in mind, we will first need some definitions from Uncut §2.4.2.

Given two positions P=[Γ:Δ] and P’=[Γ’:Δ’] let the position P⊔P’=[Γ,Γ’:Δ,Δ’ ].

Definition 2.1 (Equivalence of Positions) Two positions [Γ:Δ] and [Γ’:Δ’ ] are equivalent (written [Γ:Δ]≃[Γ’:Δ’ ]) iff for all positions P we have that [Γ:Δ]⊔P is in bounds iff [Γ’:Δ’ ]⊔P is in bounds.

That is to say, two positions are equivalent if they leave open the same possibilities for in-bounds expansions. In Uncut Ripley then uses this notion of equivalence to define implicit assertion and denial.

Definition 2.2 Let [Γ:Δ] be a position, and A a sentence. Then

• [Γ:Δ] implicitly asserts A (= [Γ:Δ]⊳A) iff [Γ:Δ] is equivalent to [Γ,A:Δ], and

• [Γ:Δ] implicitly denies A (= [Γ:Δ]⊲A) iff [Γ:Δ] is equivalent to [Γ:Δ,A]

Say that [Γ:Δ] implicitly contains [Γ’:Δ’] just in case we have [Γ:Δ]≃[Γ,Γ’:Δ,Δ’]. It is worth noting that this is equivalent to [Γ:Δ] implicitly asserting each formula in Γ’, and implicitly denying each formula in Δ’. ⁸

Definition 2.3 (Shadowing) An umbral position ⟨⟨Σ:Θ⟩⟩ is a shadow of the position [Γ:Δ] iff Σ∩Δ’=∅ and Θ∩Γ’=∅ for any [Γ’:Δ’ ] implicitly contained in [Γ:Δ].

That is to say, a umbral position shadows any position which does not implicitly assert a sentence which it tolerantly denies, and does not implicitly deny any sentence which it tolerantly asserts. An alternative way of putting this is that an umbral position ⟨⟨Σ:Θ⟩⟩ is a shadow of [Γ:Δ] iff for all A∈Θ we have [Γ:Δ]⋫A, and for all B∈Σ we have [Γ:Δ]⋪B. This more directly spells out the sense in which, when an umbral position shadows a position whenever that position obeys the constraint encoded in the umbral position.

Given that it will often be more convenient to work with this alternative formulation it is a worthwhile exercise in understanding implicit assertion and denial to show that they are equivalent.

Proposition 2.4 ⟨⟨Σ:Θ⟩⟩ is a shadow of [Γ:Δ] iff for all A∈Θ we have [Γ:Δ]⋫A,and for all B∈Σ we have [Γ:Δ]⋪B.

Proof. For the ‘only if’ direction suppose that ⟨⟨Σ:Θ⟩⟩ is a shadow of [Γ:Δ], but that the RHS condition is not met. So, without loss of generality, we must have [Γ:Δ]⊳A for some A∈Θ. That is to say, we have [Γ:Δ]≃[Γ,A:Δ], which is to say [A:] is implicitly contained in [Γ∶Δ ]. But then as ⟨⟨Σ:Θ⟩⟩ is a shadow of [Γ:Δ] we must have A∩Θ=∅, which is impossible as A∈Θ. So it follows that the RHS condition is met.

For the ‘if’ direction suppose that the RHS condition is met, but we have a position [Γ’:Δ’ ] implicitly contained in [Γ:Δ], while either Γ’∩Θ≠∅ or Δ’∩Σ≠∅. Without loss of generality, suppose that Δ’∩Σ≠∅, and so there is a B∈Δ’ such that B∈Σ. Then in particular we also must have [Γ:Δ]⊳B. But by the RHS condition as B∈Σ we must have [Γ:Δ]⋫B, which is impossible. So it follows that ⟨⟨Σ:Θ⟩⟩ is a shadow of [Γ:Δ]. □

Given this result we will freely move between these two different ways of spelling out what it takes for an umbral position to shadow a position.

Let us now look at a few simple properties of the shadowing relation which are reminiscent of the norms on assertion and denial which govern positions.

Proposition 2.5 (Weakening) If ⟨⟨Σ,Σ’:Θ,Θ’ ⟩⟩ shadows a position [Γ:Δ], then ⟨⟨Σ:Θ⟩⟩ shadows [Γ:Δ].

Proof. Suppose that ⟨⟨Σ,Σ’:Θ,Θ’ ⟩⟩ shadows a position [Γ:Δ]. Then we have that [Γ:Δ]⋪σ for every σ∈Σ∪Σ’, and [Γ:Δ]⋫θ for every θ∈Θ∪Θ’. But from this it follows directly that [Γ:Δ]⋪σ for every σ∈Σ and [Γ:Δ]⋫θ for every θ∈Θ, and so it follows by Proposition 2.4 that ⟨⟨Σ:Θ⟩⟩ shadows [Γ:Δ], as desired.

This is just a straightforward result of the fact that shadowing is intended to be tracking how positions are constrained. If a position is constrained by a more stringent restriction on its in-bounds evolution, then it is also constrained by any less-stringent restriction.

Let us now look at the behaviour of negation under the shadowing relation. For this we will need to make use of the following result concerning when a position fails to implicitly assert a sentence.

Proposition 2.6 [Γ:Δ]⋪A iff there exists a position P_A s.t. (i) [Γ:Δ]⊔P_A is in bounds, and (ii) [Γ:Δ,A]⊔P_A is out of bounds.

Proof. Suppose, for the ‘only if’ direction, that [Γ:Δ]⋪A. For this to be the case it must be that [Γ:Δ] is not equivalent to [Γ:Δ,A], and so there exists a position P_A s.t. either (i) or (ii) below obtain.

(i) [Γ:Δ]⊔P_A is in bounds & [Γ:Δ,A]⊔P_A is out of bounds

(ii) [Γ:Δ]⊔P_A is out of bounds & [Γ:Δ,A]⊔P_A is in bounds

But (ii) above implies that [Γ:Δ]⊔P_A is out of bounds, and so by the contrapositive of [Say-Less] that [Γ:Δ,A]⊔P_A is out of bounds, contradicting the second conjunct of (ii). So it follows that if [Γ:Δ] is not equivalent to [Γ:Δ,A] that (i) must obtain, as desired.

The ‘if’ direction follows from the definition of equivalence for positions, and implicit assertion.

Proposition 2.7 ⟨⟨Σ,A:Θ⟩⟩ is a shadow of a position [Γ:Δ] iff ⟨⟨Σ:Θ,¬A⟩⟩ is a shadow of a position [Γ:Δ]

Proof. Suppose that ⟨⟨Σ,A:Θ⟩⟩ is a shadow of a position [Γ:Δ]. Then this means that (a) [Γ:Δ]⋫θ for all θ∈Θ, (b) [ Γ : Δ ]⋪σ for all σ∈Σ, and (c) [Γ:Δ]⋪A. From (c) and Proposition 2.6 it follows that there is a position P such that (i) P⊔[Γ:Δ] is in bounds, and (ii) P⊔[Γ,A:Δ] is out of bounds. So by (ii) and [Deny¬] it follows that P⊔[Γ:Δ,¬A] is out of bounds, and so by (i) and Proposition 2.6 again, that [Γ:Δ]⋫¬A. But from this along with (a) and (b) it follows that ⟨⟨Σ:Θ,¬A⟩⟩ is a shadow of a position [Γ:Δ], as desired.

The ‘if’ direction follows similarly.

Proposition 2.8 ⟨⟨Σ:Θ,A⟩⟩ is a shadow of a position [Γ:Δ] iff ⟨⟨Σ,¬A:Θ⟩⟩ is a shadow of a position [Γ:Δ]

We will also find it useful to make use of the following results concerning conjunction below.

Proposition 2.9 If ⟨⟨Σ,A∧B:Θ⟩⟩ is a shadow of a position [Γ:Δ], then ⟨⟨Σ,A,B:Θ⟩⟩ is a shadow of a position [Γ:Δ].

Proof. Suppose that ⟨⟨Σ,A∧B:Θ⟩⟩ is a shadow of a position [Γ:Δ]. Then this means that (a) [ Γ : Δ ]⋫θ for all θ∈Θ, (b) [Γ:Δ]⋪σ for all σ∈Σ, and (c) [ Γ : Δ ]⋪A∧B. From (c) by Proposition 2.6 it follows that there is a position P such that (i) P⊔[Γ:Δ] is in bounds, and (ii) P⊔[Γ:Δ,A∧B] is out of bounds. So by (ii) and [Deny∧] it follows that both (iii) P⊔[Γ:Δ,A] is out of bounds, and (iv) P⊔[Γ:Δ,B] is out of bounds. So by Proposition 2.6 (i) and it follows that [Γ:Δ]⋪A and [Γ:Δ]⋪B, which combined with (a) and (b) entails that ⟨⟨Σ,A,B:Θ⟩⟩ is a shadow of a position [Γ:Δ], as desired. □

Proposition 2.10 If ⟨⟨Σ:Θ,A⟩⟩ shadows the position [Γ:Δ], then ⟨⟨Σ:Θ,A∧B⟩⟩ shadows the position [Γ:Δ]

Proof. Suppose that ⟨⟨Σ:Θ,A⟩⟩ is a shadow of a position [Γ:Δ]. Then this means that (a) [Γ:Δ]⋫θ for all θ∈Θ, (b) [ Γ : Δ ]⋪σ for all σ∈Σ, and (c) [Γ:Δ]⋫A. So from (c) and Proposition 2.6 it follows that we have a position P such that (i) P⊔[Γ:Δ] is in bounds, and (ii) P⊔[Γ,A:Δ] is out of bounds. From (ii) by [Say-Less] it follows that P⊔[Γ,A,B:Δ] is out of bounds, and so by [Assert∧] that P⊔[Γ,A∧B:Δ] is out of bounds. But from this and (i) it follows that [Γ:Δ]⋫A∧B and so by (a) and (b) that ⟨⟨Σ:Θ,A∧B⟩⟩ shadows the position [Γ:Δ], as desired.

3. Consequence

How should we connect up the notion of an umbral position to some notion of consequence? There are a number of options which we could consider, but we will look at two straightforward and interesting candidates here: position-relative consequence, and umbral bounds consequence. Most of our focus will be on the latter of these.

3.1. Position-relative consequence

Position-relative consequence is a notion of consequence which is relativised to some fixed position P.

Definition 3.1 Let P be a position, and Γ and Δ be sets of sentences. Then Δ is a P-relative consequence of Γ (=Γ ⊩P Δ) iff ⟨⟨Γ: Δ⟩⟩ shadows P.

Position-relative consequence, then, records those constraints on positions which are obeyed by P. If P is not the empty position [∅:∅] then ⊩ ^P will fail to be reflexive. Why? Because as P is non-empty there must be some sentence A such that P⊳A or P⊲A (because P=P⊔[A:∅] or P=P⊔[∅:A]). But this means that ⟨⟨A:A⟩⟩ will not shadow P, and so by the above definition we will have A⊮^P A.

One curious property of position-relative consequence is that the rule of [ Thickening ] is correct for it.

The correctness of this rule for ⊩ ^P follows directly from Proposition 2.5. As noted just after Proposition 2.5, given that ⟨⟨Γ,Γ’:Δ,Δ’ ⟩⟩ places a stronger restriction on positions than ⟨⟨Γ:Δ⟩⟩, if a position obeys the stronger condition it will also obey the weaker.

Position-relative consequence is an unfamiliar looking beast, even at only a purely structural level, so we will leave it aside now to look at a notion of consequence which looks slightly more familiar.

3.2. Umbral-bounds consequence

When should we say that an umbral position is out of bounds? One relatively obvious candidate definition is the following: say that an umbral position is out of bounds whenever the proscription on the bounds which it records is not obeyed by all in bounds positions. That is to say, an umbral position ⟨⟨Σ:Θ⟩⟩ is out of bounds iff there is some in bounds position P which it doesn’t shadow. With a notion of when it is that an umbral position is out of bounds, we can now give a definition of bounds consequence for umbral positions as follows.

Definition 3.2 (Umbral-Bounds Consequence) Σ⊩^B Θ iff there is an in bounds position P such that ⟨⟨Σ:Θ⟩⟩ does not shadow P.

The first thing which is worth noting is that Umbral-Bounds consequence is non-reflexive.

Proposition 3.3 λ⊮^B λ where λ is any sentence (like the Liar) where both [λ:∅] and [∅:λ] are out of bounds.

Proof. We show that the umbral position ⟨⟨λ:λ⟩⟩ shadows every in bounds position. Suppose that P is an in bounds position. What we need to show is that P⋫λ and P⋪λ. Suppose, then, that P⊳λ. Then by the definition of ⊳ we have P≃P⊔[λ:]. But as [λ:] is out of bounds, it follows that P⊔[λ:] is out of bounds, and so as P≃P⊔[λ:], that P is also out of bounds. But by hypothesis P is in bounds. So by reductio P⋫λ. A similar argument delivers that P⋪λ, and from this the result follows.

Here we can see the desired agreement on underlying reality—any sentence which is a counterexample to the extensibility of the bounds, is also a counterexample to the reflexivity of the Umbral-bounds. At this point Umbral-Bounds Consequence looks very similar to the kind of system advocated for in French (²⁰¹⁶). For example, the contrapositives of Propositions 2.5, 2.7, 2.8, 2.9 and 2.10 can be used to show that the calculus in Figure 2 is rule-correct for ⊩^B.

Figure 2: A calculus which is rule-correct for ⊩ ^B  

This is where the similarities to this kind of system end, though. To see this first consider the following result concerning Umbral-Bounds consequence.

Proposition 3.4 Suppose that Γ∪Δ≠∅. Then, if [Γ:Δ] is in bounds, then Δ⊩^B Γ.

Proof. Suppose, for a reductio, that [Γ:Δ] is in bounds, but that Δ⊮B Γ. From this last claim it follows that for all in bounds positions P, that ⟨⟨Δ:Γ⟩⟩ shadows P. So in particular it follows that ⟨⟨Δ:Γ⟩⟩ shadows [Γ:Δ]. But this requires that Δ∩Δ=∅ and Γ∩Γ=∅ (as [Γ:Δ] implicitly contains itself), which is impossible as at least one of Γ and Δ must be non-empty. So the result follows.

This result has a number of direct consequences.

• If asserting A by itself will not take you out of bounds (in the sense that [A:∅] is not out of bounds) then ⊩^B A.

• If denying A by itself will not take you out of bounds (in the sense that [∅:A] is not out of bounds) then A⊩^B.

• If A can be asserted, or denied without going out of bounds, the A⊩^B A.

Under the reasonable assumption that for at least one sentence A the positions [A:∅] and [∅:A] are in bounds, we can also see that a number of rules which are valid in the system advocated for in French (2016) are not correct for ⊩^B.

Proposition 3.5 Under the above assumption [Cut] is not correct for ⊩B.

Proof. Note that the umbral position ⟨⟨∅:A⟩⟩ is out of bounds because it fails to shadow [A:∅], and the umbral position ⟨⟨A:∅⟩⟩ is out of bounds because it fails to shadow [∅:A], while the umbral position ⟨⟨∅:∅⟩⟩ is in bounds, as it shadows every position. So [Cut] is not correct for ⊩B. □

Proposition 3.6 Under the above assumption [∧R↓] is not correct for ⊩^B.

Proof. Consider the following instance of [∧R↓]

Under the above assumption it follows that ⊩^B A and A⊩^B, and so by [¬R] that ⊩^B¬A. But in order to have ⊩^B A∧¬A we would need an in bounds position P such that P⊲A∧¬A. But as [A∧¬A:]≃[A:A] by [Assert∧] and [Assert¬] this would mean that P≃P⊔[A:A], which cannot be the case, as P⊔[A:A] is out of bounds regardless of what P is, and so in particular will be out of bounds even if P is in bounds!

From this it follows that the notion of ‘conjunction’ that lives in the bounds (at least according to Umbral-Bounds Consequence) is not the standard notion of conjunction—we’ve only been told when we can conclude that a tolerant assertion of a conjunction is out of bounds, and what we can conclude from the tolerant denial of a conjunction being out of bounds. If Umbral-Bounds consequence has a story to tell about when, for example, tolerant denial of a conjunction is out of bounds it cannot be the standard story.

4. Conclusion

In order to fully explain the behaviour of positions, and how they interact with the bounds, any advocate of a meaning theory like the one presented in Uncut will need to have some mechanism to register the tolerant assertions and denials which agents make. What we have done here is to investigate the extent to which this can be done solely using the formal materials which take centre stage throughout Uncut—positions. What we have seen here is the extent to which we can fruitfully understand tolerant acts as parasitic on the behaviour of their strict cousins. As we mentioned earlier, though, this is not the only option available for the bilateralist. They could instead attempt to understand tolerant acts directly saying what it is for complex tolerant acts to constrain further strict and tolerant acts.

What I hope to have shown is that there are independently well motivated logics living within the bounds, lurking withing the shadows of positions, and along the way have shed some light on the way in which nonreflexive and nontransitive logics can arise given agreement on underlying features of the world and our assertions about it.