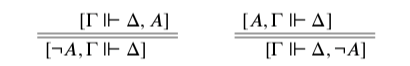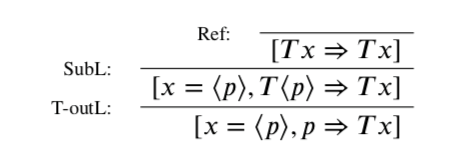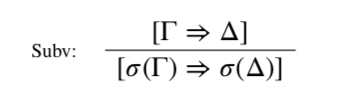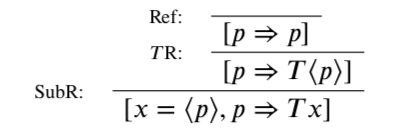Metainferences in Uncut

However, it’s not like it’s accidental that Uncut looks in some depth at sets of sequents. I aim to give a precise and workable framework for theorizing about natural-language meaning in terms of positions, and when positions are in or out of bounds. Since positions are basically just sequents, thinking about which positions are out of bounds amounts to thinking about a set of sequents. So sets of sequents are definitely important to my project in Uncut.

Moreover, the metainferences such sets are or are not closed under also play an important role. For example, a compositional semantics for negation in this framework gives the conditions under which a position involving an assertion or denial of ¬A is out of bounds, in terms of the conditions under which a position involving an assertion or denial of A is out of bounds. Uncut puts forward the semantics according to which an assertion of ¬A is out of bounds whenever a denial of A is, and a denial of ¬A is out of bounds whenever an assertion of A is. Using [Γ⊩Δ] to indicate that the position [Γ⇒Δ] is out of bounds, and using the double horizontal line for ‘if and only if,’ this semantics can be expressed like so:

So metainferences too are definitely important to the project; they’re the very terms in which I give compositional semantics to various pieces of vocabulary.

I don’t see that metametainferences, or higher metainferences than that, have any particular importance to the project of giving semantics for natural language. I’m not particularly invested in this claim, though; indeed, I’d probably prefer it if it turns out to be wrong, since that would be more interesting! But for now that’s how things look to me. (Barrio & Pailos certainly don’t offer any arguments to the contrary; they don’t consider natural language semantics at all, as far as I see.)

The formal tools I draw on and develop in Uncut reflect this approach. These tools work with sets of sequents and level-1 metainferences, and ignore higher metainferences entirely. If Barrio & Pailos are right about when logics are distinct, that means that my work in Uncut fails to focus in on any single logic. That’s fine with me; I don’t claim otherwise, and as far as I can tell nothing hangs on it.

Lemma 1.2

Above I referred to STAT[S] as ‘naive’ rather than ‘transparent.’ By this I mean what Dittrich notes in their penultimate sentence: that the sequent [⇒T⟨ϕ⟩↔ϕ] is derivable in STAT[S] for every ϕ. This is already a lot; adding a full rule of cut to STAT[S] would render it trivial. However, it is not yet full transparency; and indeed, I’m not sure that STAT[S] really is fully transparent.

STAT is the set-set sequent calculus for ℒ_T consisting of reflexivity, the rules ≠ and =, ¹ the connective rules for ¬,⊃,∀, the substitution rules Sub, the Robinson rules Q1–Q7, the induction rule Ind, ² Cut for arithmetic formulas only, and the T-insertion rules TL and TR.

Lemma 1.2 claims that T-outL and T-outR are admissible in STAT, where these are the converses of TL and TR, respectively. I don’t know this claim to be false, but I don’t believe the given proof succeeds. Consider the following application of T-outL:

In terms of understanding Dittrich’s given proof, a question arises: does the T⟨p⟩ that results here from the rule SubL count as principal or not? However, whether or not this occurrence counts as principal, the given proof does not show how to eliminate this use of T-outL. If this occurrence counts as principal, we are told ‘the conclusion is immediate’; while this is certainly so if the occurrence is principal in an application of TL or TR, it is not so here. On the other hand, if this occurrence does not count as principal, we are told ‘simply apply the Induction Hypothesis’ to the line [Tx⇒Tx]. However, this line is not of the right form for this; it applies the truth predicate T to the variable x, where the rule T-outL we’re working with only concerns applications of T to certain numerals.

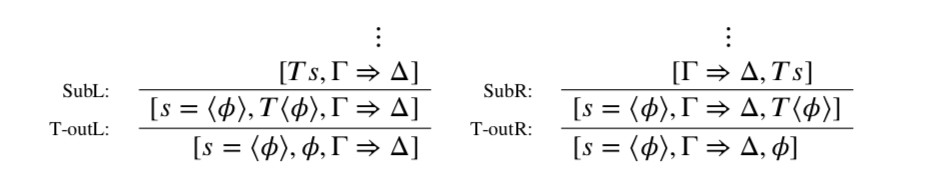
In general, the derivations I worry about are those ending in one of the following forms:

Here, the inductive step only seems to work in case the term s is the numeral of the code of ϕ. In other cases, either we can’t apply the T-out rule at all (in case s is not the numeral of the code of any formula), or else the wrong result sequent is produced (in case s is the numeral of the code of some other formula).

Some of the time this is repairable. In particular, Dittrich (²⁰²⁰) shows how to handle the case where s is a closed term not denoting the code of ϕ; in this case the rule ≠ makes the needed final sequent an initial sequent.

In addition, for cases like the above example, in which the key term s is a variable, there is also a repair. STAT has the convenient (and usual) property that where σ is any substitution of arbitrary terms for variables, then the following rule is height-preserving admissible: ³

Wlog, focus on the left form of the trouble case. If s is a variable, then since [Ts,Γ⇒Δ] is derivable, so is [T⟨ϕ⟩,σ(Γ)⇒σ(Δ)], where σ is the substitution of ⟨ϕ⟩ for the variable s. Moreover, this latter can be derived in the same number of steps. So we can apply the inductive hypothesis to get a proof of [ϕ,σ(Γ)⇒σ(Δ)]. Now repeated applications of SubL and SubR can bring us to a derivation of [t=⟨ψ⟩,ψ,Γ⇒Δ]. ⁴

Applying this strategy to the above example, and handling the initial sequent exactly as Dittrich explains, yields the following derivation:

Taking stock, we have seen that the proof can be made to work when s is the numeral of the code of ϕ, when s is a closed term not denoting the code of ϕ, and when s is a variable. This leaves two cases open: when s is a closed term denoting the code of ϕ but not the numeral for this code, and when s is an open term other than a variable. I don’t have quick fixes for either of these cases, but neither do I have a demonstration that the Lemma fails (and indeed I wouldn’t be too surprised if it holds). For now, then, I think we still don’t know whether Dittrich’s systems are truly transparent—and myself, I wouldn’t want to guess.

Let me, then, briefly consider each of two possibilities: first, that these systems are indeed transparent, or that adding transparency to them would not yield triviality; and second, that they are not transparent, and adding transparency would yield triviality. ⁵

First, let’s suppose that Dittrich’s systems really do feature a transparent truth predicate, or that transparency can be added to them without triviality. If this is so, then it seems to me Dittrich has built, or at least pointed the way towards, something very special: a transparent truth predicate added to classical arithmetic in a way that remains nontrivial while allowing for the formation of paradoxes of all sorts, and also allows us to reach the bewildering heights of proof-theoretic strength achieved by nontransparent axiomatic theories of truth.

Now, I myself happen not to care a great deal about proof-theoretic strength. I’m in it for the natural-language semantics, and the strength can fall where it may. But it’s worth noticing that the central argument given against transparent truth by advocates of nontransparent axiomatic theories is based entirely on proof-theoretic strength. ⁶ This kind of strength may not matter for my purposes, but it certainly does for theirs.

That is, advocates of nontransparent axiomatic theories of truth don’t really seem to value, make use of, or even really care about the nontransparency directly. They’re optimizing for something else—proof-theoretic strength—and their key argument against transparent truth is that it gets in the way of this optimization. However, that argument has always proceeded by way of examples. If Dittrich’s systems are transparent, or can be made to be, then they show that this conflict between transparency and proof-theoretic strength was only an appearance created by a particular choice of examples. Truth theorists concerned about proof-theoretic strength, even those willing to let proof-theoretic strength outweigh all other considerations, would for the first time have transparent systems to study as well. This would be a major breakthrough, and if you ask me which possibility I hope is correct about Dittrich’s systems, it’s this one.

Second, let’s suppose that Dittrich’s systems are not in fact transparent, and that adding transparency to them would result in triviality. This would also be a fascinating outcome. Recall that Dittrich’s systems by definition include TL and TR, are fully naive, and are certainly not trivial. So we would still have a significant advance on the state of the art: the only other theories of truth we have with anything like this proof-theoretic strength are not only nontransparent, but also non-naive, and not closed under both TL and TR. So even if Dittrich’s systems cannot be brought all the way to full transparency, they still provide a breakthrough of roughly the same kind.

However, if things do turn out to go this way, additional questions (and hopefully answers) arise as well. Just what is it that gets in the way of transparency? It’s been thought that even naivete would get in the way of this kind of strength, and Dittrich’s systems already show us that this was a mistake. So if theorists turn out to have been right about transparency conflicting with this kind of strength, they must have been right for the wrong reasons. If we found out that Dittrich’s systems could not be made transparent, this would hopefully set us on the path to appreciating the right reasons.

Whatever the situation turns out to be regarding the transparency of Dittrich’s systems, then, I think this is exciting work, pointing the way towards a promising new family of systems for blending truth and arithmetic.

Which bounds?

By ‘out of bounds,’ Ferguson means something much broader than the understanding I put forward in Uncut. They understand a position to be out of bounds when ‘to adopt this position is to flout conversational norms in some way.’ That’s definitely not the understanding of the bounds I develop in Uncut. So at least some of what Ferguson’s article casts as disagreement seems to me much more like changing the subject.

The subject Ferguson raises—the totality of conversational norms—is certainly an interesting one! In a moment, I’ll respond a bit to what they say about this notion. First, though, I think it’s a good idea to take a crack at explaining how Uncut develops the idea of the bounds, since it certainly isn’t this. ⁷

The bounds I am concerned with in Uncut are certainly set by conversational norms, but not just any conversational norm is relevant. The idea is rather this: one important aspect of our conversational practices involves attributing positions to each other. We do this as a way to understand each other’s point of view. Moreover, at least some conversational moves require this for their appropriateness; it’s not felicitious to assert ‘You’re wrong; I didn’t eat it’ in a conversational context without attributing some commitment to ‘You’ to the effect that the speaker did eat it.

Attributing these positions to each other, though, is not simply a matter of keeping track of what’s actually happened. We also hold each other to norms of coherence or fit. Sometimes a position simply doesn’t fit together; it clashes with itself. The norms I’m concerned with are these norms of fit in particular.

I certainly agree with Ferguson that these norms don’t exhaust all conversational norms. One way to see this is to look at how these norms are enforced. When someone seems to have adopted a position that doesn’t fit together in the course of a conversation, they can be corrected. This correction can take many forms; I mention some of the most usual in the precis: reinterpretation (often by way of hypothesizing an ambiguity), asking for clarification, and outright dismissal. These corrections are all forms of norm enforcement.

These kinds of corrections, though, are not appropriate responses to violations of politeness or secrecy norms like the violations Ferguson focuses on. Supposing a context in which uttering ‘fuck’ violates a politeness norm, if A asserts ‘Dave is a fuckhead’ (or for that matter ‘Dave is not a fuckhead’), they’re clearly in violation of a conversational norm. Now, consider five possible responses someone might make to such an utterance:

1. I don’t appreciate that kind of language.

2. I know what you mean, but do you have to say it like that?

3. Maybe you mean that Dave is lovely?

4. Do you mean always, or only at conferences?

5. That doesn’t make any sense; you’re just spouting garbage.

Of these five, only 1 and 2 would normally serve as appropriate attempts to enforce the politeness norm.

An attempt to reinterpret A’s assertion, as in 3, is not really a sensible way to try to enforce the norm against saying ‘fuck.’ I note that there is a reading we can give to the sentence in 3 where it’s a suggestion to A that they should communicate the same message as ‘Dave is a fuckhead’ through irony, by uttering ‘Dave is lovely’ ironically. On this reading, it can be an appropriate attempt to enforce the norm against saying ‘fuck.’ But on this reading, it’s not an attempt at reinterpretation at all.

An attempt to clarify A’s meaning, as in 4, doesn’t do anything at all to enforce the norm against saying ‘fuck’; it just takes A’s utterance in stride. And outright dismissal, as in 5, is more or less the same; it also isn’t an appropriate way to enforce the norm.

So politeness norms, like the norms Ferguson considers, are enforced through totally different mechanisms from the norms of coherence or fit I focus on in Uncut. Secrecy norms are enforced through different mechanisms yet again. Ferguson’s conception of the bounds, then, is just a different, and much broader, conception than the one I’m focused on. I think it’s a mistake to see this as a disagreement at all; there are just different topics here. ⁸

Secrecy and weak Kleene

As I’ve pointed out above, Ferguson’s topic—the totality of conversational norms—is not my topic in Uncut. But it’s a fascinating topic, and it’s exciting to see the logical work they develop to explore the idea.

I think Ferguson is right to say that usual analogies between quantifiers and connectives should fail, if we are focused on the totality of conversational norms. This is because the analogy relies on seeing instances of quantified sentences as analogous to components of compound sentences. But instances of quantified sentences do not occur in those quantified sentences, while the components of compound sentences do occur in the compounds. Since at least some conversational norms—for example politeness, as Ferguson points out—are sensitive to occurrence, they do not treat these cases alike. ⁹ Thus, any logical approach we develop should also not treat these cases alike.

However, I want to look in a bit more detail at Ferguson’s password examples, and in particular how these examples relate to disjunction. I think they’re too hasty to hold to a weak Kleene theory of disjunction here. The reason is that secrecy is not quite like politeness in how it handles occurrences. Let me start by setting out some points of agreement: if the password is ‘marriedcowboy,’ then I agree with Ferguson that it violates secrecy norms to assert ‘The password is “marriedcowboy”,’ to assert ‘The password is not “marriedcowboy”,’ and to assert ‘Either the password is “marriedcowboy” or it’s “uglyduckling”.’ Moreover, it doesn’t violate any secrecy norm to assert ‘There exists a password.’

However, Ferguson maintains that it would violate secrecy norms to assert any finite disjunction of the form ‘The password is X or the password is Y or the password is Z or …,’ as long as ‘marriedcowboy’ is somewhere among X, Y, Z, …. This is not an incidental commitment; it follows directly from the weak Kleene treatment of disjunction. If secrecy did work like politeness, moreover, this would be true; if there’s a norm against saying ‘fuck,’ then saying it once in the middle of a long disjunction still violates that norm.

However, real password systems feature only finitely many possible passwords. Often, a maximum password size will be fixed by the developer of the password system, but the mere fact that computer systems have to work with finite resources is sufficient to guarantee that there is always some maximum size for working passwords, no matter the system. Moreover, it’s easy to arrive at upper bounds on the maximum size. For example, Hilbert and López (²⁰¹¹) estimates that in 2007, the total digital data storage capacity on Earth was around 300 exabytes, or 3×10²⁰ bytes. Even today, no doubt, no password system supports passwords of this length.

Because of this, there are finite disjunctions of the form ‘The password is X or the password is Y or the password is Z or …,’ where X, Y, Z, … exhaust all possible passwords. Such disjunctions are not practically possible to assert, of course; for any realistic password system they come out way too long. But not all assertions of such disjunctions violate secrecy norms. ¹⁰ Indeed, asserting such a disjunction doesn’t amount to much more than asserting ‘There exists a password.’ If that’s right, then the weak Kleene treatment of disjunction Ferguson adopts doesn’t correctly track the norms in play. Disjunctions over known finite domains really are a lot like particular quantifications.

What logical tools could we use, then, to explore this issue? They won’t be value-functional, I think, at least if there is only one value in use to represent ‘norm-violating.’ This is because at least some disjunctions of false claims with norm-violating claims are themselves norm-violating, as Ferguson points out, while at least some disjunctions of false claims with norm-violating claims are not, as I’ve pointed out. I won’t enter into the project of trying to build a better model here; I just want to call attention to the fact that the weak Kleene approach seems to oversimplify the issue.

A different approach

There’s something a bit odd, I think, about counting an umbral position as out of bounds if there’s just some in-bounds position it doesn’t shadow. For example, take some claim p that can be either asserted or denied on its own without violating the bounds, like ‘I like hamburgers’ or something. That is, take some p where both [p⇒] and [⇒p] are in bounds. Note that ⌊:p⌋ does not shadow [p⇒], and that ⌊p:⌋ does not shadow [⇒p]. So on French’s understanding, both ⌊:p⌋ and ⌊p:⌋ are out of bounds. This seems at least a bit weird: tolerant acts are meant to be weaker than their corresponding strict acts, and yet here we’re counting strict acts as in bounds where their corresponding tolerant acts are not.

A different choice would be to count an umbral position as out of bounds when every in-bounds position isn’t shadowed by it. Going this way would mean that we’d count an umbral position as out of bounds only when there’s no in-bounds position that obeys its constraints. Supposing, as both French and I do, that the bounds on positions are closed under dilution, this is equivalent to counting an umbral position as out of bounds iff it does not shadow the empty position [⇒]—and that’s the understanding I’ll work with, since it’s simpler.

On this understanding, tolerant acts indeed do come out as weaker than their corresponding strict acts. Suppose, for example, that ⌊p:⌋ is out of bounds in this new sense, that it does not shadow [⇒]. Then [⇒] implicitly denies p. Thus, [p⇒] must be equivalent to [p⇒p]; since the latter is out of bounds, so is the former. That is, when a tolerant assertion is out of bounds, its corresponding strict assertion is as well; the same goes for denials.

This also gives us a new consequence relation based on bounds on umbral positions. Say that Σ⊩^z Θ iff the umbral position ⌊Σ:Θ⌋ does not shadow the empty position. There are a lot of similarities between ⊩^B and ⊩^z. For example, ⊩^z also obeys all the rules French displays for ⊩^B. But there are also differences.

Both are not reflexive, but ⊩^z more so. We only have A⊩^z A when the empty position implicitly asserts or denies A. It takes a lot for the empty position to implicitly assert A: that means that asserting A could never bring any in-bounds position out of bounds, that assertions of A don’t clash with anything at all. (Similarly if the empty position denies A.) Without getting too committal about the bounds, I think it’s safe to say that most sentences are not like this.

Moreover, none of Propositions 3.4 through 3.6 hold of ⊩^z. For example, suppose that the position [p⇒q] is in bounds. That gives no reason to think that either the empty position implicitly asserts p or it implicitly denies q. The bounds themselves might have nothing at all to say here. If that’s so, however, then q⊩/ ^z p, so Proposition 3.4 does not hold of ⊩^z.

Proposition 3.5 shows that ⊩^B is not closed under cut. But ⊩^z, on the other hand, is closed under cut, as long as we suppose that the empty position itself is in bounds. To see this, suppose that Σ⊩^z Θ,A and A,Σ⊩^z Θ. That is, neither ⌊Σ:Θ,A⌋ nor ⌊A,Σ:Θ⌋ shadows the empty position. So either: the empty position implicitly asserts some θ∈Θ, or it implicitly denies some σ∈Σ, or it both implicitly asserts and implicitly denies A. In either of the first two cases, ⌊Σ:Θ⌋ does not shadow the empty position for the same reason. In the third case, the empty position must be out of bounds already—which we’ve supposed is not the case. So Σ⊩^z Θ.

Finally, Proposition 3.6 shows that ∧R↓ is not correct for ⊩^B. But it is correct for ⊩^z. To see this, suppose that Σ⊩^z Θ,A and Σ⊩^z Θ,B. That is, neither ⌊Σ:Θ,A⌋ nor ⌊Σ:Θ,B⌋ shadows the empty position. So either: the empty position implicitly asserts some θ∈Θ, or it implicitly denies some σ∈Σ, or it implicitly asserts both A and B. In either of the first two cases, ⌊Σ:Θ,A∧B⌋ does not shadow the empty position for the same reason. In the third case, the empty position must also implicitly assert A∧B, ¹¹ and so again ⌊Σ:Θ,A∧B⌋ does not shadow it. Either way, then, Σ⊩^z Θ,A∧B.

So I definitely agree with French’s claim that ‘[if ⊩^B] has a story to tell about when, for example, tolerant denial of a conjunction is out of bounds it cannot be the standard story.’ But ⊩^z does not seem to be so limited. I think, then, that there is nothing in French’s idea of umbral positions or shadowing that results in nonstandard approaches to the connectives. It’s just that the standard approaches appear in the relation ⊩^z, not (or not fully) in the relation ⊩^B.

Strong Kleene models

First, the understanding in terms of strong Kleene models. Szmuc calls this ‘a non-transitive subsystem of’ the system P_S, where P_S is defined just like ST^c except for using ^two-valued classical models instead of strong Kleene models. I think it’s worth highlighting here Szmuc’s footnote 15, and expanding on it a bit.

The main topic of that footnote has to do with what it takes to be ‘non-transitive.’ Unfortunately, that issue is seriously clouded by wild variations in terminology from author to author. To try to sort it out would be a bigger project than I can do here. ¹² So I’ll leave that issue to one side. The footnote does, however, highlight the importance of being precise about what vocabulary is present in the language before making claims about systems like ST^c, and that’s what I want to focus on. This matters in particular here for getting clear on the relationship between ST^c and P_S.

If we work in an ordinary propositional or first-order language, ST^c and P_S validate exactly the same sequents as each other. The reasoning is just as for the systems Szmuc calls ST and CL; see for example Ripley (²⁰¹², Lemma 2.8) for that. So while it’s true in this case that ST^c is a subsystem of P_S, it’s perhaps misleading to say it that way without further comment; it’s just as true that P_S is a subsystem of ST^c.

On the other hand, if we add a transparent truth predicate to the language, P_S becomes the empty logic: as there are no classical models at all with a transparent truth predicate, owing to the paradoxes, the conditions that must obtain for P_S validity are never met. ST^c does not collapse in this way. So in this case, it’s not true that ST^c is a subsystem of P_S at all; it’s rather the other way around.

The bounds

Whether we understand ST^c in terms of strong Kleene models or in terms of the bounds, it treats premises and conclusions very differently from each other. For example, working with the strong-Kleene-model understanding, we have p⊢_STc p,q but ¬p,p⊬_STc q. Both cases are cases where we cannot assign all the premises value 1 and all the conclusions value 0. But in the former case, the reason why has to do with a premise and a conclusion, while in the latter case, the reason has to do with two premises. STc is sensitive to this difference: basically, when the reason has to do with two premises (or two conclusions), it gets special treatment.

We can see a similar phenomenon working with the bounds understanding. Let me use a first-order language to represent English, with the predicate B for ‘is bigger than,’ and the names m,c,d for ‘Melbourne,’ ‘Canberra,’ ‘Darwin,’ respectively. Then we have Bmc,Bcd⊢_STc Bmd. But we do not have Bmc,Bcd,¬Bmd⊢_ST ^c. In either case, the positions represented are out of bounds: it is out of bounds to assert Bmc and Bcd while denying Bmd; and it is also out of bounds to assert all of Bmc,Bcd, and ¬Bmd. But because the latter case involves assertion only, ST^c treats it differently from the former, which involves both assertion and denial.

That is, ST^c on either understanding cares a great deal about the difference between having a claim as a conclusion and having the negation of that claim as a premise. The same kinds of differences obtain between having a claim as a premise and having its negation as a conclusion.

If we’re working with strong Kleene models, I see no problem here; we’re free to set up whatever kind of formal system we like, and this is a perfectly good one! But once we’re interpreting these systems as telling us something about our conversational practices, I start to worry a bit about this phenomenon. In terms of the bounds, ST_c is sensitive to the difference between a claim’s being denied and its negation being asserted, and likewise between a claim’s being asserted and its negation being denied.

When it comes to actually recognizing speech acts, however, it can sometimes be difficult to tell the difference between a denial of A and an assertion of ¬A, or between an assertion of A and a denial of ¬A. Indeed, some have claimed that these are the very same acts: that every denial of A is at the same time an assertion of ¬A, and that every assertion of A is at the same time a denial of ¬A. ¹³

Let’s suppose for a moment that that’s right. Then ST^c’s treating assertions so separately from denials would seem unmotivated. But there is a relation in the area that might be more natural, suggested by Szmuc’s remarks about ‘relevant assertion’ and ‘relevant denial.’ Say that position is tight iff it’s out of bounds and all its proper subpositions are in bounds. Then a tight position is one in which every assertion and every denial is relevant, in Szmuc’s sense. For example, the position containing assertions of ‘Melbourne is bigger than Canberra’ an ‘Canberra is bigger than Darwin’ and a denial of ‘Melbourne is bigger than Darwin’ is a tight position; it’s out of bounds, but removing any one of these acts leaves a position that’s in bounds.

Now, say that Γ⊢_STt Δ iff the position [Γ⇒Δ] is tight. ST^t seems to fit better with the motivations Szmuc gives than ST^c does. In particular, as long as the bounds do not distinguish between an assertion of ¬A and a denial of A, then ST^t will not either. In this regard, it’s unlike ST^c. However, it seems to sit better with Szmuc’s motivation in terms of relevant assertions and denials than ST^c does.

A question

The issue is this: there’s clearly something nonclassical about logical approaches to vagueness and truth like those I explore in Uncut. At the very least, that’s an initial response that a number of people have had to these approaches, and one that I think is worth understanding. But how can we understand it precisely?

Again, it’s important not to get caught in false controversies: the question here isn’t about what really counts as a classical theory of vagueness or truth. That’s a pure terminological question, which everyone is free to settle by stipulation as they choose. Rather, the question here is about diagnosing a certain kind of informed but inarticulate intuition: is there an interesting distinction that these intuitions are tracking?

There is of course an obvious sense of ‘nonclassical’ available, call it ‘nonclassical₁’: a logical system is nonclassical1 iff it fails to validate some classically-valid argument. This can’t be a way of understanding the feeling of nonclassicality, though, since the nontransitive systems in question are all classical1.

In Cobreros et al. (²⁰¹³) and Ripley (²⁰¹³), my collaborators and I began to articulate a different way to see these systems as nonclassical, based on metainferences. While the validities of these systems are closed under many of the same metainferences as validity in classical logic, they do not match perfectly. Most notably, of course, validity in classical logic is closed under the metainference cut, unlike validity in nontransitive systems. So this gives us a second sense, call it ‘nonclassical₂’: a logical system is nonclassical2 iff it fails to be closed under some classical metainference, where a classical metainference is a metainference obeyed by pure classical logic. Owing to the failure of cut (among many others), the nontransitive systems in question are certainly nonclassical₂.

The trouble with understanding nonclassicality in this way, as we point out in Cobreros et al. (²⁰¹³), is that every nontrivial extension of classical logic fails to obey some metainference obeyed by classical logic itself. So sure, nontransitive theories of truth are nonclassical₂, but so is classical Peano arithmetic. ¹⁴ This too, then, fails to articulate the feeling.

Still, it seemed that metainferences matter somehow. So given a set Σ of metainferences obeyed by classical logic, let a logical system be classical_Σ iff it obeys every metainference in Σ. Now we’ve got uncountably many distinct notions of classicality. This might help us precisely articulate all kinds of things, but it still doesn’t answer the initial question: what’s driving the robust intuition of nonclassicality here? Any choice of a particular Σ seems arbitrary.

The answer, I now think, is in Teijeiro’s paper, and in particular in Fact 4.1. (The answer is probably also implicit in Barrio, Rosenblatt, & Tajer (²⁰¹⁵), but I see that only with hindsight.) It is the schematic metainferences that provide a particularly relevant choice of Σ.