1. INTRODUCCIÓN
Este trabajo es la primera etapa de una investigación realizada en el marco de una tesis de maestría en enseñanza de ciencias exactas y naturales de la facultad de ingeniería de la Universidad Nacional del Comahue, y que tiene como finalidad la elaboración de un modelo epistemológico de referencia (MER) alternativo para el estudio de la divisibilidad sobre el conjunto de los números enteros.
Como primer paso intentaremos caracterizar el modelo epistemológico dominante (MED) de la divisibilidad presente en la escuela secundaria de nuestra región y, dialécticamente necesaria, en la formación de profesores. Para esto comenzaremos con una exploración de libros de textos de secundaria y de los últimos años de la escuela primaria, a fin de recabar información que nos permita caracterizar las organizaciones matemáticas (OM) presentes, las relaciones entre ellas y las prácticas matemáticas asociadas a las mismas que se privilegian en la escuela secundaria en nuestra región.
Para llevar a cabo la exploración en los libros de texto se formularon cinco conjeturas que permiten analizar el grado de completitud de las OM propuestas (Fonseca, 2004; Lucas, 2010) y por cada conjetura, una específica para las OM involucradas con la divisibilidad.
Las OM consideradas son las construidas en torno a:
- búsqueda de múltiplos y divisores.
- cálculo del máximo común divisor (MCD) y mínimo común múltiplo (MCM).
- uso de los criterios de divisibilidad.
- aplicaciones del algoritmo de la división y del teorema fundamental de la aritmética (TFA).
Estas OM se eligieron en función de lo establecido por los diseños curriculares de Neuquén (Ministerio de educación provincia de Neuquén. Resolución N°1463/18), Río Negro (Ministerio de educación y derechos humanos Río Negro. Resolución N°945/17) y los núcleos de aprendizajes prioritarios (NAP) (Ministerio de Educación, Ciencia y Tecnología. Resolución N°225/04) del sistema educativo argentino. Si bien el TFA no aparece explícitamente en las currículas oficiales, consideramos oportuno su incorporación puesto que proporciona un elemento tecnológico-teórico imprescindible y algunas de las técnicas presentadas en los libros de texto analizados hacen un uso implícito de este resultado, como se verá más adelante.
2. MARCO TEÓRICO
Para realizar nuestro análisis, nos posicionamos desde la perspectiva teórica que nos brinda el marco de la teoría antropológica de lo didáctico (TAD) (Chevallard, Bosch y Gascón, 1997, Chevallard 1999, 2007, 2013). Para analizar la actividad matemática institucionalizada, la TAD propone un modelo epistemológico general de las actividades humanas en general, y de la actividad matemática en particular, que permite describir a las mismas en términos de praxeologías (Chevallard 1999). La noción de praxeología permite considerar al mismo tiempo y, atribuyéndole importancia equivalente, tanto la dimensión teórica como la dimensión práctica del saber. Una praxeología designa la unión de un bloque práctico- técnico que describe el saber hacer, formado de un tipo de tareas T y de al menos una técnica disponible τ para resolver las tareas del tipo T, con un bloque tecnológico-teórico, que explicita y describe el saber propiamente dicho, constituido de una tecnología θ que justifique, explica y hace inteligible a la técnica τ y de una teoría Φ que brinda el marco justificativo de la tecnología θ, mediante el cual, esta última construye su discurso.
De manera más explícita decimos que, como toda obra humana, una organización matemática (en adelante OM) surge como respuesta a un conjunto de cuestiones y como medio para llevar a cabo, en el seno de cierta institución, determinadas tareas problemáticas.
Las tareas problemáticas o cuestiones asociadas a una OM acaban cristalizando en uno o más tipo de problemas, generados por el desarrollo de la actividad matemática del estudio de las cuestiones iniciales. En general, podemos decir que si un tipo de problemas es considerado en cierta institución es porque en la institución existe al menos una técnica matemática que permite, no sólo resolver estos problemas, sino también generar muchos más del mismo tipo (Lucas, 2010).
Las OM más elementales se llaman puntuales y están constituidas alrededor de lo que en determinada institución es considerado como un único tipo de tareas. Cuando una OM se obtiene por integración de cierto conjunto de OM puntuales, tales que todas ellas aceptan un mismo discurso tecnológico θ, diremos que tenemos una OM local caracterizada por dicha tecnología θ.
Una OM local permite plantear y resolver problemas (o, al menos, responder ante ellos) que en las OM puntuales iniciales no podían formularse con toda propiedad. Resulta, por tanto, que estas nuevas cuestiones problemáticas deberían constituir la “razón de ser” que dan sentido a la OM local (Chevallard, 1999). Aunque en la TAD se habla también de OM “regionales” y “globales”, en este trabajo no iremos más allá del análisis de una OM “local” que vive en la Enseñanza Secundaria: la que se estructura en torno a la divisibilidad.
En la TAD, los procesos de modelización se entienden como procesos de reconstrucción y articulación de organizaciones matemáticas de complejidad creciente, que deben partir de las razones de ser de las organizaciones matemáticas que se quieren construir.
En diversas investigaciones se pone de manifiesto una extraordinaria rigidez en la enseñanza secundaria de las matemáticas. Se plantea que los alumnos tienen problemas con la nomenclatura, manejan una sola técnica, no son capaces de distinguir entre tarea directa y tarea inversa, no interpretan las técnicas y, lo que es más importante, tienen una extraordinaria dificultad para trabajar con tareas abiertas. Todo ello provoca una incompletitud de la actividad matemática desarrollada y una desarticulación de las matemáticas escolares (Fonseca, 2004; Lucas 2010).
Para salvar los obstáculos que este fenómeno de rigidez y desarticulación de las OM presentan en las instituciones escolares, desde la TAD se han caracterizado algunos indicadores que permiten medir el grado de completitud relativa de las OM que viven en una institución. Es así como surge la noción de organizaciones matemáticas locales relativamente completas (OMLRC)”, que permite describir y analizar el grado de completitud de una OM propuesta en el seno de una institución (Fonseca, 2004). Hay que subrayar, que la noción de “completitud” es relativa. No tiene sentido hablar de OML “completas” ni de OML “incompletas”. Se trata, en todo caso, de una cuestión de grado: existen OML más o menos “completas” que otras en función del grado en que sus componentes cumplen las condiciones descritas por los indicadores. En este trabajo nos guiaremos de los indicadores referidos por Cecilio Fonseca, (2004), y Catarina Lucas (2010) para medir el grado de completitud de una organización matemática local.
Para poder estudiar un ámbito matemático dentro de la TAD es necesario describir y dar una interpretación de lo que, como investigadores, vamos a considerar dentro de ese ámbito matemático y que constituirá el modelo epistemológico de referencia (MER). La elaboración de ese MER es el primer paso necesario para construir el problema de investigación, y no constituye un modelo en el sentido normativo del término, sino que es una herramienta del trabajo teórico-experimental y, como tal, es siempre provisional, permanentemente puesto a prueba a partir de su contraste con la realidad que se investiga. Su explicitación forma parte de la dimensión epistemológica de los procesos de investigación y es considerada fundamental (Gascón, 2011).
Para el análisis de la dimensión económica del problema didáctico, es decir, de las cuestiones relativas al sistema de reglas y principios que regulan la organización y el funcionamiento, en la institución, de las praxeologias matemáticas y didácticas involucradas, es necesario explicitar el modelo epistemológico dominante (MED), a menudo implícito, que se “impone” a los sujetos de la institución y que tiene una importancia didáctica crucial, puesto que determina lo que se entiende en torno al objeto matemático en cuestión y lo que se entiende por “enseñar y aprender matemáticas” dentro de dicha institución. Además, el MED de cierto ámbito del saber matemático enseñado (en una institución determinada) condiciona fuertemente no sólo el tipo de actividades matemáticas que será posible llevar a cabo en dicha institución en torno al ámbito matemático en cuestión, sino también las correspondientes actividades didácticas que se materializan en un modelo docente. En consecuencia, la emancipación epistemológica comporta, en cierta medida, la emancipación respecto del MED en la institución, lo que proporciona autonomía para cuestionarlo y para proponer otros modelos docentes alternativos.
3. METOLOGÍA
Como dijimos anteriormente, para caracterizar el MED de la divisibilidad en la escuela secundaria comenzaremos con el análisis de libros de textos escolares.
3.1. Elección de los libros de texto
Inicialmente, para establecer en qué años del nivel secundario de nuestra región se estudia explícitamente la divisibilidad, procuramos efectuar un abordaje de los programas oficiales del nivel secundario, en particular analizamos los núcleos de aprendizaje prioritarios dispuestos por nación, y los diseños curriculares de Río Negro y Neuquén. Una vez establecidos los cursos en los que se propone estudiar divisibilidad pasamos a la elección de libros de texto. Los libros utilizados para el estudio de las características de las OM en torno a la divisibilidad fueron elegidos y clasificados teniendo en cuenta dos categorías:
- Los libros de tipo A: son libros utilizados frecuentemente en las escuelas de Río Negro y Neuquén según análisis de programas anuales cedidos por los docentes, encuesta realizada a docentes y a las principales librerías sobre los libros más vendidos en los últimos dos años.
-Los libros de tipo B: son incluidos en este análisis debido a que sus autores y coordinadores de edición tienen una amplia trayectoria y reconocimiento a nivel nacional en Didáctica de la Matemática. Además, son libros calificados positivamente por el grupo de investigación dada su propuesta didáctica y su adecuación a los NAP.
La siguiente tabla (Tabla 1) muestra los libros organizados por las categorías mencionadas y por la etapa educativa a la que corresponden, 7° grado correspondiente al último año de la escuela primaria y 1° y 2° de la escuela secundaria.
Tabla 1: Libros de textos de nivel primario y secundarios utilizados para el análisis.
A modo general observamos que los libros del tipo A de 1° y 2° año destinan una sección del capítulo de números naturales (o enteros) al tema a estudiar (la divisibilidad). En cambio, el libro de 7° destina todo un capítulo al estudio de múltiplos y divisores. Sin embargo, la estructura de 7° a 2° año se repite, presentando la definición de múltiplo y divisor, una lista con los criterios de divisibilidad, definición de números compuestos y primos, factoreo y por último cómo utilizar la técnica de factoreo para la búsqueda del MCD y el MCM. Continuo a cada presentación se detallan una serie de ejercicios en su mayoría de aplicación de las técnicas mencionadas. En cambio, la estructura de los libros del tipo B destinan un capítulo completo al tema múltiplos y divisores y, comienzan en cada uno con una serie de problemas para introducir el tema y recuperar organizaciones matemáticas estudiadas en años anteriores. Cabe destacar que el foco gira en torno a los problemas y al finalizar un conjunto de problemas se institucionalizan algunas definiciones o se pone a la luz la variedad de técnicas que fueron utilizadas durante el desarrollo de las actividades.
3.2. Indicadores para el análisis del grado de completitud de la OM.
Para comenzar nuestro análisis vamos a postular la siguiente hipótesis de trabajo: Las OM presentes en los libros de texto en torno a la divisibilidad de números enteros presentan un alto grado de incompletitud relativa.
A fin de comprobar esto, se consideran las siguientes conjeturas que resultan de la negación de las características de los indicadores del grado de completitud (o incompletitud) de una OM propuestos por Cecilio Fonseca (2004) y Catarina Lucas (2010), que permiten construir una OMLRC.
C1: Las tareas no permiten explorar la potencialidad y el real funcionamiento matemático de las técnicas.
C2: La aplicación de una técnica para resolver una tarea no implica la interpretación del resultado.
C3. A cada tarea está asociada una técnica privilegiada.
C4: No hay reversión de las técnicas para realizar la tarea “inversa”
C5: No hay situaciones abiertas de modelización
4. DESARROLLO Y ANÁLISIS
A partir de las conjeturas mencionadas anteriormente, analizamos los libros de textos, lo que nos permitió llegar a las conclusiones que se detallan a continuación.
C1: Las tareas no permiten explorar la potencialidad y el real funcionamiento matemático de las técnicas.
En particular para el análisis de esta conjetura se buscaron tareas relacionadas a las siguientes técnicas:
- Uso de los Criterios de divisibilidad
- Uso del Algoritmo de la división
- Descomposición en factores primos (TFA)
Se tratará de dar respuesta a las siguientes preguntas (Tabla 2):
Tabla 2: Preguntas relacionadas a la conjetura 1
| C11 | ¿Qué tipo de tareas permiten reflexionar sobre la potencialidad del uso de los criterios de divisibilidad, más allá de su mera aplicación? |
| C12 | ¿Qué tipos de tareas permiten reflexionar sobre la pertinencia y potencialidad del uso del algoritmo de la división? |
| C13 | ¿Qué tipo de tareas permiten reflexionar sobre la pertinencia, potencialidad y economía del TFA? |
Conclusión 1: En los libros de tipo A podemos decir que no encontramos tareas que permitan reflexionar sobre la potencialidad de las técnicas analizadas según C11, C12 y C13. En estos libros, podemos asegurar que el trabajo gira en torno a la aplicación de las técnicas, sin ningún tipo de cuestionamiento sobre su uso. Además, tampoco se reconoce la presencia de la tecnología que las explica y justifica. A modo de ejemplificar C11, presentamos los criterios de divisibilidad enunciados al inicio del capítulo en uno de los libros del tipo A (Figura 1):
A continuación, mostramos una actividad extraída de uno de los libros del tipo A (Figura 2), en la cual se espera únicamente la aplicación directa de los criterios antes mencionados (Figura 1), sin necesidad de un análisis previo.
Observamos que para completar el inciso “a” solo basta con agregar un número de forma tal que “la suma sucesiva de sus cifras sea 3,6 o 9” lo cual no permite ver la ventaja de un criterio sobre otro, es decir imposibilita la selección propia del criterio más pertinente. Además, este tipo de tareas no permite el uso de otro tipo de técnicas que puedan contrastarse con los criterios de divisibilidad.
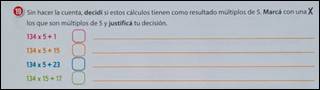
En cambio, en los libros del tipo B, respecto a C11, se observa un trabajo genuino para establecer algunos criterios de divisibilidad. A modo de ejemplo se presenta la siguiente actividad (Figura 3) donde se analiza si un número expresado como “calculo” es múltiplo de 5. Observamos que el primer término de las expresiones se corresponde con múltiplos de 5 y basta analizar qué ocurre con el segundo término para establecer si son múltiplos de 5 o no.
Cabe mencionar que este tipo de tarea fomenta la construcción de una nueva técnica que involucra la descomposición en sumas y productos para establecer si se trata de un múltiplo y descentraliza como única técnica el criterio de divisibilidad por 5.
Siguiendo la misma línea, la siguiente actividad (Figura 4) propicia establecer condiciones similares, pero para el número 3.
Es así que, en búsqueda de afianzar y constituir una regla, el tipo de actividad propuesta se despoja de la expresión aritmética (descomposición en sumas y multiplicaciones) como muestra la siguiente actividad (Figura 5) y trata de buscar generalizaciones en un lenguaje coloquial con dos pares de números naturales.
Es por esto que podemos decir que, en este tipo de libros, el trabajo se centra en la descomposición en sumas y multiplicaciones de un número, las cuales permiten comprender cómo surgen los criterios aportando una nueva técnica que resulta útil para cualquier número en general y no sólo para unos pocos.
En cuanto a C12, en los libros del tipo A para 7° y 1° año, aparece definido el algoritmo de la división en el capítulo de números naturales, en cambio en 2° año únicamente se define la división para números enteros en forma conjunta con la regla de los signos. En el caso de 7° se define el algoritmo de la división, y se detalla: “Cuando el resto de una división entera es 0 (cero), la división es exacta” (P. Effenberger, 2013, p 10). Esta definición es retomada en el capítulo siguiente de Múltiplos y Divisores: “un divisor es un número que divide exactamente a otro” (P. Effenberger, 2013, p 28). Dada esta salvedad no se vuelve a utilizar el algoritmo de la división, salvo en algunos cálculos aritméticos.
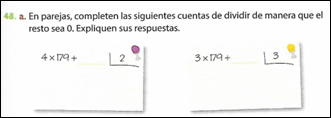
En cambio, la siguiente actividad (Figura 6) correspondiente a un libro del tipo B, muestra un tipo de tarea muy frecuente en estos libros con respecto a C12. La misma consiste en analizar, sin hacer la cuenta, si una expresión compuesta por sumas y multiplicaciones tiene resto cero al dividirla por un número dado.
Podemos decir que las tareas de este tipo (Figura 6) permiten poner en funcionamiento el algoritmo de la división en diferentes sentidos: como técnica para determinar si un número es divisor (múltiplo) de otro, como algoritmo de la división propiamente dicho, determinando divisor, dividendo, cociente y resto, como modelo algebraico introduciendo la letra como variable, entre otros. Destacamos que este tipo de tareas lleva a establecer estrechas conexiones entre el algoritmo de la división, las expresiones equivalentes y la letra como variables a partir de un contexto envuelto en la divisibilidad. Habitualmente, en la escuela, son temas abordados en forma individual y aislada, dejando en manos del estudiante la tarea de relacionarlos entre sí de manera espontánea.
En cuanto a C13, en los libros del tipo A primero define número primo, luego número compuesto y continuo hace una referencia de la unicidad de los factores primos de los números compuestos, como muestra la siguiente imagen (Figura 7):

Recuperado de Abálsamo R. et al. Matemática 1, 2013. pág 21.
Figura 7: Definición de número primo y número compuesto en libro de tipo A.
Es así que damos cuenta que “menciona” el TFA, sin embargo, a partir de las tareas analizadas podemos decir que el objetivo no es la reflexión sobre su pertinencia y economía, sino que las mismas apuntan a una mera aplicación repetitiva de la factorización en factores primos para encontrar MCM (MCD) o simplemente descomponer un número en sus factores primos sin una auténtica necesidad. Esto último se ampliará en el desarrollo de C3.
Así mismo, en los libros del tipo B, podemos decir que tampoco se observa un trabajo profundo en torno al TFA. En la serie de libros del tipo B analizados se puede observar que los tipos de tareas aportan un camino apropiado para el análisis de propiedades de los números desde la descomposición en sumas y multiplicaciones en el campo de los naturales. Además, se amplía estas nociones y técnicas al conjunto de los números enteros, para luego continuarlo hacia un trabajo algebraico, apoyándose en los conocimientos sobre números y operaciones. En esta propuesta, algo que observamos es que estas técnicas, definiciones y propiedades se presentan despojadas de sus razones de ser. En ningún momento aparece la necesidad de descomponer estos números aditivamente o multiplicativamente a partir de una situación que lo demande, más allá de saber si un número es múltiplo de otro o no. Es por esto que podemos decir que en los libros del tipo A y B no se observan tareas específicas que permitan reflexionar sobre la pertinencia, potencialidad y economía del TFA. Así también, en ambos casos, se observó que la descomposición en factores primos queda subordinada al uso de números primos de una cifra como podemos observar en las actividades que se muestran (Figura 8 - Figura 9):

Recuperado de Abálsamo R. et al. Matemática 1, 2013. pág 22
Figura 8: ejemplo de C13 en libro de tipo A.
En el caso de la Figura 8, los números primos que aparecen involucrados en la descomposición son los siguientes:
792=2.2.2.3.3.11
600=2.2.2.3.5.5
1089=3.3.11.11
4410=2.3.3.5.7.7
Y en la Figura 9 son:
42x18= 2.2.3.3.3.7
28x90= 2.2.2.3.3.5.7
21x65= 3.7.5.7
En la serie de libros del tipo B, aparecen los números primos 19 y 37 como los más grandes. A partir del tipo de tarea descripto, podemos decir que ambos libros fomentan una posible conjetura errónea: que los números primos son únicamente números pequeños que no van más allá de 2,3,5,7 y 11. Tampoco se identificaron tareas que permitan reflexionar sobre la existencia y unicidad de la descomposición.
C2: La aplicación de una técnica para resolver una tarea no implica la interpretación del resultado.
Las tareas analizadas en este punto se agruparon en tres tipos de tareas:
- Calcular los múltiplos (o divisores) de un número natural.
- Calcular el MCM (o el MCD) de dos números naturales.
- Determinar si un número natural es múltiplo de (o divisible por) otro número natural.
En particular para analizar esta conjetura se tratará de dar respuesta a las siguientes preguntas (Tabla 3):
Tabla 3 Preguntas relacionadas a la conjetura 2
| C21 | ¿Qué tareas respecto al cálculo de múltiplos (divisores) de un número incluyen la interpretación del resultado? |
| C22 | ¿Qué tareas respecto al cálculo del MCD (MCM) incluyen la interpretación del resultado? |
| C23 | ¿Qué tareas para determinar la divisibilidad de un número por otro incluyen la interpretación del resultado? |
Conclusión 2: De manera global podemos decir, a partir del análisis de las preguntas C21, C22 y C33 con respecto a nuestra conjetura C2, que existe una brecha notoria entre las tareas y la interpretación de sus resultados comparando los libros del tipo A y los del tipo B. Además podemos decir que ambos libros muestran cierto grado de incompletitud relativa que los hace perfectibles.
Por un lado, los libros de tipo A conciben la tarea como una mera aplicación de la técnica presentada, sin la necesidad de interpretar los resultados, pues el foco está puesto en “saber aplicar”. A modo de ejemplo la siguiente actividad (Figura 10) resulta representativa del tipo de tareas propuestas en estos libros.

Recuperado de Abálsamo R. et al. Matemática 1, 2013. pág 24
Figura 10: ejemplo de C22 en libro de tipo A.
En los libros del tipo A, en general no queda determinado que deban ser justificadas las respuestas, es así que las actividades relacionadas al cálculo de MCM (MCD) quedan limitadas únicamente al tipo de tareas mostrada (Figura 10). Estas tareas refuerzan la “irresponsabilidad matemática” de los estudiantes (Chevallard et al., 1997, p.77) pues no permiten reflexionar sobre la aplicación de las técnicas y dejan en manos exclusivamente de otros la validación y evaluación del éxito de las mismas.
Por otro lado, y contrariamente, en los libros del tipo B las tareas invitan a la exploración, validación y justificación, y en consecuencia a una necesaria interpretación de los resultados obtenidos. A modo de ejemplo podemos citar los ejemplos de las figuras 3,4,5 y 6 mostradas anteriormente y agregamos las siguientes actividades (Figura 11):
Consideramos pertinente mencionar esta actividad (Figura 11) ya que detectamos que, en los libros analizados correspondientes a 1° y 2° año, no se busca construir directamente los criterios como se hizo en el libro de 7°, pero si se retoman tareas similares a las de 7°, utilizando los criterios de divisibilidad y fuertemente la descomposición en sumas y productos como medio para incorporar la letra como variable. Lo cual nos lleva a reafirmar que el foco está puesto en un trabajo de exploración, validación y justificación arraigado fuertemente a la interpretación de los resultados.
C3. A cada tarea está asociada una técnica privilegiada. Para analizar esta conjetura se consideraron las mismas tareas que en la conjetura anterior. En particular se tratará de dar respuesta a las siguientes preguntas (Tabla 4):
Tabla 4: Preguntas relacionadas a la conjetura 3.
| C31 | ¿Qué técnicas se proponen vinculadas a la búsqueda de múltiplos (divisores)? |
| C32 | ¿Qué técnicas se proponen en la búsqueda del MCD y MCM? |
| C33 | ¿Qué técnicas se proponen para determinar la divisibilidad de un número por otro? |
Conclusión 3: Con respecto a la pregunta C31, en los libros del tipo A la técnica que se desprende de la definición dada de múltiplo es que un número natural a es múltiplo de un número b si se puede expresar al primero como producto del segundo por otro número natural. En el caso del divisor la técnica asociada es dividir ambos números y si la división es exacta, uno es divisible por el otro. Además, en estos libros se institucionaliza cómo encontrar todos los divisores de un número natural haciendo las combinaciones posibles entre los números primos que resultan de su factorización como muestra la siguiente figura (Figura 12).
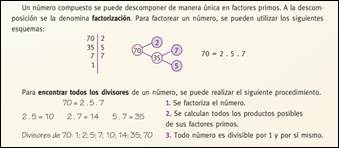
Recuperado de Abálsamo R. et al. Matemática 1, 2013. pág 21
Figura 12: ejemplo de C31 en libro de tipo A.
En el caso de los libros del tipo B, se puede observar que las técnicas utilizadas son similares a la de los libros del tipo A, con la diferencia que las definiciones son institucionalizadas al finalizar tareas que involucran estas técnicas implícitamente. La siguiente figura (Figura 13) muestra la institucionalización que da el libro al finalizar con un tipo de tareas que inducen directamente a esta formalización.
Al analizar la pregunta C32, pudimos observar que en el caso de los libros del tipo A, la tarea de calcular el MCM (o el MCD) se vincula estrechamente con una única técnica, la descomposición en factores primos con la ayuda de una tabla como muestra la siguiente figura (Figura 14):

Recuperado de Abálsamo R. et al. Matemática 1, 2013. pág 23.
Figura 14: ejemplo de C32 en libro de tipo A.
Como se observa en la figura 14, inicialmente se listan los primeros siete múltiplos positivos de cada número y se marcan los múltiplos en común, eligiendo como el MCM al menor de ellos. Luego se presenta la técnica experta: “para calcular el mcm se multiplican los factores comunes y no comunes con su mayor exponente”
De manera análoga presentan la técnica predilecta para la búsqueda del MCD entre dos números dados, como muestra la siguiente figura (Figura 15):

Recuperado de Abálsamo R. et al. 1 Matemática, 2013. pág 23.
Figura 15: ejemplo de C32 en libro de tipo A.
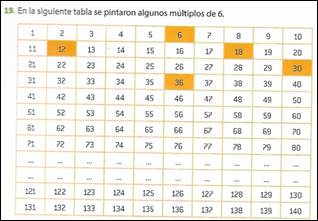
En cambio, en los del tipo B se fomenta un trabajo exploratorio sin definir específicamente una técnica como válida o superadora al resto. La actividad que se muestra a continuación (Figura 16 y Figura 17) extraída del libro de 1° año de esta serie de libros, analizamos que recupera la noción de múltiplo ya abordada en 7° grado e invita a la exploración y pone a la luz diferentes estrategias para encontrar un múltiplo de 6 sobre la grilla numérica. Recupera no solo la definición de múltiplo, sino que también la noción de MCM a partir del tipo de tarea solicitada.
Cabe mencionar que el tipo de técnicas que emergen de las tareas son poco económicas para valores grandes. Además, la búsqueda de MCD y MCM es una tarea destinada a 7° grado y a 1° año, en 2° año no aparecen tareas relacionadas con esta búsqueda.
Con respecto a C33, en los libros del tipo A se detectaron dos técnicas, una es el uso del algoritmo de la división:
En el libro de 7° se define el algoritmo de la división, y se detalla: “Cuando el resto de una división entera es 0 (cero), la división es exacta”. (P. Effenberger, 2013, p 10). Esta definición es retomada en el capítulo siguiente de Múltiplos y Divisores: “un divisor es un número que divide exactamente a otro” (P. Effenberger, 2013, p 28). Otra técnica utilizada por los libros de esta categoría son los criterios de Divisibilidad, los cuales están definidos apenas comienza el capítulo como se mostró en la figura 1.
Según nuestro análisis, la técnica propuesta y predilecta por los libros de este tipo es el uso de los criterios de divisibilidad.
En cambio, los libros del tipo B direccionan su trabajo hacia la construcción, validación y justificación de los criterios de divisibilidad como se mostró anteriormente en C2 surgiendo los criterios mostrados en la Figura 13. Así mismo, cabe destacar cómo los libros del tipo B posibilitan la aparición de distintas estrategias relacionadas a C3 como, por ejemplo, la búsqueda de criterios de divisibilidad y la descomposición del número en sumas o productos más fáciles de analizar.
Luego de un análisis sobre los libros el tipo B con respecto a sus tareas, podemos asegurar que si bien no se presentan técnicas específicas para determinar cuándo un número dado es divisible por otro, todas las tareas apuntan a que emerjan en un principio los criterios de divisibilidad y luego la descomposición de un número en sumas y productos (Figura 3- Figura 4). Según nuestra lectura global de la serie de libros, la técnica de la descomposición en sumas y productos es la técnica predilecta y asociada directamente a la tarea de determinar si un número es divisible por otro. Podemos destacar, además, que existen otras técnicas asociadas a este tipo de tareas que no aparecen o no son propiciadas. Como, por ejemplo, el algoritmo de Euclides.
C4: No hay reversión de las técnicas para realizar la tarea “inversa”
Para analizar esta conjetura buscamos en los libros del tipo A y B la existencia de tareas inversas y uso de la reversión de la técnica sobre tipos de tareas que se vinculen a la búsqueda de MCM (MCD) de números enteros dados y a la tarea de determinar si un número entero es divisible por otro entero dado. En particular para analizar esta conjetura se tratará de dar respuesta a las siguientes preguntas (Tabla 5):
Tabla 5: Preguntas relacionadas a la conjetura 4.
| C41 | ¿Qué tipo de tareas demandan la inversión de las técnicas para hallar el MCD (MCM)? ¿Qué nivel de relación se establece entre la técnica para hallar el MCD (MCM) y su técnica inversa? |
| C42 | ¿Cuáles son las tareas que permiten la reversión de las técnicas utilizadas para determinar si un número natural es divisible por otro? ¿Qué nivel de relación se establece entre la técnica para determinar la divisibilidad de un número por otro y su técnica inversa? |
Conclusión 4: Podemos concluir con respecto a C41, que en ambos tipos de libros no son frecuentes las actividades que respondan al tipo de tarea inversa. En el caso de los libros del tipo A se puede observar que, si bien hay una tarea que potencialmente permitiría vincular un tipo de tarea con su inversa, como muestra la siguiente actividad (Figura 18), que consiste en hallar dos números naturales compuestos tales que su MCD (MCM) sea un número natural dado. Podemos observar que la consigna, por un lado, condiciona a que los números a hallar sean necesariamente compuestos y además no hace reflexión alguna sobre la inversibilidad de alguna de las técnicas para hallar el MCD y el MCM.
Consideramos que dado el contexto de las actividades y el momento en el que se presentan, son actividades destinadas a ser resueltas a partir del tanteo de valores, no requieren una justificación de la técnica aplicada ni la necesidad de determinar todos los valores que cumplen con las condiciones dada. Resaltamos la importancia de encontrar todos los valores, ya que esto permitiría un análisis profundo de la técnica y los elementos tecnológicos que la justifican.
En el caso de C42 utilizamos la siguiente identificación para referirnos a una tarea (T) y su tarea inversa (T-1)
T: dados a y b naturales, determinar si a es divisible por b (si b es divisor de a)
T-1: dados a y b naturales, determinar si a es múltiplo de b.
En el caso del análisis realizado con respecto a las tareas T y T-1 en los libros del tipo A y B, podemos decir que existen ambos tipos de tareas en diversos ejercicios y que además ambos tipos de libros proponen actividades que fomentan la relación que existe entre la noción de múltiplos y de divisores.
Sin embargo, en los libros del tipo A no se encontraron tareas que permitan establecer un nivel de relación entre la técnica sugerida para resolver T y T-1. Como mencionamos en C21 las técnicas para resolver este tipo de tareas son, el uso del algoritmo de la división, la descomposición en factores (como se mostró en la Figura 12) y el uso de los criterios de divisibilidad, considerando a esta última como técnica predilecta utilizada por este tipo de libros.
En cambio, en los libros del tipo B se reconoció una amplia variación de los tipos de tareas que permiten la reversión de las técnicas aplicadas. Considerando como técnica predilecta la que surge al tener en cuenta “si el resto de dividir a por b es cero, entonces b divide a a”, aparecen tareas que posibilitan abordar el formato del algoritmo de la división, pero analizando pequeñas variaciones en su dividendo o resto como muestra la siguiente imagen (figura 19):
También aparecen tareas que permiten relacionar el uso de la recta numérica con la ubicación de múltiplos y la lectura sobre el algoritmo de la división como muestran las actividades 27 y 28 en la siguiente imagen (Figura 20 y Figura 21):
Así también se logró poner a la luz la relación entre el algoritmo de la división y números expresados como productos o sumas de números naturales (enteros) como se muestra en las siguientes actividades (Figura 22):
C5: No hay situaciones abiertas de modelización.
En particular para analizar esta conjetura se tratará de dar respuesta a la siguiente pregunta (Tabla 6):
Tabla 6: Preguntas relacionadas a la conjetura 5
| C51 | ¿Qué situaciones “abiertas” se proponen que requieran un trabajo de modelización en torno a la divisibilidad? ¿Qué tareas abiertas se proponen que permitan establecer relaciones entre los diferentes objetos de la OM en torno a la divisibilidad? |
Conclusión 5: Si bien reconocemos la potencialidad de los problemas presentados en los libros del tipo B sobre los del tipo A, consideramos importante mencionar que los problemas presentados en ambos tipos de libros, en relación a la conjetura 5, son problemas cerrados, que aportan todos los datos necesarios para su resolución. No es necesario en estos problemas analizados seleccionar la información pertinente y tampoco la técnica necesaria pues en los problemas se observan incisos intermedios que guían hacia la técnica necesaria para su resolución. Cabe mencionar que este tipo de tareas cerradas no permite la toma de decisiones y autonomía en el trabajo matemático.
5. CONCLUSIONES
Luego del análisis de los indicadores planteados en los libros de textos seleccionados, podemos establecer que hay evidencia suficiente para afirmar que las organizaciones matemáticas propuestas para la escuela secundaria presentan un alto grado de incompletitud, especialmente en los libros del tipo A, que son los utilizados frecuentemente en las escuelas de Río Negro y Neuquén.
Con respecto al indicador dado por C1, observamos que en general, las tareas que se desarrollan en los libros de texto no permiten reflexionar sobre la potencialidad del uso de las técnicas. En los libros del tipo B hay unas pocas tareas relativas al cuestionamiento tecnológico, esto es, tareas cuya realización permita responder a cuestiones relativas a ciertas características de las técnicas matemáticas (dominio de validez, economía, justificación, interpretación de los resultados que se obtienen con ella, etcétera). Esto está totalmente ausente en los libros de tipo A.
El análisis de la conjetura C2 nos permite concluir que en el caso de los libros del tipo A, las tareas que se plantean no incentivan a que se realice una interpretación fehaciente de los resultados obtenidos al aplicar ciertas técnicas de resolución. Si bien en los libros del tipo B las tareas permiten realizar una exploración, validación y justificación de los resultados obtenidos, consideramos que sería mayor el nivel de completitud si contara con una mayor incidencia del bloque tecnológico-teórico.
La conjetura C3 hace evidente la rigidez de la OM analizada ya que en general hay una única técnica privilegiada asociada a cada tarea matemática. Si bien los libros del tipo A tienen más marcada esta rigidez, en ambos libros se termina haciendo énfasis en una de las técnicas, en el caso de los libros del tipo A en la descomposición en factores primos y en el uso de los criterios de divisibilidad, mientras que en los del tipo B la técnica es la descomposición en sumas y productos. Este aspecto limita a los estudiantes a que tengan la responsabilidad de decidir entre las diversas técnicas útiles para resolver una tarea, cuál es la más económica o la más fiable. Este fenómeno provoca la atomización de las diversas tareas, es decir, existe una asociación de una determinada técnica a cada tipo de tarea.
Acordando con Fonseca (2004), uno de los aspectos más importantes de la rigidez de las OMP que se estudian en la escuela secundaria se manifiesta en la no reversión de las técnicas matemáticas correspondientes. En términos del contrato didáctico podemos decir que no forma parte de la responsabilidad matemática del alumno invertir una técnica para llevar a cabo la tarea inversa. Del análisis que realizamos en los libros de texto a partir de la conjetura C4, podemos afirmar que en los libros del tipo A se observa ausencia de tareas inversas que permitan la exploración de la reversión de la técnica abiertamente, particularmente, cuando existen dos tareas inversas entre sí, las correspondientes técnicas suelen tratarse como si fueran independientes.
En el caso de los libros del tipo B, si bien se presentan algunas tareas donde es posible pensar en término de la reversibilidad de las técnicas, estas fueron tratadas como técnicas totalmente desvinculadas unas de otras. A lo largo de estos textos se busca hacer evolucionar las técnicas desde técnicas más elementales a técnicas más económicas y más robustas, pero no se trabaja la reversibilidad de las mismas.
Finalmente, del análisis de la conjetura C5, que según Fonseca (2004) es uno de los principales indicadores del grado de completitud de una OML, podemos afirmar que en ninguno de los libros analizados hemos observado existencia de tareas matemáticas “abiertas” que requieran un trabajo de modelización en torno a la divisibilidad. La importancia de este indicador de la completitud proviene del hecho de que la existencia de tareas abiertas presupone cierto grado de flexibilidad de las técnicas y, además, presupone que las OMP que constituyen la OML en cuestión han alcanzado cierto grado de articulación. No obstante, si bien reconocemos la potencialidad de los problemas presentados en los libros del tipo B, concluimos que la OM analizada no satisface completamente este indicador de completitud.