I. INTRODUCTION
We will start this article with a brief account of Poincaré's (Poincaré, 1912) work on Planck's quantum hypothesis, which is relevant to the theoretical foundation of Quantum Theory from statistical thermodynamics and the calcula-tion of probabilities. In this important article from the historical and mathematical physics point of view, Poincaré exposed, in an original way, the theoretical bases of the Planck equation for blackbody radiation, demonstrating in three different ways the necessity and sufficiency of the quantum hypothesis of action for radiation. At the end of the article, Poincaré stated that both mechanical collision processes and Döpler-Fizeau's law lead to the same energy-sharing law. Poincaré also promised to write a theory that would be able to include ether in the interaction processes between radiation and matter. This article published by Poincaré, will be discussed in a future publication.
Boltzmann had already published preliminary studies on this topic in the years 1866 (Boltzmann, 1968)and 1884 (L. Boltzmann, 1884), based on Maxwell's work in relation to the Kinetic Theory of Gases and the distribution of veloc-ities. Thomas Kuhn (Khun, 1978) considers these works fundamental for the further development of Quantum Theory. In this sense, Boltzmann is, when reinterpreting the laws of thermodynamics based on the notions of probability, statistics and entropy, one of the main theoretical contributors of Quantum Theory, as well as Poincaré (Khun, 1978), whose participation in the first Solvay Council in 1911 was fundamental to the developments later. We fully translated the 1912 Poincaré article and published it in the Doctoral Thesis (Rosa, 2019). Charles Galton Darwin published a commented English translation of Poincaré's article, which contributed to the acceptance of Planck's theory, since English scientists were more likely to accept Wien's theory.
Based on the Kinetic Theory of Gases, Boltzmann theoretically demonstrated the empirical law of Dulong-Petit (Laranjeiras, 2002) for ideal gases, but without using the Planck hypothesis, which appeared only in 1900. Einstein in 1907 (Einstein, 1906) when deducing an adjustment equation for the behavior of solid bodies, proved to be valid the notion of quantization of harmonic oscillators proposed by Planck.
In the next topic, we will address the conceptual character of the Dulong-Petit law, analyzing the original publica-tion (Dulong, Pierre L. y Petit, 1819) in French, as well as some controversial aspects about whether this law was conceived by both or if it belonged to François Arago (Fox, 1968). This law was discovered during a period when there was a fruitful debate about the corpuscular and undulating interpretation of the theory of heat (Brush, 1970).
II. THE DULONG-PETIT LAW AND THE CONTROVERSY WITH ARAGO
According to Fox (Fox, 1968), what the history of physics knows as Dulong-Petit's law, in fact, would have its origin in Arago's research. The 1881 account of French chemist Jean Baptiste Dumas (Dumas, 1881) (Dumas, 1883) seems to cast some doubt on the discovery of the law of specific heats for solid bodies.
Monday, April 5, 1819, a memorable date, Petit ... secretly showed his brother-in-law Arago a piece of paper, containing the reports of how the simple bodies combine, and the quantities of heat required for each to heat in the same way, having the same weight. At first, it seemed pure disorder, but when the two columns multiplied, all the products led to the same result. An hour later, the illustrious perpetual secretary, convinced that Dulong, always hesitant, could oppose the disclosure of this beautiful law, spoke of this to his colleagues, for a calculated indiscretion. Eight days later, the two collaborators announced themselves to the Academy... (Fox, 1968)
Fox omitted the passage in which Dumas comments about the misfortune of Petit's premature death, “..., dont un an plus tard la science déplorait la mort prémature...”. The correct page of Dumas's text would be xlviij, not xlviii, as it is in the footnote to Fox's article10. The publication date of the text also appears to be incorrect. Dumas's text was published by the French Academy of Sciences on March 14, 1881 (Dumas, 1881)and Fox quotes it as being published in 1883 (Dumas, 1883).
Perhaps Robert Fox's quotes are from publications after the original date. We are going to analyze Petit and Du-long's text on the specific heat for solid bodies from the historical point of view, as it is an important empirical law that does not appear in basic education textbooks and that in some way is associated with theoretical modification in basics and mechanical interpretation of natural phenomena.
Initially Petit and Dulong's 1819 (Dulong et al, 1819)article makes clear the need to obtain simpler laws for the composition of chemical compounds. These less complicated and more regular laws would be possible considering that the material properties would be linked to the actions of individual molecules. Petit and Dulong observed that Crawford and Irvine assumed that the amount of heat contained in the bodies would be proportional to their thermal capacity, thus, whenever the specific heat of the compound was very high or the average chemical composition of its elements, at the time of the combination, there would be absorption or release of heat.
According to Fox, all Dumas biographers claim that he came to Paris only in 1823, approximately three years after Petit's death, strongly suggesting that the account had its origin in Arago. Fox, doubts Dumas' account, considering that it is not correct in relation to the priority of the law. Due to Dumas` conflicting report, Fox decided to examine their publications in the years immediately preceding the discovery of the law (Fox, 1968). What can be concluded is that Arago, in fact, is acting as a defender and promoter of the Dulong-Petit law.
Petit and Dulong's article, Sur quelques points importants de la théorie de la chaleur, it can be considered histori-cal, since it describes the empirical construction of a fundamental law of physicochemistry: the microscopic behavior of atoms and molecules from the thermal point of view.
But, according to Petit and Dulong, the William Irvine and Adair Crawford hypothesis would be associated with the state of molecular aggregation. Crawford admitted that this hypothesis, based on his theory of animal heat (Crawford, 1788), is opposed to the observed facts, therefore, its application would be difficult. Even Dalton's hypothesis, accord-ing to which, the amount of heat of elementary particles, being the same in the elastic fluids, would have a difficult application, because, one would have to know the number of particles contained in the same weight or in the same volume in various gases.
In the 17th and 18th centuries, elastic fluids were interpreted by Boyle according to the idea of “spring of the air”. When introducing the mechanical basis of the air spring, Boyle compared the air to a ball of wool, which could be strongly compressed, but which would expand again if the compression force ceased (Rosa, 2019) (Brush, 1970). John B. West, made a detailed study of this interpretation based on the experiments carried out by Boyle (West, 2005). On the other hand, Hooke, Boyle's assistant at Oxford, admitted the concept of “springiness” (Centore, 1970). When, around the end of 1662, Hooke was struggling to determine the quantitative rarefaction of air under varying pressures, he used in addition to water, a certain amount of wine, “coarse spirit of wine”. The link between the works of physics in the 17th and 18th centuries and the process of construction of quantum theory lies in the fact that ether, a material substance present in the processes of mechanical interaction, has not been completely abandoned, despite the results of Michelson's experiments and Morley, show their nonexistence. Poincaré, still in 1912, discussed the possibility of building a mechanical theory with the presence of ether (Poincaré, 1912) (Gray, 2013).
Dulong and Petit rejected the theory proposed by Dalton because it presented only theoretical results, in addition to observing the inaccuracy of most measurements of physicists and chemists, except for those made by Laplace and Lavoisier, through their calorimeter, being very accurate, but in small amount. On the other hand, using the theory of elastic fluids, Delaroche and Bérard, (Jed Z. Buchwald, 2013) obtained expressive results for the calculation of specific heats in gases. J. L. Heilbron (Heilbron, 1993) describes in detail the experimental path of determining the specific heats of material bodies and experimental apparatus of various scientists, in determining this important constant in the thermal behavior of materials.
With the performance of these experiments, it was possible for Delaroche and Bérard to estimate, from expression (1), the specific heat at constant pressure for various substances, at a temperature of 0 0C and a pressure of 760 mmHg, by volume and by weight. Table 1, obtained by Delaroche and Bérard, shows some results of the experiment.
In this case, cp is the specific heat at constant pressure. The ratio ∆R/s∆T represents the gas flow per unit of time as a function of temperature variation. In this case, s is defined as the number of liters of gas passing through the calorimeter in the time unit and R is the temperature above the ambient air temperature.
Table I Specific heat at constant pressure.
| by volume | by weight | |
|---|---|---|
| air | 1.0000 | 1.0000 |
| hydrogen | 0.9033 | 12.3401 |
| carbonic acid | 1.2583 | 0.8280 |
| oxygen | 0.9765 | 0.8848 |
| nitrogen | 1.0000 | 1.0318 |
The empirical result for the specific heats in gases obtained by Delaroche and Bérard can be considered fundamental to explain the behavior of these fluid substances. Boltzmann, in 1866 (Boltzmann, 2012) obtained a mathematical expression that explained for the first time the behavior of gases from the determination of the number of atoms in the gas molecule.
Boltzmann defines p as the weight of the body “p das Gewicht des Körpers ist” - “p is the weight of the body” and “ist N die Anzahl der Atome im Körper” - “N is the number of atoms in the body”. To arrive at the specific heat equation (3), Boltzmann admits that if the oscillation time of the atom is equal to zero, that is,
Laranjeiras translates the conclusion of the topic “IV. Beweis des zweiten Hauptsatzes der mechanischen Wärme-theorie” - “Proof of the second law of the mechanical theory of heat” (Laranjeiras, 2002), stating that:
In this way, Boltzmann ends up establishing a theoretical proof of the Dulong-Petit law. Neumann’s law is an extension of Dulong-Petit’s law and states that the specific heat of a compound substance is the sum of the specific heat of its compo-nents. (Laranjeiras, 2002, p.93)
The analysis of Boltzmann’s deduction and the explanatory details in relation to formulas (2) and (3) can be verified in Laranjeiras (Laranjeiras, 2002). In equation (3), a represents the atomic mass or molecular mass, in the case of polyatomic molecules, and n represents the number of atoms of each molecule, with γ being the specific heat (Laranjeiras, 2002). Below, we put the passage translated by Laranjeiras.
Therefore, the product of specific heat by atomic mass is double that for the case of absolute gases at constant volume [“ideal gas”] where it is equal to 1. This law confirms what Masson had found for solids in an experimental path [see the aforementioned treaty “sur la correlation la... “[Sur la Correlation des Proprietés Physiques des Corps]”. Ann. de Chim., Ser.III, vol.53); (...). I will return, perhaps at another time, to the deduction of this formula for solid bodies, which seems, at the very least, to be the foundation of the approximate validity of Dulong and Petit’s law, or Neumann’s law. c]. (Laranjeiras, 2002, p.93)
Dulong and Petit showed that the empirical law for solid materials differs from the law presented for gases, alt-hough no theoretical demonstration to justify the law is seen in the 1819 (Fox, 1968) articles. According to the text, Dulong and Petit expressed the law as follows: “The atoms of all simple bodies have the same capacity for heat”. The table 2 shows the calculation for the simple compounds, produced through their experiments.
Table II Measurements of the specific heats of several simple bodies as a function of the relative weights of the atoms and the product of each atom by the corresponding thermal capacity.
| Specific heat (1) | Relative Weights of Atoms (2) | Products of the weights of each atom by the corresponding thermal capacity |
|---|---|---|
| Bismuth, 0,0288 | 13,30 | 0,3830 |
| Lead, 0,0293 | 12,95 | 0,3794 |
| Gold, 0,0298 | 12,43 | 0,3704 |
| Platinum 0,0314 | 11,16 | 0,3740 |
| Tin, 0,0514 | 7,35 | 0,3779 |
| Silver, 0,0557 | 6,75 | 0,3759 |
| Zinc, 0,0927 | 4,03 | 0,3736 |
| Tellurium, 0,0912 | 4,03 | 0,3675 |
| Copper, 0,0949 | 3,957 | 0,3755 |
| Níckel, 0,1035 | 3,69 | 0,3819 |
| Iron, 0,1100 | 3,392 | 0,3731 |
| Cobalt, 0,1498 | 2,46 | 0,3685 |
| Sulfur, 0,1880 | 2,011 | 0,3780 |
The original article shows the table but does not detail or outline the mechanism or apparatus with which both were able to determine these values. But we can see that by multiplying the 1st column by the 2nd, these products are constant. The table shows the number (1) in the first column and the number (2) in the second column, which in the original text refer respectively to: (1) La chaleur spécifique de l’eau est prise pour unite (The specific heat from the water is taken to the unit); (2) Les poids de l’atome d’oxigène est supposé égal à un (The weights of the oxygen atom are assumed to be equal to one). This means that Petit and Dulong determined the values of specific heats for some substances from their masses, taking as reference water, whose specific heat is 1.0 cal/g0C and oxygen, whose atomic weight is equal to 1. Therefore, the product of mass specific heat by relative atomic mass is exactly the specific heat per mol, regardless of the material. If we consider, for example, the specific heat value obtained for the lead in Table 2 we have: 0.0293 cal/g0C and compare it with the current value, around 0.031 cal/g0C, we find that the difference is of 0.0017, a very small error.
The most essential aspect of Dulong and Petit's Law is the universality of molar heat, both for solids and gases, when compared to specific mass heat. When observing the experimental results of the 1819 (Dulong et al, 1819) article’s, the important contribution of this law to the formulation of later mathematical models is verified. Because it is an empirically based law, it served as a support for testing atomic-molecular models.
According to Lewis (Lewis, 1907), these studies were fundamental for the establishment of consistent theoretical models in the relationships between pressure, volume and temperature.
The study of the relationship between the specific heat of gases at constant volume and constant pressure has led to a number of important theoretical conclusions, but in the case of solids and liquids we have so far been familiar only with specific heat at constant pressure. Determining experimentally the specific heat at the constant volume of a liquid or solid would be a difficult task. Fortunately, it is possible, assuming the validity of the two laws of thermodynamics, to calculate this important quantity from the existing data. The internal energy at constant temperature is almost independent of the volume, in the case of a gas, but can vary consid-erably with the volume in the case of a liquid or solid. Except in rare cases, it increases with increasing volume. The difference between specific heats at constant pressure and constant volume is mainly due to this change in internal energy with vol-ume, as I showed in a previous article where the following purely thermodynamic equation was obtained. (Lewis, 1907, p. 1165)
The mathematical details and the comparisons with the results of the table, according to the work of Lewis, would require another space for discussion. On the other hand, he suggested that Dulong and Petit's law should be modified since:
The law of Dulong and Petit may therefore be modified aid stated as follows: Within the limits of experimental error the atomic heat of constant volume, at a 20℃, is the same for all the solid elements whose atomic weights are greater than that of potassium. (Lewis, 1907, p. 1168)
Given the report above, the background of this law is from the historical point of view, for a better understanding of Boltzmann's arguments of the Kinetic Theory of Gases, which is fundamental to understand the transition from Classical Thermodynamics to Quantum Theory, which had in Planck the necessary insight to modification proposals. In this sense, Laing & Laing (Laing and Laing, 2006) point out that this law is very important to be forgotten historically.
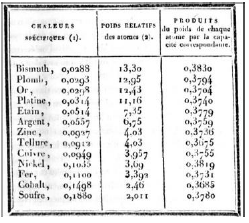
FIGURA 1 Measurements of the specific heats of several simple bodies as a function of the relative weights of the atoms and the product of each atom by the corresponding thermal capacity.
The discussion that Petit and Dulong established after the table (Figure 1) is interesting and long, let us stick to the aspects that maintain a certain relationship with the Boltzmann demonstration in 1866. In this case, we will quote an excerpt from a paragraph, (pp. 403-404).
However, lacking rigorous way of finding out the actual number of atoms of each species that come into a combination, it is conceivable that there must always be something arbitrary in fixing the specific weight of elementary molecules; but the resulting indeterminacy has only two or three numbers, which are the simplest relations between them. (Dulong et al, 1819, pp. 403-404 )
Equation (2), deduced by Boltzmann in his thesis in 1866, justifies the real number of atoms in each component of the substance. Boltzmann starts the demonstration on the topic III - Begründung des Ampèreschen, Dulong-Petitschen und Neumannschen Gesetzes für Gase - (Justification of the Ampère, Dulong-Petit and Neumann law for gases), con-cluding in topic - IV - Beweis des zweiten Hauptsatzes der mechanischen Wärmetheorie - (Proof of the second law of the mechanical theory of heat), applying Clausius' concept of entropy (Boltzmann, 1968), (Boltzmann, 2012).
Before the law was determined, Dulong and Petit used various experimental apparatus to determine the expansion of liquid substances, such as mercury, for example. With these devices they were able to establish the absolute ex-pansion of mercury, publishing some of its results in 1818 (Lewis, 1907).
Between 1816 and 1818, Dulong and Petit published a series of articles, containing numerous comparative measures of the expansion of mercury and air thermometers, in addition to comparing the expansion of some simple elements such as mercury, iron, copper and platinum.
The method used by Petit and Dulong was to heat both the air and mercury thermometers in an oil bath (Heilbron, 1993). The article in which they describe the experiments with relative comparisons has the title: Recherches sur les lois de dilatation des solides, des liquides et des fluides élastiques, et sur la mesure exacte des températures (Research on the laws of expansion of solids, liquids and elastic fluids and the exact measurement of their temperatures).
The process of obtaining this result to draft an empirical law would be theoretically explained decades later, for gases, by Boltzmann in 1866 (Boltzmann, 1968), (Boltzmann, 2012) and for solids by Einstein in 1907 (Dulong, Pierre L., Petit, 1819), using the Planck oscillator quantization hypothesis.
According to Dulong and Petit, the calorimeter measurements performed by Lavoisier and Laplace were very ac-curate and were considered an elegant example of obtaining experimental data. Lavoisier's conjecture that air pro-vides light and heat during the combustion process, taking up in some respects the idea of caloric, demonstrates the readiness for the debate around corpuscular and wave concepts about heat. The apparatus idealized by both shows their skills in merging the theoretical and experimental aspects in the measure of the specific heats for the gases. Lavoisier and Laplace, around 1780, built a calorimeter to perform the measurements, however, they did not obtain the expected results, because not all the melted water entered the meter, and the rest remained in the form of ice, retained by capillarity (Heilbron, 1993).
During this period, two Italian physicists, Macedonian Melloni and Leopoldo Nobili, successfully defended a wave design (Melloni, 1836) for the spread of heat. Their results, published in the article on heat polarization, show the possibility of a wave interpretation similar to the wave design for light, which would lead to the need, later, for a theory based on the presence of the ether, since this entity was used to justify the wave's propagation of light. A more detailed study of the contributions of Melloni and Nobili requires another space (Rosa, 2019).
Physicist and historian of science Stephen G. Brush (Brush, 1970) wrote an important "chapter" about this historical period, relevant to understanding the transition between caloric theory and thermodynamics.
III. BOLTZMANN AND THE SPECIFIC HEAT THEORY FOR GASES WITHOUT STATISTICS AND PROBABILITY
Ludwig Eduard Boltzmann was born in Vienna, Austria on 1844 and died tragically in Duino-Aurisina on 1906, on a vacation trip to rest and recover from his work fatigue. Boltzmann was a genius misunderstood in his day. His story is no less dramatic than that of Van Gogh, who cut his own ear; he was genius and crazy (Johnson, 1918). Boltzmann's health at the time of his death was precarious, he was diagnosed with neurasthenia, in addition to suffering from asthma, chest pains, severe headaches, anxiety and depression (Johnson, 1918).
His death (suicide), as suggested by Mary Jo Nye (Johnson, 1918), may be linked to the dispute between atomists and energists, with Boltzmann being the main defender of the existence of atoms and molecules and energists, with Ernst Mach as his main representative and scientific opponent (Johnson, 1918).
The controversy of atomic debates reached such proportions of crisis at the end of the century that they contributed to the despair and suicide in 1906 of the pro-atomist physicist Ludwig Boltzmann. Most historians and philosophers of science would agree with the role and impact of these debates in the progressive evolution of our knowledge and systematization of the natural world. What was sometimes overlooked in the analysis of the harsh debates is that the crisis in the scientific community of the late 19th century was not only one of evidence and interpretation, but also of scientific methodology and epistemology. The issue was not just atomic theory, but the very aim and structure of physical theory. (Johnson, 1918)
In this article, we will focus on the scientific production of the Austrian physicist and understand why we can con-sider him to be one of the founders of quantum mechanics. His original ideas for interpreting the second law of ther-modynamics from the notions of statistics and probability, had a strong influence on Max Planck.
Based on the hypothesis of quantization of harmonic oscillators in blackbody radiation, Planck used the entropy equa-tion (𝑆=𝑘𝑙𝑜𝑔𝑊+𝑐𝑜𝑛𝑠𝑡.) developed by Boltzmann, profoundly changing the physics of the period. Newton's laws were completely replaced in the interpretation of microphysical phenomena.
Boltzmann completed his doctorate at the age of 22, on February 8, 1867. Under the guidance of Joseph Stefan, he did his work at the University of Viana whose original title is: Über die mechanische Bedeutung des zweiten Hauptsatzes der Wärmetheorie: On the mechanical meaning of the second law of the theory of heat (Boltzmann, 2012).
In the thesis, Boltzmann initially discusses the relationship between the first law of thermodynamics and energy (vis viva), noting that this law was already known. However, the second law, it would be exceptionally peculiar if there was no derivation of it from the principles of Mechanics. Therefore, its objective would be to demonstrate this law analytically, finding a general correspondence with mechanics.
In the first topic, Bestimmung des Begriffes der Temperatur (Definition of the temperature concept), Boltzmann attacks this concept, which is often confused by students of basic education with the idea of warmth. The objective would be to analyze the experimental behavior of the temperature and then define which parameters would control the function. Boltzmann showed the type of function and the physical variables that are significant from an experi-mental point of view for determining the specific heat of gases.
At this point, we call attention to a text by Boltzmann quoted by Olivier Darrigol (1918).
In my opinion, the task of theory is to build a purely internal image of the external world, an image that serves as a guiding star in all of our thinking and experience, somehow completing and extending the thinking process on a large scale through our small-scale representations form. (Darrigol, 1918, p. v, apud Boltzmann, 1890)
In this respect, we agree with Darrigol about Boltzmann's thinking. It is impossible to understand it without pene-trating its mental universe, without understanding its philosophy and the freedom of theoretical construction, the result of a purely mathematical imagination. It is possible to bring both Boltzmann and Poincaré closer together and affirm that their scientific spirits were instrumental in the demolition of the old building whose foundation was New-ton's mechanics in explaining natural phenomena until the end of the 19th century. The construction of a new theo-retical model would prove to be one of the greatest revolutions undertaken by the human mind. It is not just a matter of translating them; it is necessary to know how to interpret them.
Boltzmann was professor of H. Hahn, who obtained a degree in mathematics after defending his qualification with the title: “Observations on the calculation of variations”. Hahn also studied with Hilbert, Klein and Minkowski and together with physicist Ph Frank and economist O. Neurath started a movement for the philosophical interpretation of science (Schmitz, 2019). The discussions arising from the meetings between them were extremely important, as it brought together brilliant young people who, according to François Schimitz, sought a conception of science that could counteract that anti-scientific spirit and Bergson's supposed irrationalism. In this sense, they sought to understand Poincaré's thinking by studying the book: La Science et l’hypothèse, Duhem's physical theory and especially Ernst Mach, the main opponent of Boltzmann's atomism (Nye, 1976), (Lindley, 2001), (Schmitz, 2019).
We return to the implications of the thesis defended by Boltzmann in 1866 on the theory of specific heat of gases, which is fundamental to understand the origins of quantum mechanics from the foundations of thermodynamics.
Boltzmann proposes to define the concept of temperature more precisely and largely, following the mechanics of heat [thermodynamics], since according to him there was still no unanimity among physicists about this concept, with inaccuracy and doubt.
Boltzmann's initial idea when examining the energy exchanges between atoms and molecules is at least curious, since, according to him, it would be necessary to determine initially how an element [molecule] interacts with another without an exchange of energy [vis viva] among them, allowing to know in what conditions the thermal balance could be established. It is at least curious, because, from a mechanical point of view, we always imagine that when two bodies interact with each other, there is necessarily an exchange of energy, a linear and angular moment between them.
Boltzmann notes that thermal equilibrium would happen if the dimensions of the atoms did not interfere with mechanical shocks, as it would change the temperature with each new collision, since the pressure should be the same in any direction (Boltzmann, 2012).
Darrigol considers that the great difficulty of the kinetic theory of gases proposed by Boltzmann was that it was restricted to statistics between molecules, while Gibbs and Maxwell introduced a more powerful tool, the statistical ensembles (Gibbs, 1902;1928; 2012).
For example, it is claimed that Boltzmann's statistical reasoning was confined to molecular statistics, while Gibbs (and Max-well) introduced the most powerful concept of a statistical ensemble. Although many Boltzmann scholars are well aware of this, they still tend to overemphasize Boltzmann's molecular statistics; they often miss their true goals; and still wonder what reasons Boltzmann would have for not questioning them, while he was building his theory. (Darrigol, 1918, p. vi)
Gibbs and Maxwell introduced these statistical sets at a time when Clausius' discussions to understand Carnot's theory of heat (mainly the second law) more clearly and the changes due to Joule's new experimental evidence. The path to the introduction of Entropy as a state variable of the thermodynamic system was originally proposed by Clau-sius in 1862 through a work published in the journal Philosophical Magazine (Clausius, 1862).
Gibbs, based on Clausius' postulates, that the energy of the universe is constant, and that entropy tends to a max-imum, wrote an equation in which entropy is one of the essential concepts to understand the behavior of a system in thermodynamic equilibrium (Klein, 2014).
Gibbs considered this equation fundamental, since it expresses the internal energy of the system in terms of en-tropy and volume, eliminating problems with treatments in terms of heat and work. It would be possible to describe the equations of state expressing temperature and pressure as a function of volume and entropy (Benjamin, 2007).
Clausius proposes a discussion on the idea of disaggregation "disgregation", such as the separation of molecules from each other against internal and external forces. This work was published in the journal Philosophical Magazine in the year of 1862, in two parts, with the titles: “On a modified Form of the second Fundamental Theorem in the Mechanical Theory of Heat” e “On the Application of the Theorem of the Equivalence of Transformations to the Inter-nal Work of a mass of Matter”. The discussion and mathematical demonstration of the concept of disaggregation starts from paragraph 2 of the first publication of the work and Clausius argues that even starting from the definition ∫𝑑𝑄/𝑇≧0 and demonstrating mathematically, the concept will remain abstract. Clausius admits an essential differ-ence between internal and external work, being possible to apply a combination between both. Clausius notes that his first investigations into the mechanical theory of heat led him to assume a general law respecting the dependence between energy in the form of heat and temperature. On the page 86 (Clausius, 1862), (Klein, 2014), the word disgre-gation appears which we quote below an excerpt from the article:
Now the effect of heat always tends to loosen the connexion between the molecules, and so to increase their mean distances from one another. In order to be able to represent this mathematically, we will express the degree in which the molecules of a body are dispersed, by introducing a new magnitude, which we will call the disgregation of the body, and by help of which we can define the effect of heat as simply tending to increase the disgregation. (Clausius, 1862, p. 86)
The discussion is long and could be the subject of another article. We will only use some conclusions published by other authors on the aspect of disaggregation introduced by Clausius to generalize the second law of thermodynamics. For example, Darrigol (Darrigol, 1918), p. 130 claims that Boltzmann proved the existence of the breakdown proposed by Clausius. On the other hand, Pellegrino, Ghibaudi e Cerruti (Pellegrino, Ghibaudi and Cerruti, 2015) conclude that:
The epistemic relevance of disgregation has been pointed out by outstanding scientists, such as Gibbs and Horstmann. We add further elements by showing that Clausius relied on this concept to formalize the Second Law for non-cyclic systems. Further, in agreement withLeff (LEFF, 1996), we show that disgregation, intended as a measure of particles’ dispersion, helps to clarify the meaning of entropy in Clausius’ thought. In this perspective, pre-modern quantities shed light on the comprehension of the Second Law. (Pellegrino, Ghibaudi and Cerruti, 2015, p. 4514)
In the 1865 article, Clausius defines and proposes the term entropy for the amount of heat contained in the body as a function of temperature and disaggregation, the ratio between the sum of the variation of the internal potential energy, the work and the temperature T. That is the same Gibbs equation, with a reinterpretation of the amount of heat contained in the body in terms of internal energy, where the potential molecular energy must be incorporated.
Pellegrino, Ghibaudi and Cerruti (2015), quote an observation by Leff (1996), in which he suggests that Clausius removed from the second edition of his book on the mechanical theory of heat the concept of disaggregation because he thought his result would be incorrect in relation to the application for specific heat:
A further reason, suggested by Leff, is that “Clausius’ disgregation-based theory led him to an incorrect result on specific heats; so Clausius decided to delete disgregation from the second edition of his book on the mechanical theory of heat”. (Pellegrino, Ghibaudi y Cerruti, 2015, p. 4514)
To make this claim, Leff cites the work of Martin J. Klein (2014) - Gibbs on Clausius in which Gibbs receives a letter in June 1889 to reexamine Rudolf Clausius' scientific career, killed in August of that year. In fact, when examining Klein's article, we see, on page 140, that there is an assertion that Clausius carefully omitted such a term.
Thus, when Clausius reworked his papers in to a systematic exposition of thermodynamics for the second edition of his book in 1876, he carefully omitted any mention of disgregation, although he promised to treat it in a third volume, which he did not live to complete. (Klein, 2014, p. 140)
Boltzmann quoted Gibbs in 1883 (Boltzmann, 2012) and he considered that the work of the Austrian physicist was valuable, as he considered aspects of the concept of probability to explain the thermodynamic behavior of molecules. However, Gibbs when introducing his ensembles (Gibbs, 1902) he considered that his representation was more gen-eral to statistical mechanics than those of Maxwell and Boltzmann.
According to Laranjeiras (2002), Boltzmann, by introducing the notions of probability to interpret the 2nd law of thermodynamics in his research program, not only inaugurated the foundations of statistical mechanics, but was able to pave the way for quantum mechanics.
A remarkable presence in this debate, Ludwig Boltzmann (1844-1906), a great defender of the twin flags of mechanism and atomism, developed a rich research program, specifically in kinetic-molecular theory of gases, whose evolution was possible, in addition to a brilliant defense of the mechanistic program, albeit modified, the introduction of probability theory into a fundamental law of physics, the 2nd law of thermodynamics, creating the foundations of modern statistics and even paving the way for quantum theory. (Laranjeiras, 2002, p. 1)
This debate is long, and the conclusions are innumerable, it is not possible in this space to discuss it in detail, just conclude together with other historians of science that it was useful for the new foundations of physics that would be built, transcending Newton's Mechanics.
Boltzmann used Hamilton's principle of minimal mechanical action (Laranjeiras, 2002) to explain the microscopic behavior of temperature and thereby establish a mathematical and physical significance of entropy, which had been established by Clausius in 1865. Louis de Broglie, between 1922 and 1924 also used this principle, however, he set out for a synthesis of quantum mechanics merging the principles of the minimal action of Maupertuis of mechanics and optics of Fermat (Rosa y Martins, 2004; Martins, R. A. y Rosa, 2014), showing the importance of the special theory of relativity formulated by Poincaré, Lorentz and Einstein.
Boltzmann's goal, based on this premise, was to provide a reasonable theoretical justification that would explain the empirical law of Dulong-Petit. Laranjeiras7 believes that the solution presented by Boltzmann based on the con-cept of molecular disaggregation is the first theoretical justification for this law, since, starting from his definition of temperature, expressed by the average of energy kinetics of a single atom, it was possible to find an equation (3) to determine the heat capacity γ (specific heat) of material bodies.
From the infinitesimal variation in temperature, Boltzmann obtained the expression of the variational energy (amount of heat) used by the particles (molecules) that contribute to the temperature variation of the whole body.
This justifies Boltzmann's definition that the amount of heat supplied to the body is the sum of the kinetic energies supplied to each atom. Entropy, in the sense of Clausius, gains a new interpretation, since Boltzmann formalizes the relationships between the amount of heat supplied to bodies and the variation in the movement of each atom in space (Laranjeiras, 2002).
Boltzmann devised a consistent mathematical model that would allow him to discuss the processes of "disaggre-gation" (Z) according to Clausius and would make it possible to justify the atomic-molecular structure of matter, being able to provide, for the first time, a theoretical proof of the empirical law of Dulong-Petit (Laranjeiras, 2002).
The demonstration of the law begins on the topic III - Begründung des Ampèreschen, Dulong-Petitischen und Neu-mannschen Gesetzes für Gase (Boltzmann, 2012) - Fundamentals of the Ampère, Dulong-Petit and Neumann laws for gases. Boltzmann defines the energy (vis viva) of molecules by the relationship 𝑚𝑐2/2 and eliminates for the first time the presence of the ether from the intermolecular medium of gases but keeps it in the interior space of the atom, which seems to contradict its final conclusions on this topic.
It is necessary, for the first time, to abstract the presence of the ether in the gas, whereas previously the ether filled the space inside the atom. The product of the pressure for the volume of the gas would then be given by 𝑝𝑣=2𝑁𝑃/3= 𝑁𝑚𝑐2/3, according to a formula derived from Krönig, Rankine and Clausius. (Boltzmann, 2012, p. 21)
This position adopted by Boltzmann can be considered complex. Why does it keep the intermolecular space unoc-cupied by the ether, while inside the atom the ether is present? Perhaps, to facilitate the collision processes and consequently the heat transfer and the infinitesimal variation of the temperature in the thermodynamic equilibrium.
Poincaré, in his 1912 article, will deduce Planck's law in three different ways without making any conjecture about the presence of ether in the processes of mechanical shocks, however, he does not abstain from trying to develop a theory that would lead to the same results in the presence of ether, according to the Doppler-Fizeau theory.
Historically, it would be necessary to consider this momentary “abandonment” of ether by Boltzmann and to see if this had implications for Albert Einstein's theory, influencing him to abandon it also in favor of the special theory of relativity.
On the other hand, Boltzmann was aware that the molecules should not be rigid and that their elastic deformation would imply emission of radiation, just like the collisions between rigid bodies that emit sound. If these collisions were to occur constantly between the gas molecules, at some point they would totally lose kinetic energy to the ether. Boltzmann imposed the condition of thermal equilibrium between the molecules and the ether (Darrigol, 1918), par-tially justifying the excerpt mentioned above. A justification for the elastic molecules in equilibrium with the ether was given by Marcel Brillouin (Rosa, 2019; Brillouin, 1919) and it may have been one of the factors that led Louis de Broglie to conceive of the electron as a pulsating membrane. Marcell Brillouin's attempt to justify the presence of ether in mechanical movements took place around 1893-94, a period in which he published several articles on the subject.
Returning to the Boltzmann demonstration for the specific heat in the gases, we find that the central point is in the use of the principle of minimal mechanical action or Maupertuis principle. This same principle will be used by Louis de Broglie between 1920 and 1924, together with the Fermat principle (minimal optical action) and the theory of special relativity, to find the equation of the electron wavelength as a function of Planck's constant (h) and the linear momentum (𝑝) (Rosa y Martins, 2004; Martins, R. A. y Rosa, 2014).
Boltzmann started from the definition of the molecular motion P in terms of the ratio between the integral of the molecule's kinetic energy and the temporal integral.
Boltzmann considered that if the product
Considering that the system is composed of N molecules, containing atoms a from simple substances, forming the first element and atoms
getting
Equation (6) is a derivation already obtained by Krönig, Rankine and Clausius. It shows that Boltzmann still preserves the essential parts of the “old” thermodynamics. Equation (7) represents the amount of heat [lebendige Kraft - força viva] that would be equivalent to the work that is added to the system by providing a variation of external heat.
In the sequence, Boltzmann works algebraically on the relations and makes conjectures about the addition of heat in the system until reaching the formula for calculating the number of atoms present in the molecule at constant volume and temperature. Boltzmann knew Loschmidt's result of 1865 which was the first estimate of the measure-ment of the size of the air molecule.
The heat capacity (specific heat) of the molecule was in accordance with the relationship below.
γ is therefore constant as long as we assume that the volume units were obtained at the same temperature and pressure, proportional to the number of atoms in the molecule, therefore, according to the previous law, proportional to the sum of the volumes for simple gases, which form the volume of the substance. Masson considered this law in his treaty “sur corre-lation des propriétés physiques des corps” - (“on the correlation of physical properties of bodies”) confirmed experimentally, but with a few exceptions. It also follows that the specific heat at constant volume, in relation to weight, is proportional to the number of atoms in the molecule divided by the equivalent [gram] of the body. (Boltzmann, 2012, p. 33)
Boltzmann quotes the work M. A. Masson on the correlation between the physical properties of bodies, certainly, paragraph II of topic II - Détermination du rapport des chaleurs spécifiques des gaz (Determination of the relationship between the specific heat of gases) and the paragraph III - Notions sur la théorie méchanique de la chaleur (Under-standing the mechanical theory of heat).
IV. MASSON AND DULONG'S LAW FOR SPECIFIC HEATS - THE SPEED OF SOUND IN GASES
In paragraph II, Masson used Laplace's arguments (Traités de Physique) and other scientists (Nicolás Clément and Charles Desormes, Gay-Lussac and Welter), to determine the speed of sound propagation in the gases. Nicolás Clément and Charles Desormes they did an experiment in 1819 whose objective would be the determination of the molar calorific capacities (γ) at constant pressure.
This experiment was later perfected by Welter and Gay-Lussac. The difference between the two is in the way the gas is released; Gay-Lussac and Welter proposed a quick opening of the valve that controls the container, but, accord-ing to Moore, some changes should be made to be able to obtain an adiabatic transformation, with a drop in temper-ature (Moore, 1984).
Masson described that by using the Gay-Lussac and Welter method, he let the gas dilate subitement (suddenly), making it possible to calculate the value of the constant K.
The variables
This K would be used in paragraph III of the same topic to confirm the validity of Dulong's law.
This K would be used in paragraph III of the same topic to confirm the validity of Dulong's law.
The specific heat of gases at constant pressure or constant volume is given by the knowledge of the K coefficient, if we accept the Dulong hypothesis: The specific heat of gases at constant volume per unit of volume, are in the inverse ratio of the temperature rises produced in these gases by the same compression. (Masson, 1858, p. 270)
In paragraph III - Notions sur la théorie méchanique de la chaleur - Understanding the mechanical theory of heat, Masson admits to adopting the same principle that physicists and geometers had previously adopted, that is, in cases where the mechanical work is produced by heat, there will be a heat expenditure proportional to the work performed. Conversely, this amount of heat can be regenerated through the same mechanical work as the previous one. This means that Masson is considering the principle of reversibility through the principle of minimal mechanical action.
According to the position adopted by Masson, who considers this principle to be very important and fruitful, ex-perience shows that Dulong's law results in the correct value of the mechanical equivalent of heat.
This important and fruitful principle, which is sanctioned by experience and facts, allows us to simply establish Dulong's law and give the true value of the mechanical equivalent to heat. (Masson, 1858, p. 270)
Masson considers a cylinder of 1.0 m2 in diameter, containing 1.0 kg of air under a piston of negligible weight, supporting the atmospheric pressure P. The work will be given by the relationship below from the density definitions
In this way, Masson wrote the relationship for the job by the expression below:
Then, Masson developed the mathematical calculations, showing Dulong's law as a function of the constant K, concluding that:
The principle that provided us with a simple and accurate demonstration of Dulong's law, and that gave us the true value of A, will lead us to some new and notable consequences that will be needed in later work, to the correlation of the physical properties of bodies. (Masson, 1858, p. 272)
Masson was right in saying that new consequences would come from this law, because it was exactly the attempt to explain it that provided new thermodynamics and consequently the change from classical mechanics to quantum mechanics. The theoretical solution for the material bodies specific heat was resolved “in a definitive way” by a work published by Peter Debye in 1912 (Debye, 1912), the same year that Poincaré published his seminal article on Planck's hypothesis of blackbody radiation, perhaps under the influence of Poincaré's participation in the first Solvay Council in October 1911.
The final equation, deduced by Masson, according to him, differs from the Dulong equation by a square root factor
Quoting Dulong's work on calculating the speed of sound in a gas, Masson concludes that it would be unnecessary to consider Dulong's previous memories, since work on determining the speed of sound in gases would be sufficient to explain the experimental results according to the theory, despite the inaccuracies of the measurements.
Despite the inaccuracy of the procedures used by Dulong to recognize the true position of the knots in the sound tubes, it must, however, be recognized that a mobile piston always indicates the same nodal lines in the same tube and for any gas, the elastic fluids vibrate according to the same laws, whatever their nature. (Masson, 1858, p. 277)
This law to which Masson refers, are the theorems of Laplace, Poisson and Carnot of the theory of heat. Masson developed his theory from the idea that the heat acting on the bodies produces two effects: a molecular one that depends on the nature of the bodies, which would be the internal work and, the other external work, whose objective would be to overcome the external influences (external forces). Masson cited page 481, Tomo XCIII of a work by Claussius published in Poggendorff’s Annalen.
V. BOLTZMANN AND THE SPECIFIC HEAT THEORY FOR GASES
After this brief account of the consequences of Masson's experiments and Dulong's research, we emphasize that Boltzmann was in possession of some important theoretical and experimental results to develop his own theory on the determination of specific heats in gases.
Boltzmann found an expression that made it possible to determine the number of atoms in the molecule. Probably he was already aware of the article by Loschmidt (Loschmidt, 1865) that allows determining the size of the molecule of the substance, although he did not quote it in his thesis. The relationship below was obtained analogously as Masson, who determined Dulong's law for vibrations in gases:
where:
γ is, therefore, constant, since we assume that the volume measurements were obtained at the same temperature and pressure, proportional to the number of atoms in the molecule, therefore, according to the previous law, proportional to the sum of the volumes of the simple gases that form the volume of the substance. (Boltzmann, 2012, p. 22)
The final part of the topic III Boltzmann's thesis presents relevant discussions from the point of view of the foun-dations of molecular mechanics based on the kinetic theory of gases. Boltzmann makes considerations about the im-portance of the presence of ether in the molecular construction process from the absorption of heat by the substance. The negligence of this substance, according to Boltzmann, would not be decisive to alter the experimental results and consequently the theoretical construction of the law of specific heats of gases. Adjusting Ampère's law and observing that Masson's law, determined from the propagation of sound in a closed tube, containing a certain gas is an excep-tion, that is, even with the experimental results updated in relation to the previous ones, Boltzmann admits being premature the establishment of an atomic-molecular theory for gases; the Clausius entropy hypothesis remaining, as an alternative to the previous ideas of Dulong-Petit and Masson.
Below we place an important excerpt in which Boltzmann refers directly to the ether itself in a direct way and not the need to take into account its presence in the intermolecular medium, which neither would affect the process of heat absorption by the substance in any way, nor the formation of the molecule.
This formula would allow an immediate calculation of the number of atoms in the molecule; here, however, a peculiar diffi-culty arises in which the calculation, assuming 𝛾′/𝛾 for air and most simple gases = 1.411, provides a number n slightly greater than 1 and 1/2, a result that is generally it is not correct, but it is conceivable that we have to assume that the gases in question consist of two parts, one of which contains 1 atom in the molecule and the other part, 2 atoms in the molecule. This disagreement is not very likely to result from the neglect of the etheric mass present in gases [...] If we disregard the absolute value of these numbers, we find that they do not behave like the atomic numbers of the molecule, calculated according to Ampère's law, but as normally 1 or 2 larger integers, although it seems strange that they do it this way. Mas-son's values for (𝛾′− 𝛾)/𝛾 determined from the sound propagation in a tube containing gas, is an exceptional behavior, as is the number of atoms. If we add that the numbers found by Dulong behave very differently, not to mention previous attempts, it must be admitted that the experimental data are not yet in agreement, to provide reliable theoretical conclu-sions about the composition of the gases. However, the Clausius hypothesis seems to be the most likely, for simple gases, at least 2 atoms, when combined to form a molecule. (Boltzmann, 2012, pp. 22-23)
We draw attention to the fact that Boltzmann was not satisfied with the experimental results in his day, although he accepted it as a good approximation, but, still insufficient for a consistent theoretical construction on the molecular composition of gases. Another relevant aspect is the change of route in his research program, starting to consider that Clausius' hypothesis of entropy could lead to a new theory allowing the interpretation of the laws of thermodynamics through a new mathematical model, the statistical-probabilistic one.
René Dugas, in his book La théorie physique au sens de Boltzmann accurately describes the importance of Boltz-mann's scientific and philosophical thinking for the further development of physics (Dugas, 1959).
Ludwig Boltzmann, whose work belongs to the last third of the 19th century, is one of the thinkers whose influence was very profound in the development of modern science. In this regard, it is sufficient to cite the works of Planck and Einstein on the statistical theory of radiation, the quanta and photon hypothesis, which are originally presented as an illustration of Boltz-mann's principle about interpreting entropy in terms of probabilities. (Dugas, 1959, p. 17)
In fact, we agree with Dugas in this sense because Planck used Boltzmann's interpretation of entropy in terms of the 1872 article in his 1900 publications. In addition, Planck used the idea of quantum, present in a published article by Boltzmann in 1884. In relation to Einstein, the important German physicist, by publishing an article on the deter-mination of specific heat in solids in 1907, using Planck's hypothesis of quantification of the harmonic oscillators of blackbody radiation, was able to theoretically explain the empirical law of Dulong and Petit, calling the attention of the scientific community at the time and, allowing an important debate in the first Solvay Council, in which, Poincaré was present.
VI. CONCLUSIONS
The determination of specific heat, both from an experimental and theoretical point of view, can be considered as a fundamental prerequisite for structural changes in the phenomenology and epistemology of physics in the late 19th century. It served as a precursor to the interpretation and mathematical modeling of microphysical phenomena, set-ting the stage for the introduction of Planck's hypothesis of blackbody radiation in 1900. A new way of interpreting the interactions between radiation and matter was yet to be conceived, replacing the well-known and widely used Newton mechanics.
Dulong and Petit were part of a period in which there was a very intense debate in relation to the physical inter-pretation of heat, whether it could be conceived from a corpuscular point of view, with the ideas of phlogistic and caloric, or whether it would have a purely undulating behavior, like the light. The idea of radiant heat was promising a priori with the publications, both theoretical and experimental, by Macedonio Melloni and Leopoldo Nobili, but over time it lost its strength, being forgotten and replaced by a new concept, that of Clausius, who introduced a new con-cept in physics, Entropy (Rosa, 2019; Aurani, 1992).
In this sense, it is undeniable that the main theoretical physicist to give a deeper physical and mathematical mean-ing to this constant was Ludwig Boltzmann. We analyzed from the origin of the Dulong-Petit law, commenting on the controversy of its authorship, until the defense of Boltzmann's doctoral thesis, because we consider that the analytical demonstration proposed by the Austrian theoretical physicist is a preparation for the reinterpretation of the thermo-dynamic laws a from the new ideas introduced by Clausius. In this sense, we are in complete agreement with Olivier Darrigol about the freedom of theoretical creation. It must allow the scientist to use his full creative potential, helping him to submerge himself in the deepest layers of his imagination, bringing to the most rational surface an explanation for the behavior of nature.
Boltzmann's scientific works, as well as his philosophical thinking, were not only fundamental, but essential to open a clearing in the dense obscure layer of the amount of unexplained experimental results. The idea of the nature of heat in the interaction with matter had previously been discussed by other scientists, using the concept of molecular constitution of matter, such as: D. Bernoulli, who in 1738, was already dealing with a model of particles with impacts on the walls of the container to explain the pressure of “elastic fluids”; Lavoisier (1789) discussed the expansion under heating in terms of the separation of particles from the bodies among themselves and Avogadro's proposal for the number of molecules proportional to the volume of the gas had already been conceived in 1845. The defense of the atomic-molecular character of matter, cost Boltzmann dearly, according to historian Mary Jo Nye, cost him his life. Another aspect that we consider relevant in his first ideas is the abandonment of the presence of the ether in relation to the intermolecular space. In a rational and original way, Boltzmann envisioned the law of the least effort present in nature, using the principle of minimal mechanical action or Maupertuis' principle.
Equation (14), which defines how to calculate the number of atoms in the molecule of a simple substance, a gas, as a function of specific heat, is not in contradiction with the experimental results of Dulong and Masson, if this ethe-real material substance is neglected in the processes of interaction between molecules.
Nicht viel wahrscheinlicher ist die Annahme, daβ diese Nichtübereinstimmung von der Vernachlässigung der im Gase vorhandenen Äthermasse herrühre… It is not very likely that this disagreement is due to the negligence of the etheric mass present in the gases. (Boltzmann, 2012, p. 22)
Boltzmann neglected the presence of ether in interactions between molecules but kept it internally in the atom. He did not justify this "presence-absence" of the ether, perhaps because he was quite sure of the Loschmidt calcula-tion of the size of the air molecule, but he started the basis for a profound epistemological change in the foundations of physics. We can call this period, from the observation of Dulong-Petit's law (1819) to the introduction of the en-tropic atomic-molecular structure (1866), the transition period from the “old” to the “new” physics.














