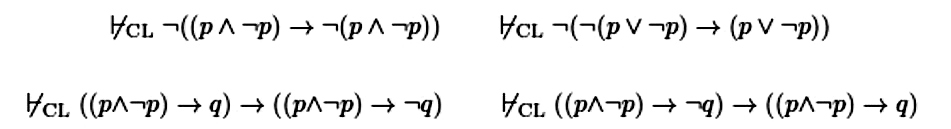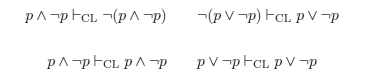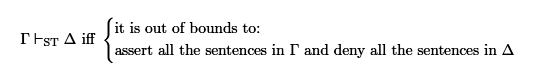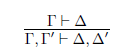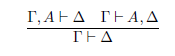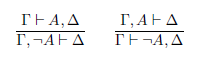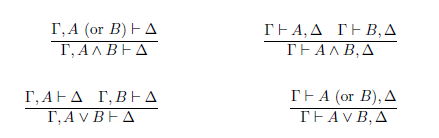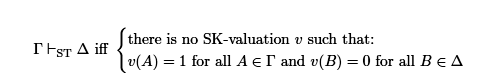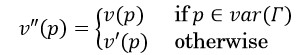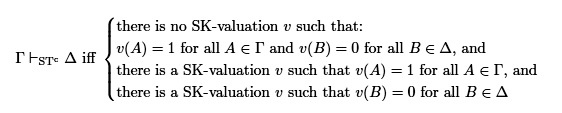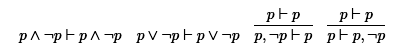Connexive logics can be roughly described as non-classical systems having in high esteem the idea that there is a certain relation in which some formulas should not stand. To be more specific—while keeping talk of this relation intentionally unspecified—the connexive ideas can be summarized as follows. Firstly, there is a certain relation in which a formula A and its negation ¬A should not stand. Secondly, if the pair of formulas A and B stand in this very same relation, then the pair of formulas A and ¬B should not stand in this relation. Variations of these requirements are usually also regarded as deeply entrenched with connexivity. ¹

The aim of this paper is to provide an inferentialist motivation for a logic belonging in the connexive family, by borrowing the bilateralist interpretation for Classical Logic without the Cut rule—i.e. for the strict-tolerant logic ST—defended by David Ripley in e.g. Ripley (²⁰¹³) and thoroughly examined in Ripley (²⁰¹⁸). ² With the present attempt we hope to broaden the available interpretations for connexive logics, showing they can be rightfully motivated in terms of certain constraints imposed on the speech acts of assertion and denial. ³

To this extent, in §1 we present connexive logics and review their relation with Classical Logic. After that, an extensive discussion of the logic ST and its bilateralist interpretation is provided in §2, along with some technical remarks concerning it. This is, later, followed by a number of considerations on the relevance of the speech acts involved in rendering an argument as valid, which lead us to consider and analyze a connexive fragment of ST in §3. We conclude by offering some closing remarks in §4.

1. Connexive Logics

As we said above, connexive logics embody the idea that a certain relation should not hold between some formulas. Among the systems discussed in the literature, a remarkable portion concerns frameworks which formalize the connexive ideas by means of different criteria pertaining to an implication connective. In other words, most contemporary works in connexive logics think of the aforementioned relation between formulas in terms of their connection through a conditional.

Along this line, systems were asked to include among their theorems every substitution instance of certain formulas—honorarily referred to as thesis—which allegedly internalize some connexive ideas due to Aristotle and Boethius, whence the labels below. Thus, a system is taken to be implicationally connexive if it is such that:

AT→ 1

For every formula A, ⊢¬(A→¬A)

AT→ 2

For every formula A, ⊢¬(¬A→A)

BT→ 1

For all formulas A and B, ⊢(A→B)→¬(A→¬B)

BT→ 2

For all formulas A and B, ⊢(A→¬B)→¬(A→B)

Now, it has been noticed as early as in McCall (¹⁹⁶⁶) that the characteristic connexive theses are not a part of Classical propositional Logic (hereafter, CL), which justifies labelling connexive logics as supraclassical. Interestingly, this is not the only thing that can be said about the frustrating relation of CL with the connexive principles. It has been sharply diagnosed, e.g. in Ferguson (²⁰¹⁵), that it is contradictory and tautological formulas that tend to stick their noses in the counterexamples of all of these theses, as is shown in the examples below.

As an alternative to implicational connexive systems, other scholars discussed the incarnation of the connexive ideas as formalized by criteria concerning an entailment relation. Among them Graham Priest (^1999a), Thomas Ferguson (²⁰¹⁵), Luis Estrada-González and Elisángela Ramirez-Cámara (²⁰¹⁶), Heinrich Wansing and Daniel Skurt (²⁰¹⁸). In fact, some, but not much, of the published material in contemporary connexive literature is concerned with understanding the aforementioned relation between formulas in terms of their connection through logical consequence. This is the kind of connexivity that we will be exploring in relation to ST. This is, furthermore, the kind of connexivity that we will show to be capable of an inferentialist and, in fact, a bilateralist interpretation. ⁴

In this vein, systems are asked to invalidate every substitution instance of certain schematic inferences—related to the thesis mentioned above—thereby allegedly internalizing the original connexive ideas, now in an inferential form. Thus, a system can be taken to be inferentially connexive if it is such that:

AT⊢ 1

For no formula A, A⊢ ¬A

AT⊢ 2

For no formula A, ¬A ⊢A

BT⊢ 1

For all formulas A and B, if A ⊢ B, then not (A ⊢ ¬ B)

BT⊢ 2

For all formulas A and B, if A⊢¬B, then not (A ⊢ B)

Interestingly, these conditions can be seen as proper incarnations of the following conditions suggested by Andreas Kapsner (²⁰¹²).

Int1 Surely it is not the case that a proposition A should imply its own negation (or the other way around).

Int2 Surely if A implies B, then A does not imply not-B (and if A implies not-B, then A does not imply B).

with the slight difference that, whereas Kapsner’s conditions focus on implication, the previously mentioned inferential conditions focus on entailment. Thus, they shall perhaps be seen as formalizing the corresponding modifications, detailed below. ⁵

Int1* Surely it is not the case that a proposition A should entail its own negation (or the other way around).

Int2* Surely if A entails B, then A does not entail not-B (and if A entails not-B, then A does not entail B).

Once again, as noted in Wansing, Omori, and Ferguson (2016), contradictory and tautological formulas are saliently featured in the counterexamples to these connexive requirements. As it is easily seen, classical counterexamples can be designed by conveniently focusing on contradictory formulas as premises in some cases, and on tautological formulas as conclusions in some others. The inferences below, for instance, witness this phenomenon.

In light of this, it appears to be quite in place to say that inferential connexivity is bound to suppress the explosive power of contradictory premises, and the dilutive power of tautological conclusions. Premises and conclusions of these types, however, exhibit these powers in the context of ST for reasons completely coherent with its inferentialist interpretation. In what follows, then, we will devote ourselves to presenting this interpretation, and showing how it can be put to work in order to account for a connexive fragment of ST.

2. Bilateralism and Classical Logic

A clear, short and powerful introduction to inferentialism and to the particular version of it represented by bilateralism, is provided by Ripley (²⁰¹⁸) in e.g. §1.1 and can be exemplified with the next quote appearing in §2.1.

Inferentialism is the view that meanings are to be explained in terms of which inferences are valid. Bilateralism, a particular form of inferentialism defended in Restall (²⁰⁰⁵) and Rumfitt (²⁰⁰⁰), is the view that which inferences are valid is itself to be explained in terms of conditions on assertion and denial.

Ripley’s own bilateralist account can be succinctly explained saying that, for him, inferences of the form Γ ⊢ Δ are taken to represent positions, i.e. pairs of collections of speech acts, particularly of the assertion of all the sentences in Γ and the denial of all the sentences in Δ. Thus, while some positions are in bounds, others are out of bounds. The fulcrum of this account is the brilliant idea of taking arguments Γ⊢Δ to stand in for the claim that the position built from the assertion of all the sentences in Γ and the denial of all the sentences in Δ is out of bounds. As Ripley also puts it sometimes, this means that there is a clash between the assertions and the denials contained in the said position.

Starting from this reading of sequents as positions, it is argued that this allows for a bilateralist interpretation of Classical Logic—to all the essential sequent rules of Classical Logic, that is, as they are presented in e.g. Gentzen (^1935a, ^1935b). Or something really close to that, as discussed e.g. in Ripley (²⁰¹⁸, §1.3). As we will see below, this will account for Classical Logic without the Cut rule. This is the system which, by now, it is folklore to call ST. In symbols:

To see how this allows to account for Classical Logic without the Cut rule, let us first review the arguments giving a bilateralist interpretation of the usual structural rules, focusing later on negation—leaving the case of the remaining connectives for another occasion. Concerning the structural rules, then, let us notice that since the framework is intended to work with sets of assertions and denials, the rules of Contraction and Exchange are somehow built-in the setting itself and, hence, there is no need to make a case for them.

The structural rule of Reflexivity or Identity, that is:

A ⊢ A

is easily justifiable by noting that—in the context of the current interpretation—rejecting it would amount to saying that for some sentence A, the position asserting A and denying A is in bounds. But such a pair of speech acts is, perhaps, the paradigmatic case of an out of bounds position (Ripley, ²⁰¹³, §2.1 and Ripley, ²⁰¹⁸, §2.3.1). Thus, Reflexivity must be admitted.

This is not to say, as Ripley himself admits, that there could not be other inferentialist—or even bilateralist—approaches rejecting Reflexivity on reasonable grounds, as French does in French (²⁰¹⁶). However, French’s proposal in particular, does not motivate the rejection of Reflexivity in the plausibility of an overlap between the assertion and simultaneous denial of A. ⁶ Whence, it does not constitute a rival theory to Ripley’s, but instead an alternative to it focused on modeling a different inferential phenomenon. ⁷

The case of the Weakening rules, summarized in Ripley’s Dilution rule, namely:

is also briefly discussed. In fact, all that Ripley says is that “if a position is out of bounds already, then adding more assertions and denials cannot bring it back into bounds” (Ripley, ²⁰¹³, §2.1 and Ripley, ²⁰¹⁸, §2.3.2). Adding elsewhere that what would bring it in bounds would be a number of retractions, i.e. of actions of taking back some of the assertions and denials contained in the out of bounds position. ⁸ Thus, Weakening must be admitted.

Again, this should not be interpreted as saying that there might be no approach, similar to Ripley’s, which might reject Weakening on reasonable grounds. In fact, Ripley himself and his collaborators discussed alternatives of this sort in Cobreros et al. (²⁰¹⁷). However, such proposals do not motivate the rejection of Weakening in the plausibility of the addition of further assertions and denials taking an out of bounds positions, back into the bounds. Whence, it does not constitute a direct attack on the previous arguments, but rather an attempt focused on modeling different phenomena. ⁹

The most interesting case to be discussed, though, is that of Cut:

Ripley takes Cut to incarnate an extensibility constraint on in bounds positions, by means of which, as referred in e.g. Ripley (²⁰¹⁸, §2.3.4) and as can be seen in the following quote from Ripley (²⁰¹³, §2.2)

if, given assertion of Γ and denial of Δ, it is out of bounds to assert A and out of bounds to deny A, then asserting Γ and denying Δ is already out of bounds. Any position that is in bounds must be extensible, either to a in-bounds position that asserts A or to one that denies A.

Furthermore, Ripley adds, such an extensibility constraint might happen to the positions of our language, but it is certainly unfair to require it in advance. There are some positions which are, so to speak, in a middle ground concerning some formulas A: they neither assert it, nor reject it. Thus, the structural rule of Cut must not be admitted, this being the hallmark of the ST account. ¹⁰

Having reviewed the bilateralist case for embracing and discarding the structural rules, let us now briefly state how this account also allows us to motivate an interesting take on negation, as it is featured in Classical Logic. A connective, that is, whose characteristic rules are:

These rules allegedly portray negation as representing the speech act of denial. In this vein, the main contribution of bilateralism lies in proposing to understand negation as getting its meaning through denial, contrary to the usual understanding of denial as the assertion of a negation (Ripley, ²⁰¹³, §2.1). In fact, the rules appearing above are argued for by noting that asserting ¬A is equivalent to denying A, while denying ¬A is equivalent to asserting A.

Concerning the usual sequent rules for conjunction and disjunction, belonging to the standard presentations of Classical Logic, namely:

Similar philosophical reasons of this bilateralist sort can be provided to justify their adoption. We omit them here for the sake of brevity, but arguments for their reasonableness can be found in many of Ripley’s works, e.g. Ripley (²⁰¹³). The previous considerations characterize Classical Logic without the Cut rule—i.e. the non-transitive logic that many people know, and to which we refer as ST. One of the main attributes of which is, and this may or may not come as a surprise, that its set of valid inferences are exactly those of Classical Logic.

Despite the strong inferentialist inclination of the remarks included above, it shall nevertheless be noted that ST has an equivalent formulation in semantic terms, as discussed e.g. in Ripley (²⁰¹⁸, §4.3.2). This can be done by focusing, instead of on Classical two-valued valuations (CL-valuations, henceforth), on Strong Kleene valuations (SK-valuations, hereafter) ranging over the set {1,1/2,0}, interpreting the connectives as in Kleene (¹⁹⁵²), taking logical consequence to be defined as follows. ¹¹

Following Ripley, though, in the rest of our discussion we will be appealing to the models, although it should be kept in mind that the inferential perspective on these phenomena is just as important as the semantic one.

To close this section let us highlight that, as with CL, the connexively abhorred inferences are not completely banned from ST. This is, precisely, because the previously mentioned contradiction-involving and tautology-involving counterexamples are still present in ST—as all inferences valid in CL are valid in ST. In other words, these counterexamples are explained by the fact that Weakening is valid, and that in ST, for every formula A:

A∧¬A⊢∅ ∅⊢A∨¬A

Interestingly, in terms of ST’s inferentialist interpretation these inferences correspond to the assertion of A∧¬A being out of bounds and, respectively, to the denial of A∨¬A being out of bounds—regardless of the A in question. In turn, these phenomena are explained by the just outlined bilateralist account of negation. On the one hand, asserting A∧¬Arequires asserting both A and ¬A, on the other, denying A∨¬A requires denying both A and ¬A. It is easy to observe how this puts someone holding this position immediately out of bounds, as this will in the end mean that A is both asserted and denied—something ST takes to be the paradigmatic example of an out of bounds position. The moral is, therefore, that the connexive requirements cannot be met in ST, because of the particular conditions set for positions to be out of bounds.

One may wonder whether or not this entire relevantist project clashes with the motivations that might lead someone to endorse ST. Indeed, among such motivations we find that of offering a sufficiently naive theory of transparent truth, by means of which it is expected that some sentences—e.g. paradoxical sentences—end up entailing their own negations. But it is rather obvious that paradoxical sentences entailing their own negations in ST is a feature of the way in which logical consequence is defined, and not a feature of the way in which logical consequence is motivated, i.e. in inferentialist terms. And this is, of course, orthogonal to the issue of transparent truth—i.e. of the truth-predication of a sentence being assertable (deniable) whenever that very sentence is assertable (deniable). ¹²

Thus, advertising the discussion of a connexive logic related to ST might create the expectations that we are going to deal with a different conception of the bounds which could, perhaps, allow for the assertion of A∧¬A to be in bounds and which could also allow for the denial of A∨¬A to be in bounds. Although an interesting option, we will not explore this avenue here. As explained previously, this will boil down to the simultaneous assertion and denial of A being possibly in bounds, and that is something we do not want to commit to. ¹³ Instead of taking this route, in the next section we will motivate a connexive system in the vicinity of ST by looking at positions which are out of bounds—taking the very same conception of the bounds that is dear to ST—but requiring of the said assertions and denials to make a relevant contribution to render the position in question out of bounds. As such, the exploration of connexivity in relation to ST will be mainly stemming out of an investigation of relevance and its link to ST. By means of establishing an independently motivated relevant logic, built following the inferentialist intuitions behind ST, connexivity will appear as an epiphenomenon which is worth noticing.

3. Relevant Assertion and Denial

Even though, as explained in the previous section, ST focuses on a notion of inference designed to portray the clash of certain simultaneous speech acts of assertion and denial, sometimes the assertions and denials contained in the said positions do not make an essential contribution to the substantiation of this clash. This is, for example, the case of the assertion or denial of any formula B, featured in the positions corresponding to the schematic arguments below.

A∧¬A⊢B B⊢A∨¬A

One may wonder, therefore, if there is any fragment of ST working with a different conception of what it is for an argument to be valid. A conception, that is, which takes as a necessary condition the simultaneous concurrence of the assertion of the premises Γ and the denial of the conclusions Δ contained in the corresponding position, for this position to be out of bounds—and, hence, for Γ⊢Δ to be valid. Our aim in this section is not only to show that the answer to this question is affirmative, but also that the particular way in which we will prove it to be so will relate, quite naturally we think, to the satisfaction of the connexive requirements. Let us flag out, in passing, that the discussion in what follows will resemble—although in a different setting, i.e. that of inferentialism—some of the null account of negation discussed by Graham Priest (^1999a), that is, the account according to which contradictions have no semantic content at all.

In a nutshell, we propose to ask of an out of bounds position that the assertion of the premises and the denial of the conclusions contained in it are not out of bounds per se—i.e. when considered as separate collections of speech acts—but only in conjunction. This leads us to consider a fragment of ST that we will call ST^c. We define next what it means for an argument to be valid in this system:

Why would one even care about such a fragment of the logic developed by Ripley et al.? Although it is true that ST classifies an argument Γ⊢Δ as valid whenever the position consisting of the assertion of all the members of Γ and the denial of all the members of Δ clashes, it is worth noticing that—metaphorically speaking—some of these clashes appear to happen within the bounds, while some of them happen outside the bounds.

To wit, the clashes generated by the positions p⊢p∨q and p∧q⊢p represent examples of the first kind, whereas the clashes generated by the positions p∧¬p⊢q and q⊢p∨¬p represent examples of the second kind. For the latter ones, the problem is already there, respectively, in asserting the premises and in denying the conclusions. The additional speech acts included in such positions do not contribute—not even a single bit—to the problematic nature of these. For the former, the problem is, properly speaking, the result of the encounter of the assertions and denials included in the position held. None of such assertions and denials, considered on their own, is essentially problematic. In this vein, we can say that clashes of this kind are genuine clashes while clashes of the remaining type seem to be somewhat derivative.

Our discussion of the system ST^c, then, can be seen as aiming at clashes of this seemingly more genuine kind. That is to say, at clashes between speech acts which are in a trajectory that intrinsically makes them collide with one another—without having, so to say, collided with themselves first. This does not mean that clashes happening outside the bounds are uninteresting, but rather that clashes within the bounds have some relevant features which make them specifically attractive to analyze.

The use of the term relevant is absolutely non innocent here. Thus, although the conditions refining ST consequence might look rather ad hoc at first glance, it is also true that they pinpoint a specific fragment of ST embodying a notion of consequence that is quite faithful to the original idea of material consequence motivating ST. Material consequence is usually taken to have relevant features, asking of the premises to be connected somehow to the conclusion. In the more technical studies about logical consequence, these ideas gave birth to the requirement—discussed e.g. in Anderson and Belnap (¹⁹⁷⁵)—that premises and conclusion should have some topic or subject-matter in common. This was, later, modeled in terms of propositional variable-sharing principles between the sentences appearing in the premises and conclusions. But the more informal conception that the premises must be relevant to establish the conclusion could also be respected, in the fragment of ST that we are discussing here, in a rather novel way.

In fact, if we consider positions which are out of bounds, but whose assertions (denials) alone are sufficient, on their own, to render the given position out of bounds, then any denials (assertions) contained in it would be utterly irrelevant in the generation of the said clash. Contrary to this, given an out of bounds position Γ⊢Δ we say that the assertion of a certain member of Γ is a relevant assertion, if the position resulting from taking back the said assertion is in bounds. Analogously, given an out of bounds position Γ⊢Δ we say that the denial of a certain member of Δ is a relevant denial, if the position resulting from taking it back is in bounds. Indeed, by focusing on ST^c we are after a notion of logical consequence, understood in inferentialist terms, such that both the assertions and the denials contained in a given position are relevant—in this technical sense—to render it out of bounds. Or, which is the same, after a notion of logical consequence for which both the premises and conclusions are relevant in rendering the corresponding argument valid.

It is remarkable to notice that this rather informal approach to the notion of relevance ends up nevertheless inducing a notion which complies with the variable-sharing requirement of Anderson and Belnap (¹⁹⁷⁵). This can be observed by looking at the next helpful reformulation of logical consequence in ST^c, and taking into account some facts stated below, which are in line with observations made in Ferguson (²⁰¹⁵) and Wansing, Omori and Ferguson (²⁰¹⁶).

Thus, let Σ¬={¬A∣A∈Σ} for all sets of formulas Σ. We can account for ST^c as follows:

Fact 1. If Γ is classically satisfiable, ¬Δ is classically satisfiable, and Γ ⊢_CL Δ, then Γ and Δ share some propositional variable.

Proof. Assume Γ is classically satisfiable, ¬Δ is classically satisfiable, and Γ ⊢_CL Δ. Suppose, for the sake of contradiction, that Γ and Δ do not share any propositional variable. Whence, all valuations assign values to the propositional variables of Γ and Δ independently, and therefore to Γ and Δ. By hypothesis, we know that Γ is satisfiable, i.e. that there is a CL-valuation v such that v(A)=1 for all A∈Γ. We also know that ¬Δ is classically satisfiable, i.e. that there is a CL-valuation v’ such that v(¬B)=1 for all B∈Δ, whence v’(B)=0 for all B∈Δ. Let var(Γ) denote the set of propositional variables appearing in Γ. By the above, then, we can construct a valuation v″ such that

Which will make v″ be a CL-valuation such that v″(A)=1 for all A∈Γ, while v’(B)=0 for all B∈Δ. But this makes v″ witness the failure of Γ ⊢CL Δ, which contradicts our initial hypothesis. Therefore, Γ and Δ share some propositional variable.

Corollary 2. If Γ and Δ are such that Γ ⊢_STc Δ, then Γ and Δ share some propositional variable.

Proof. If Γ ⊢ST^c Δ, then by definition Γ is classically satisfiable, ¬Δ is classically satisfiable, and Γ ⊢_ST Δ. But we know that Γ ⊢_ST Δ if and only if Γ ⊢_CL Δ. Whence, by the previously proved fact, we have our desired conclusion.

Having established the relevant nature of the valid inferences of our system ST^c, we shall now comment on yet another important feature of its notion of logical consequence. Namely, its relation with inferential connexivity.

Thus, given our previous considerations concerning ST falling short of satisfying the connexive requirements, it should be evident that its fragment ST^c fares better in this regard. In fact, it is as easy to verify that ST^c complies with all of these criteria, as it is to observe that the explosive power of contradictions as well as the dilutive power of tautologies are suppressed from its notion of logical consequence, due to the additional relevantist constraints.

Fact 3. For no formula A, A ⊢_STc ¬A. Similarly, for no formula A, ¬A ⊢_STc A.

Proof. Suppose A ⊢_STc ¬A. By definition, this implies that A ⊢_ST ¬A, and that A is classically satisfiable. The former implies that there is no SK-valuation v such that v(A)=1 and v(¬A)=0, whereas the latter implies that there is a CL-valuation v’, which is a SK-valuation too, such that v’(A)=1. But, then, v’ is such that v’(¬A)=0, whence we arrive at a contradiction which shows that our initial assumption is untenable. Thus, it is not the case that A ⊢_STc ¬A. The proof of the remaining direction is similar.

Fact 4. For no formulas A and B, both A ⊢_STc B and A ⊢_STc ¬B. Similarly, for no formulas A and B, both A ⊢_STc B and ¬A ⊢_STc B.

Proof. Suppose A ⊢_STc B and A ⊢_STc ¬B. By definition, this implies that A ⊢_ST B and A ⊢_ST ¬B, and that A, B and ¬B are classically satisfiable. The former implies that there is no SK-valuation v such that v(A)=1 and v(B)=0, and that there is no SK-valuation v such that v(A)=1 and v(¬B)=0. From this, we may infer that there is no SK-valuation v such that v(A)=1 and v(B∧¬B)=0. But this can only happen if there is no SK-valuation v such that v(A)=1, which implies that A is not classically satisfiable after all, rendering our initial assumption untenable. Thus, for no formulas A and B, both A ⊢_ST B and A ⊢_STc ¬B. The proof of the remaining fact is similar.

An informed reader might have observed that our connexivity-inducing provisos put on top of ST consequence resemble quite closely those employed by Graham Priest (¹⁹⁹⁹a) when defining his so-called symmetric connexive system, referred to as Ps in Ferguson (²⁰¹⁵). Priest proposes his system as a way to formally incarnate the allegedly long-running conception of negation as cancellation. This account considers the negation of a given formula to erase or cancel the content of the negated formula, thereby classifying contradictions as having no content. ¹⁴

From a merely technical point of view, logical consequence in the context of Priest’s system can be defined as follows:

This already allows to state something else about the relation between our system ST^c and Priest’s P_s. Our logic is, more specifically, a non-transitive subsystem of his. This can be established either by observing the previous definitions or by inspecting the semantic definition of logical consequence for Priest’s system:

and the corresponding semantic definition for our system—unsurprisingly, a refinement of the model-theoretic definition of ST consequence discussed in the previous section.

Being a subsystem of P_s, our logic ST^c is non-reflexive and non-monotonic much as Priest’s logic. ¹⁵ This can be witnessed, in turn, by the invalidity of the following inferences.

Let us clarify the meaning of these invalidities, in terms of the inferential interpretation of ST^c. For example, at first glance one could think that if ST^c is non-reflexive, then it must be because it allows the overlap between assertion and denial, for some sentences at least. But that is not the case. In fact, the failure of Reflexivity is bound to happen because ST^c consequence includes novel ways for Reflexivity to fail other than the aforementioned overlap. As is evident from the definition of logical consequence in this fragment of ST, for Γ ⊢ST^c Δ to hold it is necessary that both the assertion of Γ, and the denial of Δ can be in bounds, taken separately. However, in the case of p∧¬p ⊢p∧¬p, and also in the case of p∨¬p ⊢p∨¬p there are formulas which do not satisfy these constraints and, thus, cannot inferentially induce a corresponding valid argument. Thus, Reflexivity cannot be accepted.

This is not to say, though, that Reflexivity must fail for all formulas, but instead only for those formulas which are not properly assertable or not properly deniable on their own—or, which is the same, only for those formulas that are not properly assertable or not properly deniable while staying within the bounds. Restricted versions of Reflexivity, concerning assertable and deniable formulas are perfectly valid in our target fragment ST^c.

The failure of Weakening can be similarly explained. One could think that, contra Ripley’s arguments, such a rejection must be due to some additional assertion and denials taking back into the bounds a position that was initially out of bounds. But that is not the case. Yet again, the failure of Weakening is bound to happen because the definition of STc consequence includes novel ways for Weakening to fail. Consider, for example, the argument p⊢p and notice that it satisfies the normal and the refined constraints for being a valid argument. In fact, if we look at the position associated to it we observe that p can be both properly asserted and, non-simultaneously, properly denied without falling out of bounds, and that asserting and denying p is out of bounds. This is not the case, however, when we move to the position associated with the argument p,¬p ⊢p. In such a case, even if p alone can be properly denied without falling out of bounds, asserting p and ¬p together pushes us immediately out of bounds. Thus, this position cannot induce a valid argument in STc. Since the transition from p⊢p to p, ¬p ⊢p can sometimes fail in our system, Weakening cannot be accepted. A similar argument can be run, substituting p,¬p ⊢p for p ⊢p,¬p in the previous sentences.

This is not to say, again, that Weakening must fail for all sets of formulas. Instead, it only fails where either asserting the premises or denying the conclusions of the conclusion position is out of bounds per se, while it is not so for the premise position. Restricted versions of Weakening not having these problems are perfectly valid in our target system ST^c.

To close this section let us highlight, though, that regardless of the technical coincidence there are also some key philosophical differences between Priest’s approach and ours. In fact, while Priest’s system is induced by the allegedly long-running conception of negation as cancellation, this has nothing to do with our motivation here. Thus, even if close cousins from a formal point of view, Priest’s account and ours differ in their philosophical parentage. Priest requires the classical satisfiability of the premises and the negation of the conclusion, for reasons related to content-theoretic constraints imposed on valid arguments. We require these additional conditions for reasons related to the relevance of the assertion of the premises and the denial of the conclusions in rendering an argument valid.

4. Conclusion

In this paper we explored a fragment of ST which can be regarded, on an inferential reading of connexivity, as a connexive logic. We arrived at such a fragment through the consideration of a set of restrictions on the bound-theoretic consequence relation defended by Ripley in Uncut and several other works.

In particular, we defended an account according to which new necessary conditions are added for an argument Γ⊢Δ to be valid. In this vein, the characteristic ST clause demanding that the corresponding position should be out of bounds is required, along with the newly introduced provisos that—taken separately—both the assertion of the premises Γ and denial of the conclusions Δ should not fall out of bounds. The analysis of the resulting system, ST_c, was accompanied with a comparison between our account and Priest’s logic P_s from Priest (^1999a), leading to prove that ours is in fact a non-transitive subsystem of P_s.

Finally, it was also remarked that under a particular reading of the informal notion of relevance which is targeted by relevant logics, the current proposal can be seen as such, for it requires that both the assertions and the denials contained in the position are properly employed in rendering the position in question out of bounds. This is not to the detriment of potential applications of the usual relevant criteria to ST. Namely, of characterizing various subsystems of ST which comply with relevant criteria discussed in e.g. Anderson and Belnap (¹⁹⁷⁵), such as those of Anderson and Belnap, or Parry. Technically speaking this could be fulfilled by considering, on the one hand, non-transitive versions of e.g. Belnap-Dunn logic FDE from Belnap (¹⁹⁷⁷), Dunn (¹⁹⁷⁶), and by considering non-transitive versions of some Parry logics like Deutsch’s system S_fde from Deutsch (¹⁹⁸⁴), on the other. We hope to explore such alternatives in the future.