Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.1 Bahía Blanca ene./mar. 2006
Stability of systems with time-varying delay
E. Slawiñski, V. A. Mut and J. F. Postigo
Instituto de Automática (INAUT). Universidad Nacional de San Juan.
Av. Libertador San Martín 1109 (oeste). J5400ARL. San Juan, Argentina.
e-mail:{slawinski, vmut, jpostigo}@inaut.unsj.edu.ar
Abstract — This paper presents a useful theoretical extension of the Lyapunov-Krasovskii's theory to analyse the exponential stability of differential equations with time-varying delay. The presented theoretical analysis allows establishing the coefficients of an upper exponential bound of the real response of a delayed system. In addition, we propose stability conditions -delay amplitude independent- applied to linear and non-linear systems with time-varying delay. Based on the Krasovskii-type functional, the proposed functionals incorporate information of the delayed system. The main motivation of this paper is to arrive at conditions of exponential stability that show directly the influence of the time-varying delay and the non-delayed dynamics on the real response of a delayed system. Theoretical results are tested through a numerical example.
Keywords — Delayed Systems. Exponential Stability. Linear Systems. Non-Linear Systems. Time-Varying Delay.
I. INTRODUCTION
Many real systems are represented by delayed differential equations, with models applied to biology, chemistry, economics, mechanics, medicine, physics, etc. (Hale and Lunel, 1993; Kolmanovskii and Myshkis, 1999). In general, the introduction of a time delay into the differential equations may lead to instability or to a bad performance of the system (Kolmanovskii and Myshkis, 1992; Niculescu, 2001; Richard, 2003). On the other hand, the literature presents various criteria to analyse the stability of non-linear and linear systems with time delay (Kharitonov, 1999; Kolmanovskii et al., 1998 and 1999b). Main stability conditions are based on the Lyapunov-Krasovskii functional (Mao, 1996; Verriest and Niculescu 1997; Verriest and Aggoune, 1998; Tchangani et al., 1998; Kolmanovskii et al., 1999a; Niculescu and Mazenc, 2001; Jafarov, 2001; Nian, 2003; Han, 2004; Pepe, 2005); matrix measures norm (Mori, 1985, Niculescu et al., 1995); and Razumikhin functions (Jankovic, 1999; Teel, 1998), but these papers don't analyse how to modify the transitory of the system, which is useful for the design and control of real systems. The general purpose of this paper is to analyse the exponential stability of systems with time-varying delay studying how some factors (for example, time delay) establish the stability regions and modify the response of such systems.
Based on the Lyapunov-Krasovskii's theory applied to delayed differential equations and the Lyapunov's theory applied to differential equations, we propose a useful theoretical extension to analyse the exponential stability of delayed differential equations establishing an upper bound of the real response of a delayed system. In addition, we propose sufficient conditions -independent of the delay amplitude- to analyse the exponential stability of linear and non-linear systems with time-varying delay. In general, the used functionals are based on the Krasovskii-type functional and they depend on setting positive definite symmetric matrices in the form of Riccati equations, which are generally set by trial and error. In this work, the proposed functionals incorporate information of the delayed system arriving at useful stability conditions for control of systems. Such conditions show the influence of the time-varying delay and the non-delayed dynamics (which can be generally handled) on the stability and response of a delayed system. The paper also includes a numerical example that helps the reader to test the reached theoretical results.
The paper is organized as follows. Section II gives the notation used in this paper. In section III some background materials on delayed differential equations and the Lyapunov-Krasovskii's theory are introduced. Section IV presents the proof of the proposed main theorem for exponential stability of systems with time-varying delay. The proposed conditions of exponential stability applied to linear and non-linear systems with time varying delay are proven in section V. In addition, the stability region is analysed. Section VI presents a numerical example to verify the reached theoretical results. Finally, general conclusions are given in section VII.
II. NOTATION
In this paper, the following notation is used: h(t) ∈ ℜ+ denotes the time delay. We assume that the delay is finite and 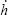 (t) < 1. Here, x(t) ∈ ℜn and |x| is the Euclidean norm of x. If B is a matrix or vector then BT is the transpose of B, |A| denotes the Euclidean norm of A ∈ ℜn×n defined by
(t) < 1. Here, x(t) ∈ ℜn and |x| is the Euclidean norm of x. If B is a matrix or vector then BT is the transpose of B, |A| denotes the Euclidean norm of A ∈ ℜn×n defined by 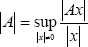 , μ(A) denotes the matrix measure (derived from the Euclidean norm) of the real matrix A computed as
, μ(A) denotes the matrix measure (derived from the Euclidean norm) of the real matrix A computed as 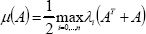 , where λi(AT + A) are the eigenvalues of AT + A. On the other hand, xt (for a given time instant t) is the function defined by xt(θ) = x(t+θ) for θ ∈ [-h(t),0] , for example: xt(0) = x(t), xt(-h) = x(t - h); and the norm ||.|| is defined by
, where λi(AT + A) are the eigenvalues of AT + A. On the other hand, xt (for a given time instant t) is the function defined by xt(θ) = x(t+θ) for θ ∈ [-h(t),0] , for example: xt(0) = x(t), xt(-h) = x(t - h); and the norm ||.|| is defined by 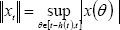 . Here, (C, ||.||) is the Banach space of continuous functions on the interval [t-h(t),t] at any time t, and CH:= {ψ ∈ C: ||ψ|| ≤ H}. On the other hand, given a non-linear differentiable function
. Here, (C, ||.||) is the Banach space of continuous functions on the interval [t-h(t),t] at any time t, and CH:= {ψ ∈ C: ||ψ|| ≤ H}. On the other hand, given a non-linear differentiable function 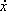 (t) = g(x(t),x(t - h)), the incremental gain of g is defined as |g| = inf{γ:|g(x1,x2)-g(y1,y2)| ≤ γ |[x1 x2] - [y1 y2]|} ∀ x1, x2, y1, y2 ∈ ℜn.
(t) = g(x(t),x(t - h)), the incremental gain of g is defined as |g| = inf{γ:|g(x1,x2)-g(y1,y2)| ≤ γ |[x1 x2] - [y1 y2]|} ∀ x1, x2, y1, y2 ∈ ℜn.
III. STABILITY OF DELAYED SYSTEMS
Let's consider the delayed functional differential equation given by,
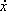 (t) = f(t,xt), (1)
(t) = f(t,xt), (1)
where x ∈ ℜn, xt ∈ C, t, t0 ∈ ℜ+, and f:ℜ+×C→ℜn with f(t,0) = 0, ∀t ≥ t0. Here, f is continuous and takes bounded sets into bounded sets. We assume that there exists a solution x(t;t0,ψ0) of (1) which depends continuously on the initial data [t0,ψ0], where ψ0 = x(t0 + θ) for θ ∈ [-h(t0),0] with ψ0 ∈ CH. Sufficient conditions implying existence, uniqueness and continuous dependence can be found in the standard theory (e.g., Driver, 1962, Sawano, 1982 and Burton, 1985 ). From now on, we will denote the solution norm by |x(t;t0,ψ0)| = |xt(0)|.
The transition from x to xt is shown in Fig. 1 for an arbitrary example with h(t1) > h(t0). The right hand side of (1) is a function of t, and a functional of xt, i.e. to any t and any function ψt ∈ C corresponds a vector f(t,ψt) ∈ ℜn.
The following definitions and facts are a standard in the theory of delayed functional differential equations (Bellman and Cooke, 1963; Krasovskii, 1963; Hale, 1977; Hale and Lunel, 1993; Kolmanovskii and Myshkis, 1992; Kolmanovskii and Myshkis, 1999).
Definition 1. The solution xt = 0 of (1) is said to be asymptotically stable if,
a) For every ε > 0 and each t0 ≥ 0 there exists ρ = ρ(ε,t0) such that ||ψ0|| < ρ implies that |x(t;t0,ψ0) < ε| for all t0 ≥ 0.
b) For every t0 ≥ 0 there exists ε1 = ε1(t0) such that if ||ψ0|| < ε1, then |x(t;t0,ψ0)|→0 as t→∞.
If ρ and ε1 are independent from the initial time t0, then the zero-solution is uniformly asymptotically stable.
Definition 2. The solution xt = 0 of (1) is called exponentially stable if there exist constants γ > 0 and α > 0, such that every solution of (1) satisfies the following condition:
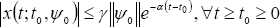 , (2)
, (2)
Fact 1 (Lyapunov, 1949). Applying the Lyapunov's theory of differential equations to delayed differential equations described by (1) it is easy to arrive at a sufficient condition of exponential stability given by:
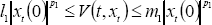 , (3)
, (3)
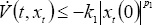 , (4)
, (4)
or
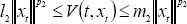 , (5)
, (5)
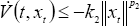 , (6)
, (6)
where the functional V : ℜ+ × C → ℜ+ maps bounded sets of C into bounded sets of ℜ+, 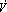 (t,xt) is the time derivative of V(t, xt) along the trajectories of (1) , the coefficients l1, m1, l1, k1, l2, m2, l2 ∈ ℜ+ and p1, p2 are positive integers.
(t,xt) is the time derivative of V(t, xt) along the trajectories of (1) , the coefficients l1, m1, l1, k1, l2, m2, l2 ∈ ℜ+ and p1, p2 are positive integers.
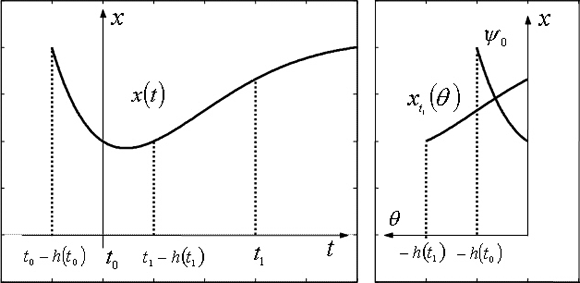
Figure 1. Transition from x(left) to xt(right).
The solution of the system has an upper bound defined by 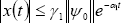 , where
, where 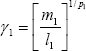 and
and 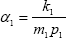 -from (3) and (4)- or
-from (3) and (4)- or 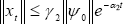 , where
, where 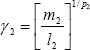 and
and 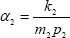 -from (5) and (6)-. The coefficients γ1, α1 or γ2, α2 are computed as the Lyapunov's classical coefficients.
-from (5) and (6)-. The coefficients γ1, α1 or γ2, α2 are computed as the Lyapunov's classical coefficients.
The practical problem of this theorem applied to delayed differential equations is to find any functional to easily compute the coefficients l1, m1, k1 or l2, m2, k2 that define the exponential upper bound of the system real response. In general, the used functionals are based on the Krasovskii-type functional (Richard, 2003). The classical Krasovskii functional for systems with time varying delay is given by:
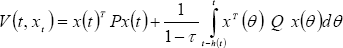 | (7) |
where P, Q are positive definite matrices, h(t) is the time delay and 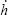 (t) < τ <1, with τ ∈ (-∞,1).
(t) < τ <1, with τ ∈ (-∞,1).
Fact 2 (Krasovskii, 1963). Let's suppose that the function f : ℜ+ × C → ℜn maps bounded sets of C into bounded sets of ℜn, and that u(s), v(s) and w(s) are scalar, continuous, positive and non-decreasing functions. If there exists a continuous functional V : ℜ+ × C → ℜ+, and the following conditions hold:
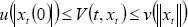 , (8)
, (8)
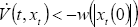 , (9)
, (9)
where 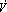 is the time-derivative of V(t, xt) along the trajectories of (1); then the solution xt = 0 is uniformly asymptotically stable.
is the time-derivative of V(t, xt) along the trajectories of (1); then the solution xt = 0 is uniformly asymptotically stable.
This theorem allows using the Krasovskii-type functional (7), however only conditions of asymptotic stability are achieved, which for many applications is not accepted.
IV. EXPONENTIAL STABILITY OF SYSTEMS WITH TIME-VARYING DELAY
This section presents the main contribution of this paper. Based on the Lyapunov-Krasovskii's theory applied to delayed differential equations and the classical Lyapunov's theory applied to differential equations, we propose a useful theoretical extension to analyse the exponential stability of delayed differential equations establishing an upper bound (which can be easily computed using Krasovskii-type functionals as will be presented in section VI) for the real response of the delayed system.
Theorem 1. The zero solution of the delayed system 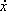 = f(t,xt) (f is supposed to map bounded sets of C into bounded sets of ℜn and the time delay is bounded by
= f(t,xt) (f is supposed to map bounded sets of C into bounded sets of ℜn and the time delay is bounded by 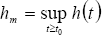 ) is exponentially stable if there exists a differentiable functional V : ℜ+ × C → ℜ+, and the following conditions hold,
) is exponentially stable if there exists a differentiable functional V : ℜ+ × C → ℜ+, and the following conditions hold,
a|xt(0)|p ≤ V(t,xt) ≤ b||xt||p, (10)
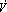 (t,xt) ≤ -c|xt(0)|p, (11)
(t,xt) ≤ -c|xt(0)|p, (11)
where a, b, c are positive constants, p is a positive integer and 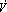 (t,xt) is the time derivative of V(t, xt) along the system trajectories (1). The solution of the system has an upper bound defined by
(t,xt) is the time derivative of V(t, xt) along the system trajectories (1). The solution of the system has an upper bound defined by 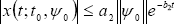 , ∀t ≥ t0 ≥ 0, where,
, ∀t ≥ t0 ≥ 0, where, 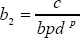 ,
, 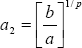 and d is the solution of
and d is the solution of 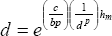 .
.
Proof. This theorem is motivated on the classical Lyapunov and Krasovskii theories for differential equations and delayed differential equations, respectively.
From (11), we can express the following:
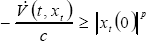 | (12) |
Now, from (10) we obtain that,
V(t,xt) ≤ b||xt||p. (13)
We suppose that there exists a constant d > 0 such that ∀|xt(0)| ≠ 0 verifies the following:
||xt||p ≤ dp|xt(0)|p. (14)
We will prove (14) by reductio ad absurdum: If (14) is false, then ||xt||p > dp|xt(0)|p ∀d > 0. Now, if d → ∞ then ||xt|| → ∞ ∀t ≥ t0, which is absurd because we assume that the initial condition ψ0 is bounded, i.e. ||ψ0|| ∈ CH (see Section III). Therefore, we can assure that there exists at least a constant d which verifies (14). From (13) and (14),
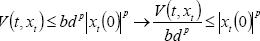 | . (15) |
Since (12) and (15), we can write the following:
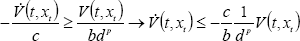 | . (16) |
The solution for (16) is an exponential function as follows:
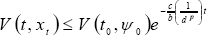 | , (17) |
where we set t0 = 0 only for simplicity.
Next, from (10) and (17), it yields,
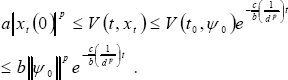 | (18) |
Then, by obtaining |xt(0)| from (18),
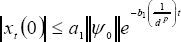 | , (19) |
where the coefficients a1, b1 of (19) are the Lyapunov's classical coefficient for exponential stability, that is:
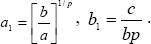 | (20) |
From (19), and because the exponential function is continuously decreasing, it holds that,
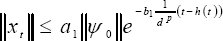 | . (21) |
Fig. 2 shows graphically the qualitative relation between the bounds of |xt(0)| and xt(θ), with θ ∈ [-h(t),0].
Now, from (14) and (19), we can express the following:
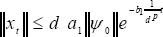 | . (22) |
On the other hand, we can re-write (21) as follows:
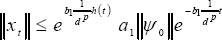 | . (23) |
By comparing (22) and (23), we verify that d exist and it is the solution of,
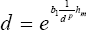 | (24) |
where 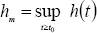 . The functions -dependent on d- in left and right hand of (24) are increasing and decreasing functions, respectively. Then it will always exist solution for d. Figure 3 shows an example for three values of hm, where b1 = 1. The higher the maximum time delay hm, the higher d is.
. The functions -dependent on d- in left and right hand of (24) are increasing and decreasing functions, respectively. Then it will always exist solution for d. Figure 3 shows an example for three values of hm, where b1 = 1. The higher the maximum time delay hm, the higher d is.
Finally, the inequality (19) can be expressed as (2),
|x(t;t0,ψ0)| ≤ γ||ψ0||e-αt, (25)
where:
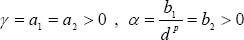 | . (26) |
From (25) and (26), Theorem 1 is proven. The inequality (25) satisfies definition 2 of exponential stability. ∆
The proposed Theorem 1 is a useful theoretical extension of the Lyapunov-Krasovskii's theory for exponential stability of delayed differential equations. From (24), the higher the maximum time delay hm, the higher d is and therefore, the lower the exponential rate α1 -from (26)- of the upper bound of the system response will be. The coefficients of the upper exponential bound -for the real response of the delayed system- are easily computed for delayed linear systems, as will be analysed in the section VI through a numerical example.
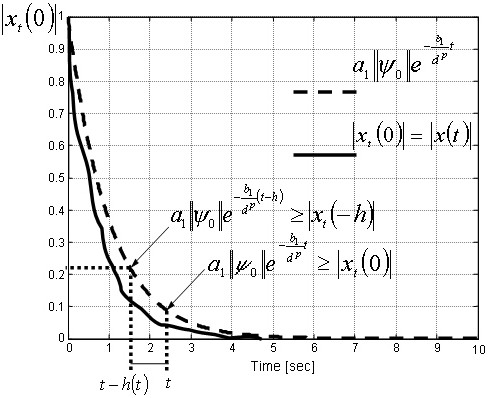
Figure 2. Evolution of the upper bound of |xt(0)|.
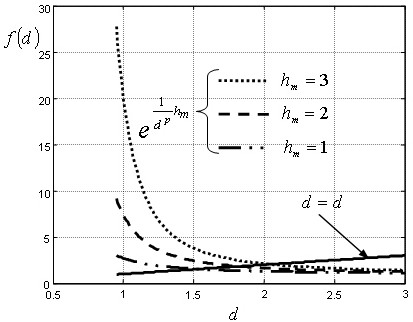
Figure 3. Relation between d and hm.
V. STABILITY CONDITIONS OF SYSTEMS WITH TIME-VARYING DELAY
In this section, we propose conditions of exponential stability applied to linear (Section A) and non-linear (Sections B and C) systems with time varying delay. Our contribution in this section is the way to build a functional, which incorporates information of the delayed system. In addition, we will analyse the achieved stability region, which will depend on the maximum derivative of the time delay and the non-delayed dynamics of the system.
A. Stability of linear systems with time-varying delay
Let us consider a delayed linear system described by,
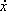 (t) = Ax(t) + Bx(t - h(t)), (27)
(t) = Ax(t) + Bx(t - h(t)), (27)
where A, B ∈ ℜn×n, x(t) ∈ ℜn, and 0 ≤ h(t) ≤ hm ∈ ℜ+, 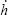 (t) < τ < 1, ∀t ≥ t0, with τ ∈ (-∞,1).
(t) < τ < 1, ∀t ≥ t0, with τ ∈ (-∞,1).
Theorem 2. The zero solution of the delayed system described by (27) is exponentially stable if,
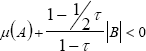 | (28) |
where |B| is the Euclidean norm of the matrix B, μ(A) is the matrix measure of the matrix A and the time-derivative of the delay verifies that 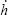 (t) < τ < 1.
(t) < τ < 1.
Proof: A functional V : ℜ+ × C → ℜ+ based on Lyapunov-Krasovskii's theory is proposed as follows:
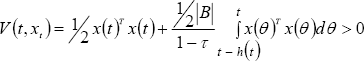 | , (29) |
where the proposed functional incorporates information of the delayed dynamics (|B|).
From (29) and considering that the delay h(t) is bounded (h(t) ≤ hm) and that xT x = |xt(0)|2 ≤ ||xt||2 (by using norm properties), then the proposed functional V(t, xt) verifies condition (10) - given by Theorem 1-,
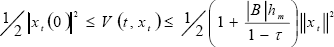 | , (30) |
where the values a, b, p obtained by comparing (10) and (30) are the following:
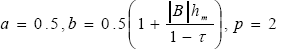 | . (31) |
The derivative of V(t,xt) along the system trajectories (27) is,
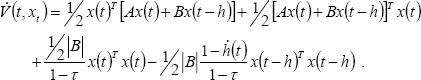
By re-arranging terms and considering that x(t)T Bx (t - h(t)) = [x(t)T Bx (t - h(t))]T because it is a real number (B ∈ ℜn×n, x ∈ ℜn), then,
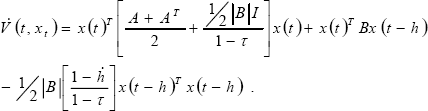
where I ∈ ℜn×n is the identity matrix. Using the inequality 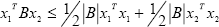 into
into 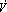 (t,xt), with x1 = x(t) and x2 = x(t - h), it follows that,
(t,xt), with x1 = x(t) and x2 = x(t - h), it follows that,
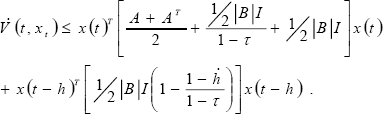
We use the property of the matrix measure given by x(t)T 0.5[A + AT]x(t) ≤ x(t)T [μ(A)I]x(t) into 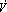 (t,xt) as follows,
(t,xt) as follows,
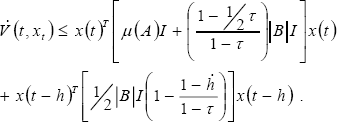 | (32) |
The second term of the right hand in (32) is negative definite because 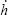 (t) < τ <1. From (32), condition (11) –given by Theorem 1- is satisfied if (28) is verified. Therefore, inequalities (30) and (32) satisfy the stability conditions required by Theorem 1, and in consequence, the origin of the system (27) is exponentially stable. ∆
(t) < τ <1. From (32), condition (11) –given by Theorem 1- is satisfied if (28) is verified. Therefore, inequalities (30) and (32) satisfy the stability conditions required by Theorem 1, and in consequence, the origin of the system (27) is exponentially stable. ∆
Next, we apply the property of the matrix measure given by Re λi(X) ≤ μ(X) into (28) as follows:
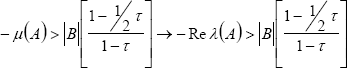 | . (33) |
Figure 4 shows the influence of the maximum derivative of the time delay on the stability region -given by (33)- for two arbitrary values |B| = 1 and |B| = 2.
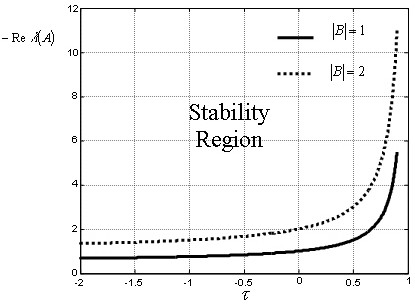
Figure 4. Stability region as a function of τ.
The achieved stability condition (33) is independent of the delay amplitude and it depends on three main factors: the real part of the eigenvalues Reλ(A) of the non-delayed dynamics of the system, the norm |B| of the delayed dynamics of the system and the maximum time-derivative τ of the time delay. Moreover, the greater the time derivative of the time delay (τ), the stronger the stability of the non-delayed system (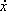 = Ax) to reach the stability of the system with time delay.
= Ax) to reach the stability of the system with time delay.
B. Stability of delayed linear systems with nonlinear components
Let us consider a delayed linear system described by,
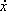 (t) = Ax(t) + Bx(t - h(t)) + f(x(t)) + g(x(t - h(t))), (34)
(t) = Ax(t) + Bx(t - h(t)) + f(x(t)) + g(x(t - h(t))), (34)
where A, B ∈ ℜn×n, x(t) ∈ ℜn and 0 ≤ h(t) ≤ hm ∈ ℜ+, 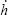 (t) < τ < 1, ∀t ≥ t0, with τ ∈ (-∞,1). It is assumed that the non-linear functions f and g belong to a class of functions Ω : ℜn → ℜn satisfying ∀θ ∈ Ω (Verriest and Aggoune, 1998),
(t) < τ < 1, ∀t ≥ t0, with τ ∈ (-∞,1). It is assumed that the non-linear functions f and g belong to a class of functions Ω : ℜn → ℜn satisfying ∀θ ∈ Ω (Verriest and Aggoune, 1998),
| θ(0) = 0, ∀t and | 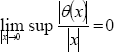 | . (35) |
Condition (35) ensures that for perturbations f(x) and g(x) in class Ω, there exist kf, kg, η > 0, such that ∀|x| < η,
|f(x)| ≤ kf|x|, (36)
|g(x)| ≤ kg|x|. (37)
Theorem 3. The zero solution of the delayed system represented by (34) is locally exponentially stable if :
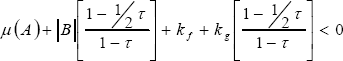 | . (38) |
Proof. A functional V : ℜ+ × C → ℜ+ is proposed as follows:
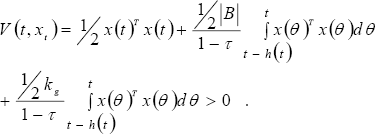 | (39) |
where the proposed functional incorporates information of the delayed dynamics (|B| and kg).
From (39) and considering that the delay h(t) is bounded (h(t) ≤ hm) and xT x = |xt(0)|2 ≤ ||xt||2 (by using norm properties), then the proposed functional V(t,xt) verifies condition (10) –given by Theorem 1-,
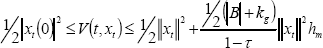 | . (40) |
The time-derivative of V(t, xt) along the system trajectories (34) is similar to (32), but with the addition of four new terms as follows,
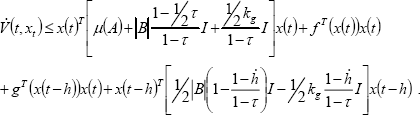 | (41) |
From (36), (37), and by using norm properties, the following inequalities are obtained,
f(x(t))T x(t) ≤ |f(x(t))||x(t)| ≤ kf x(t)T x(t), (42)
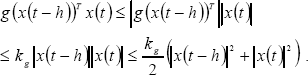 | (43) |
Substituting (42) and (43) in (41), it yields,
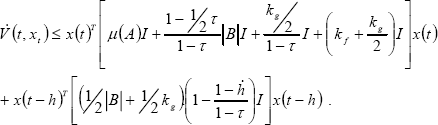
Now, by re-arranging terms into 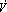 (t,xt), we can express the following,
(t,xt), we can express the following,
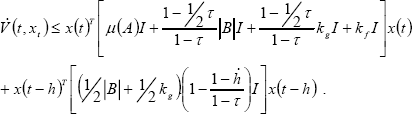 | (44) |
The second term of the right hand in (44) is negative definite because 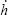 (t) < τ < 1. From (44), condition (11) -Theorem 1- is satisfied if (38) is verified. Therefore, inequalities (40) and (44) satisfy the stability conditions required by Theorem 1, and in consequence, the origin of the system (34) is locally exponentially stable. ∆
(t) < τ < 1. From (44), condition (11) -Theorem 1- is satisfied if (38) is verified. Therefore, inequalities (40) and (44) satisfy the stability conditions required by Theorem 1, and in consequence, the origin of the system (34) is locally exponentially stable. ∆
The stability condition (38) clearly shows the effect of the delayed and non-delayed non-linearity on the system behaviour. The influence on the system stability of the delayed dynamics (linear or non-linear) depends on the maximum time-derivative of the time delay.
C. Stability of nonlinear systems with time-varying delay
Let us consider a non-linear system with time varying delay described by,
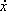 (t) = f(x(t)) + g(x(t),x(t - h)), (45)
(t) = f(x(t)) + g(x(t),x(t - h)), (45)
where 0 ≤ h(t) ≤ hm and 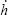 (t) < τ < 1, with hm ∈ ℜ+, x ∈ ℜn, t, t0 ∈ ℜ+, f:ℜn → ℜn and g:ℜn × ℜn → ℜn, with f(0) = 0 and g(0,0) = 0 ∀t ≥ t0. In addition, we assume that f and g map bounded sets (ℜn and ℜn × ℜn, respectively) into bounded sets in ℜn.
(t) < τ < 1, with hm ∈ ℜ+, x ∈ ℜn, t, t0 ∈ ℜ+, f:ℜn → ℜn and g:ℜn × ℜn → ℜn, with f(0) = 0 and g(0,0) = 0 ∀t ≥ t0. In addition, we assume that f and g map bounded sets (ℜn and ℜn × ℜn, respectively) into bounded sets in ℜn.
Lemma 1. If a system represented by 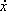 = f(x) is exponentially stable, then there exist α, λ ∈ ℜ+ such that xT f(x) ≤ -λxTx, where |x| ≤ α|x(0)|e-λt.
= f(x) is exponentially stable, then there exist α, λ ∈ ℜ+ such that xT f(x) ≤ -λxTx, where |x| ≤ α|x(0)|e-λt.
Proof. If the system 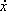 = f(x) is exponentially stable, then it satisfies that |x| ≤ α|x(0)|e-λt, and therefore:
= f(x) is exponentially stable, then it satisfies that |x| ≤ α|x(0)|e-λt, and therefore:
x ≤ α|x(0)|e-λtI1. (46)
where I1 ∈ ℜn with I1(i,1) = 1 for 0 < i ≤ n. From (46), the evolution of 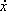 verifies that,
verifies that,
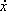 ≤ -λα|x(0)|e-λtI1. (47) .
≤ -λα|x(0)|e-λtI1. (47) .
Using (46) and (47) on -λxTx, the following can be expressed:
-λxT x≤ -λ(α|x(0)|e-λt)(α|x(0)|e-λt) ≥ xT 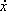 = xT = f(x). (48)
= xT = f(x). (48)
Inequality (48) proves the proposed Lemma. ∆
Theorem 4. Let us suppose that the subsystem 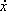 = f(x) of the system (45) is exponentially stable with rate λ, then the following condition ensures the exponential stability of the system (45):
= f(x) of the system (45) is exponentially stable with rate λ, then the following condition ensures the exponential stability of the system (45):
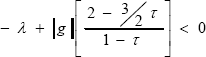 | , (49) |
where λ, |g| ∈ ℜ+ and 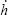 (t) < τ < 1. The norm |g| is the incremental gain of the function g(.).
(t) < τ < 1. The norm |g| is the incremental gain of the function g(.).
Proof. A functional V : ℜ+ × C → ℜ+ is proposed as follows,
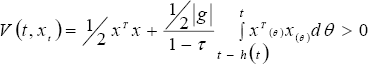 | , (50) |
where the proposed functional incorporates information of the delayed dynamics (|g|).
From (50) and considering that the delay h(t) is bounded (h(t) ≤ hm) and that xT x = |xt(0)|2 ≤ ||xt||2 (by using norm properties), then the proposed functional V(t, xt) verifies condition (10) -given by Theorem 1-,
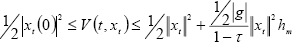 | . (51) |
where the values a, b, p comparing (10) and (51) are the following:
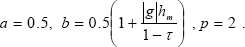
The time-derivative of V(t, xt) along the system trajectories (45) is,
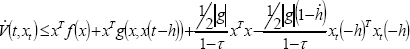 | (52) |
Now, the following inequalities are attained using norm properties,
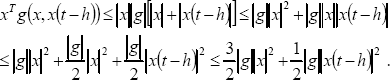 | (53) |
Introducing (53) into (52), it yields,
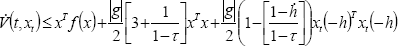 | . (54) |
The third term of the right hand in (54) is negative definite because 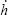 < τ < 1. By applying Lemma 1 to (54) and organizing terms, it yields,
< τ < 1. By applying Lemma 1 to (54) and organizing terms, it yields,
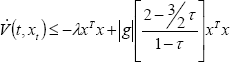 | . (55) |
From (55), condition (11) –given by Theorem 1- is satisfied if,
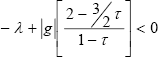 | . (56) |
Inequalities (51) and (56) verify the stability conditions given by Theorem 1 –inequalities (10) and (11)-. In addition, we remark that (56) is equal to (49). Therefore, the proposed Theorem 4 is proven ensuring the exponential stability of the system (45). ∆
Figure 5 shows the influence of the maximum derivative of the time delay on the stability region -given by (56)- for three arbitrary values |g| = 0.5, |g| = 1 and |g| = 2. The achieved stability condition is independent of the delay amplitude and it depends on three main factors: the exponential rate λ of the non-delayed system 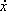 = f(x), the norm |g| of the delayed non-linear function g(x,x(t - h)) and the maximum time-derivative τ of the time delay. Then, we can conclude that the greater the temporal derivative of the time delay (τ), the stronger the stability (higher λ) of the non-delayed system (
= f(x), the norm |g| of the delayed non-linear function g(x,x(t - h)) and the maximum time-derivative τ of the time delay. Then, we can conclude that the greater the temporal derivative of the time delay (τ), the stronger the stability (higher λ) of the non-delayed system (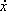 = f(x)) to reach the stability of the system with time delay. In addition, if |g| → 0 then the proposed stability condition tends to the stability condition of a non-delayed system, this is: λ < 0.
= f(x)) to reach the stability of the system with time delay. In addition, if |g| → 0 then the proposed stability condition tends to the stability condition of a non-delayed system, this is: λ < 0.
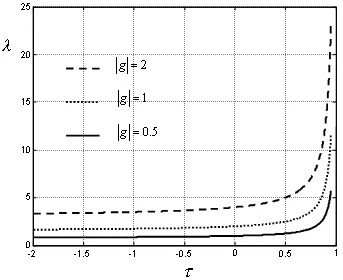
Figure 5. Stability region in function of τ.
VI. NUMERICAL EXAMPLE
In this section, we present a numerical example of a linear system with time-varying delay. The objective of this example is to verify numerically the achieved theoretical results through the simulation of systems with time-varying delay.
Let us consider the system given by (27) with scalar values A = A, B = 1. The initial condition is xt(θ) = 1 for θ ∈ [-h(t0),0] and the time delay is represented by h(t) = 0.1t[sec.], then τ = 0.1. From Theorem 2 (28), the stability condition on A is,
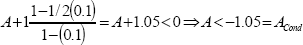 | (57) |
By regarding h(t) = 0.5t[sec.] (τ = 0.5) in the above system, the stability condition becomes,
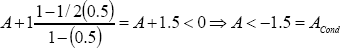 | (58) |
Figures 6 and 7 show the state evolution x(t) of the example systems for several values of A. If the stability condition given by Theorem 2 (28) is satisfied –conditions on A given by (57) and (58)-, then x(t) → 0 with exponential rate, in spite of the several values of the time-varying delay. Moreover, the higher the time-derivative of the delay, the stronger the stability of the non-delayed dynamics of the system (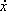 = Ax) to assure the stability of the delayed system. The simulations of the delayed system verify the achieved theoretical result given by Theorem 2.
= Ax) to assure the stability of the delayed system. The simulations of the delayed system verify the achieved theoretical result given by Theorem 2.
Now, we consider a time delay represented by: h(t) = 0.1t + 0.5[sec.] for 0 ≤ t ≤ 5[sec.], and h(t) = 1[sec.] for t ≥ 5[sec.], then hm = 1[sec.]. In addition, we set A = -2. From Theorem 1 and Theorem 2, the upper bound of the response of the system with time-varying delays may be computed –by considering that the main transitory of the system is on the time-interval t < 5[sec.], then τ = 0.1 -. From (28) and (30) –Theorem 2-, it yields,
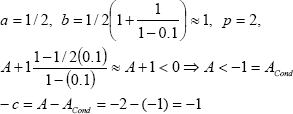 | (59) |
From Theorem 1 -by using a, b, c, p from (59)-, we compute a2, b2 as follows:
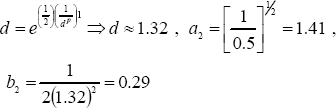 | (60) |
The resulting coefficients in (60) are used by Theorem 1 to compute the theoretical upper bound of the norm of x(t) as |x(t)| ≤ 1.41||ψ0||e-0.29t. Fig. 8 shows the simulated response of |xt(0)|,|xt(-h)| and the theoretical upper bound of |x(t)|.
The theoretical upper bound is useful as a performance measure for the analysis and design of control systems. In addition, the example has shown that the theoretical upper bound can be easily computed for delayed linear systems.
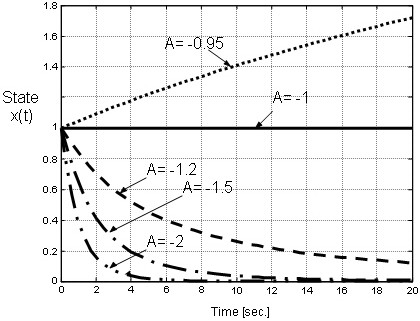
Figure 6. Evolution of the state x(t) for τ = 0.1.
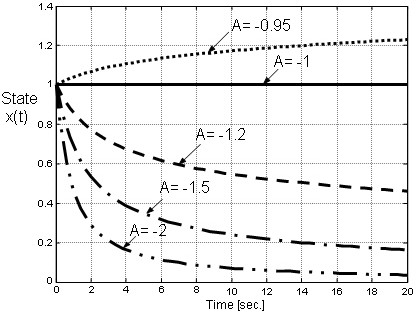
Figure 7. Evolution of the state x(t) for τ = 0.5.
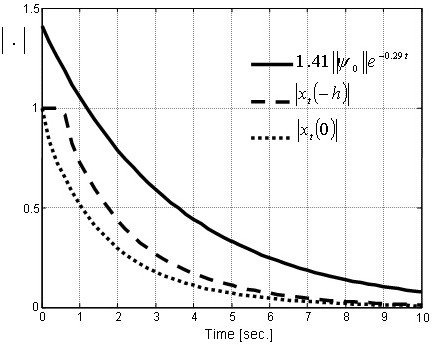
Figure 8. Upper bound of the system response.
VII. CONCLUSIONS
In this paper it has been proposed a useful theoretical extension to analyse the exponential stability of delayed differential equations establishing an upper bound for the real response of a delayed system. In addition, conditions of exponential stability for linear and non-linear systems with time-varying delay were proposed and the analysis of the achieved regions of stability was also presented.
The proposed stability conditions depend on the maximum derivative of the time delay, but they are independent of the delay amplitude. The higher the time-derivative of the time delay, the stronger the stability of the non-delayed dynamics of the system to ensure the exponential stability of the delayed system. The main utility of the achieved conditions of exponential stability is that they directly depend on the non-delayed dynamics of the system (which can be generally handled or controlled) and the maximum derivative of the time delay (which can be generally measured in line).
On the other hand, the presented theoretical analysis allows setting the coefficients of an exponential response that bounds the system real response. Such coefficients can be easily computed as shown the presented numerical example (for a delayed linear system) and they are a performance measure of the system, which is useful to analyse and design control strategies for delayed systems. Finally, the simulation results were satisfactory, verifying the achieved theoretical results.
ACKNOWLEDGMENT
This work was partially funded by the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina.
REFERENCES
1. Bellman, R.E. and K.L. Cooke, "Differential-Difference Equations", Academic Press, New York (1963). [ Links ]
2. Burton T.A., "Stability and Periodic Solutions of Ordinary and Functional Differential Equations", Mathematics in Science and Engineering, 178, Academic Press (1985). [ Links ]
3. Driver, R.D., "Existence and Stability of Solutions of a Delay-Differential System", Arch. Rational Mech. Anal., 10, 401-426 (1962). [ Links ]
4. Hale J.K., "Theory of Functional Differential Equations", Springer Verlag, New York (1977). [ Links ]
5. Hale J.K. and V. Lunel, "Introduction to Functional Differential Equations", Springer, New York (1993). [ Links ]
6. Han Q.-L., "On robust stability of neutral systems with time-varying discrete delay and norm-bounded uncertainty", Automatica, 40, 1087-1092 (2004). [ Links ]
7. Jafarov E., "Comparative Analysis of Simple Improved Delay-Dependent Stability Criterions for Linear Time-Delay Systems: An Augmented Functional Approach", Proc. of the American Control Conference, Arlington, VA June 25-27, 3389-3394 (2001). [ Links ]
8. Jankovic M., "Control Lyapunov-Razumikhin functions for time-delay systems", Proc. 38th IEEE Conf. Decision and Control, 1136-1141 (1999). [ Links ]
9. Kharitonov V.L., "Robust stability of time delay systems: a survey", Annual Reviews in Control, 23, 185-196 (1999). [ Links ]
10. Kolmanovskii, V.B., and A.D. Myshkis, "Applied Theory of functional differential equations", Kluwer Academic Publishers, Dordrecht, The Netherlands (1992). [ Links ]
11. Kolmanovskii V. B., S. Niculescu and J.P. Richard, "Some Remarks on the Stability of Linear Systems with Delayed State", Proc. 37th IEEE Conf. Decision and Control, 299-304 (1998). [ Links ]
12. Kolmanovskii, V.B., and A.D. Myshkis, "Introduction to the theory and applications of functional differential equations", Kluwer Academic Publishers, Dordrecht, The Netherlands (1999). [ Links ]
13. Kolmanovskii V. B., S. Niculescu and J.P. Richard, "On the Lyapunov–Krasovskii functional for stability analysis of linear delay systems", International Journal Control, 72 374-384 (1999a). [ Links ]
14. Kolmanovskii V. B., S. Niculescu and K. Gu, "Delay Effects on Stability: a Survey", Proc. 38th IEEE Conf. Decision and Control, 1993-1998, Phoenix, Arizona, USA (1999b). [ Links ]
15. Krasovskii, N. N., "Stability of Motion", Stanford University Press (1963). [ Links ]
16. Lyapunov, A.M., "Problème Generale de la Stabilité du Mouvement", Princeton University Press, Princeton, N.J. (1949). [ Links ]
17. Mao, X., "Exponential stability of nonlinear differential equations", Systems and Control Letters 28, 159-165 (1996). [ Links ]
18. Mori, T., "Criteria of asymptotic stability of linear time-delay systems", IEEE Trans. Automat. Control, AC- 30, 158-160 (1985). [ Links ]
19. Nian, X., "Stability of linear systems with time varying delays: A Lyapunov Functional Approach", Proc. of the American Control Conference, Denver, Colorado, USA (2003). [ Links ]
20. Niculescu S.I., C.E. De Souza, J.M. Dion and L. Dugar, "Robust exponential stability of uncertain linear systems with time-varying delays", Proc. 3rd European Control Conf., Rome, 1802-1807 (1995). [ Links ]
21. Niculescu, S.I., "Delay Effects on Stability", Springer Verlag, New York (2001). [ Links ]
22. Niculescu, S. and F. Mazenc, "Lyapunov Analysis for Nonlinear Delay Systems", Systems and Control Letters 42, 245-251 (2001). [ Links ]
23. Pepe P., "On the asymptotic stability of coupled delay differential and continuous difference equations", Automatica 41, 107-112 (2005). [ Links ]
24. Richard, J.P., "Time-delay systems: an overview of some recent advances and open problems", Automatica 39, 1667-1694 (2003). [ Links ]
25. Sawano, K., "Some Considerations on the Fundamental Theorems for Functional Differential Equations with Infinite Delay", Funkcalaj Ekvacioj 25, 97-104 (1982). [ Links ]
26. Tchangani A.P., M. Dambrine, J.P. Richard, and V.B. Kolmanovskii, "Stability of nonlinear differential equations with distributed delay", Nonlinear Analysis 34, 1081-1095 (1998). [ Links ]
27. Teel A. R., "Connection between Razumikhin-type theorems and the ISS nonlinear small gain theorem", IEEE Trans. Automat. Control, 43, 960-964 (1998). [ Links ]
28. Verriest, E. I. and S.I. Niculescu, "Delay-independent stability of linear neutral systems: A Riccati equations approach", Stability and Control of Time-delay Systems (L. Dugard and E.I. Verriest, Eds.), London: Springer-Verlag, 92-100, (1997). [ Links ]
29. Verriest E. I. and W. Aggoune, "Stability of nonlinear differential delay equations", Mathematics and Computers in Simulation 45, 257-267, (1998). [ Links ]